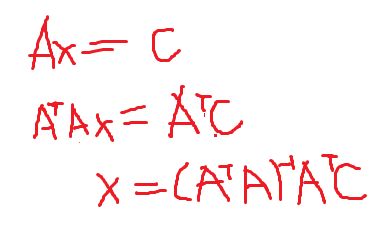最小二乘法解决的问题:Ax=C 无解下的最优解
例子1:
一条过原点的直线OA,C是直线外一点,求C在OA上的投影点P
例子2:
已知三个不在一条直线上的点A,B,C,求一条直线,使A,B,C到直线的距离和最小
例子3:
已知三个不在一条直线上的点A,B,C,求一点,到A,B,C的距离和最小
其实这3个例子的本质都是一样的。都是求未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。
以第一个例子为例:
Ax=C 无解
要求||Ax-C||^2最小
A.TAx'=A.TC
x'=(A.TA)^(-1)A.TC
P=Ax'
同理,例子2,3中都需要写成Ax=C 的形式,求最优解。
只是例子2中的最优解是直线y=ax+b中的a,b。例子3中的最优解是P的坐标P(xp,yp)。
使用程序求例子1:A(3,1),C(1,3)
CODE
import numpy as np
from matplotlib import pyplot as plt
A = np.array([[3],[1]])
C = np.array([[1],[3]])
#x'=(A.TA)^(-1)A.TC
B = A.T.dot(C)
AA = np.linalg.inv(A.T.dot(A))#求A.T.dot(A)的逆
l=AA.dot(B)
#P=Ax'
P=A.dot(l)
x=np.linspace(-2,2,10)#x.shape=(10,)
x.shape=(1,10)
#画出直线y=ax
xx=A.dot(x)
fig = plt.figure() #figsize=(10,6)
ax= fig.add_subplot(111)
ax.plot(xx[0,:],xx[1,:])
#画出A点
ax.plot(A[0],A[1],'ko')
#画出C点,P点
ax.plot([C[0],P[0]],[C[1],P[1]],'r-o')
#画出OC线
ax.plot([0,C[0]],[0,C[1]],'m-o')
#画出坐标轴x=0,y=0
ax.axvline(x=0,color='black')
ax.axhline(y=0,color='black')
#标写每个点的字母
margin=0.1
ax.text(A[0]+margin, A[1]+margin, r"A",fontsize=20)
ax.text(C[0]+margin, C[1]+margin, r"C",fontsize=20)
ax.text(P[0]+margin, P[1]+margin, r"P",fontsize=20)
ax.text(0+margin,0+margin,r"O",fontsize=20)
ax.text(0+margin,4+margin, r"y",fontsize=20)
ax.text(4+margin,0+margin, r"x",fontsize=20)
plt.xticks(np.arange(-2,3))
plt.yticks(np.arange(-2,3))
ax.axis('equal')
plt.show()
结果: