吴恩达机器学习课程作业——ML_ex1
第一次用Octave,语法和Matlab一样,熟悉一下即可,主要是对线性回归的整体思路要清晰,对Octave中每个函数一个单独文件的方式理解,跟着“ex1”中的提示就能一步一步的写出核心代码,巩固课程内容。
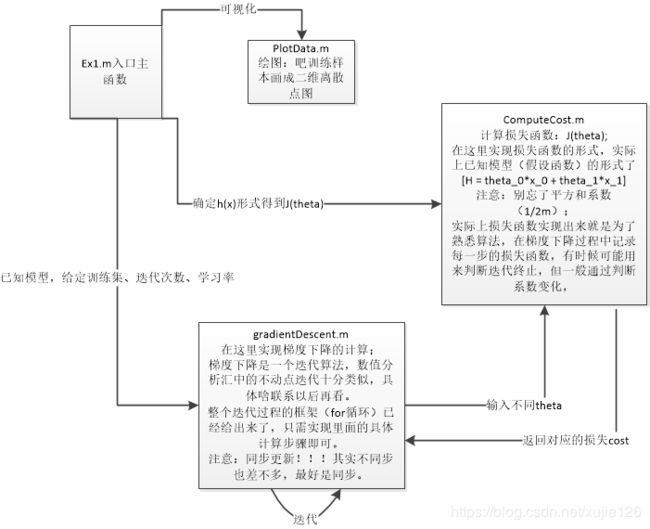
ex1思路清晰,很简单,用来熟悉整个Octave语法和梯度下降的原理:下面记录代码
第一个:需要实现的是ComputeCost.m
function J = computeCost(X, y, theta)
%COMPUTECOST Compute cost for linear regression
% J = COMPUTECOST(X, y, theta) computes the cost of using theta as the
% parameter for linear regression to fit the data points in X and y
% Initialize some useful values
m = length(y); % number of training examples
% You need to return the following variables correctly
J = 0;
% ====================== YOUR CODE HERE ======================
% Instructions: Compute the cost of a particular choice of theta
% You should set J to the cost.
for i= 1:m%遍历每一个训练样本
J += (dot(transpose(theta),X(i,:)) - y(i))^2;%将预测值和真实值得平方相加(即:平方和)
end
J = J/(2*m);%记得除以这个系数
% =========================================================================
end第二个:需要实现的gradientDescent.m
function [theta, J_history] = gradientDescent(X, y, theta, alpha, num_iters)
%GRADIENTDESCENT Performs gradient descent to learn theta
% theta = GRADIENTDESCENT(X, y, theta, alpha, num_iters) updates theta by
% taking num_iters gradient steps with learning rate alpha
% Initialize some useful values
m = length(y); % number of training examples
J_history = zeros(num_iters, 1);
theta_history = theta;
for iter = 1:num_iters
% ====================== YOUR CODE HERE ======================
% Instructions: Perform a single gradient step on the parameter vector
% theta.
%
% Hint: While debugging, it can be useful to print out the values
% of the cost function (computeCost) and gradient here.
%
for n_m = 1:2%对每一个特征循环,这里是(x0,x1)
j = 0;%设置一个临时变量,存储每一个特征(系数)对应的梯度
for i=1:m
j+= (dot(transpose(theta_history),X(i,:))-y(i))*X(i,n_m);%计算梯度(偏导数)
endfor
theta(n_m) = theta_history(n_m) - alpha/m*j; %同步更新哈
endfor
theta_history = theta;%同步更新哈
% ============================================================
% Save the cost J in every iteration
J_history(iter) = computeCost(X, y, theta);
end
end
至此,ex1.m的内容都完成了,可以运行ex1.m查看可视化结果,也可以看输出的结果和正确结果的对比。
下面该ex1_multi.m了:
示例数据是根据房屋面积和卧室数量估计房价;
更上面的数据相比,需要进行归一化处理(特征缩放),在featureNormalize.m文件中对特征进行缩放:
%% ================ Part 1: Feature Normalization ================
function [X_norm, mu, sigma] = featureNormalize(X)
%FEATURENORMALIZE Normalizes the features in X
% FEATURENORMALIZE(X) returns a normalized version of X where
% the mean value of each feature is 0 and the standard deviation
% is 1. This is often a good preprocessing step to do when
% working with learning algorithms.
% You need to set these values correctly
X_norm = X;
mu = zeros(1, size(X, 2));
sigma = zeros(1, size(X, 2));
% ====================== YOUR CODE HERE ======================
% Instructions: First, for each feature dimension, compute the mean
% of the feature and subtract it from the dataset,
% storing the mean value in mu. Next, compute the
% standard deviation of each feature and divide
% each feature by it's standard deviation, storing
% the standard deviation in sigma.
%
% Note that X is a matrix where each column is a
% feature and each row is an example. You need
% to perform the normalization separately for
% each feature.
%
% Hint: You might find the 'mean' and 'std' functions useful.
%
for i = 1:size(X,2)
mu(i) = mean(X(:,i));%样本空间中(训练集)中,求每个特征的样本均值
endfor
for j = 1:size(X,2)
sigma(j) = std(X(:,j));%每个特征的方差
endfor
for k =1:size(X,2)
X_norm(:,k).-= mu(k);%先中心化
X_norm(:,k)./=sigma(k);%再归一化(这里用方差替换了样本空间的范围(max-min))
endfor
% ============================================================
end
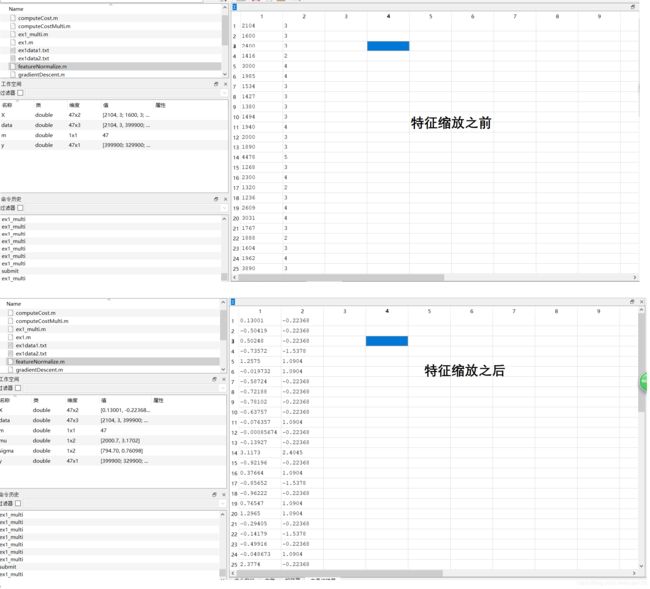
特征缩放之后,训练数据的变化如下所示:
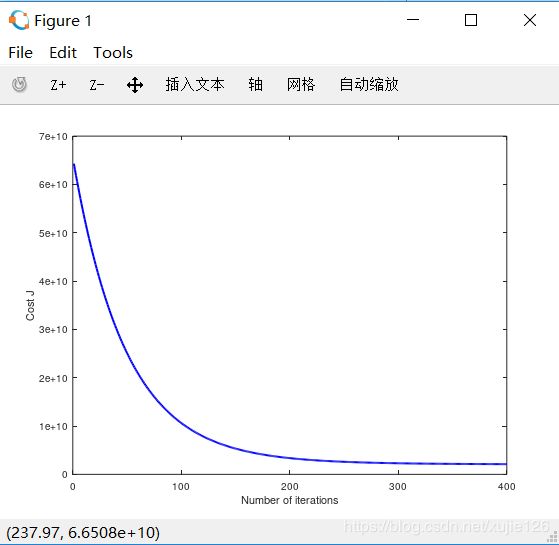
下一步就是梯度下降的实现了
%% ================ Part 2: Gradient Descent ================
实际上,梯度下降代码是可以复用的,只要特征变量数量参数化就可以了,这一点在ex1.m中做的不好:gradientDescentMulti.m
function [theta, J_history] = gradientDescentMulti(X, y, theta, alpha, num_iters)
%GRADIENTDESCENTMULTI Performs gradient descent to learn theta
% theta = GRADIENTDESCENTMULTI(x, y, theta, alpha, num_iters) updates theta by
% taking num_iters gradient steps with learning rate alpha
% Initialize some useful values
m = length(y); % number of training examples
J_history = zeros(num_iters, 1);
n_feature = size(X,2);
temp_theta = theta;%为了保持同步更新
for iter = 1:num_iters
% ====================== YOUR CODE HERE ======================
% Instructions: Perform a single gradient step on the parameter vector
% theta.
%
% Hint: While debugging, it can be useful to print out the values
% of the cost function (computeCostMulti) and gradient here.
%
for n_theta = 1:n_feature
gradient = transpose(X*temp_theta - y)*X(:,n_theta);
theta(n_theta) = temp_theta(n_theta) - alpha*gradient/m;
endfor
temp_theta = theta;
% ============================================================
% Save the cost J in every iteration
J_history(iter) = computeCostMulti(X, y, theta);
end
end
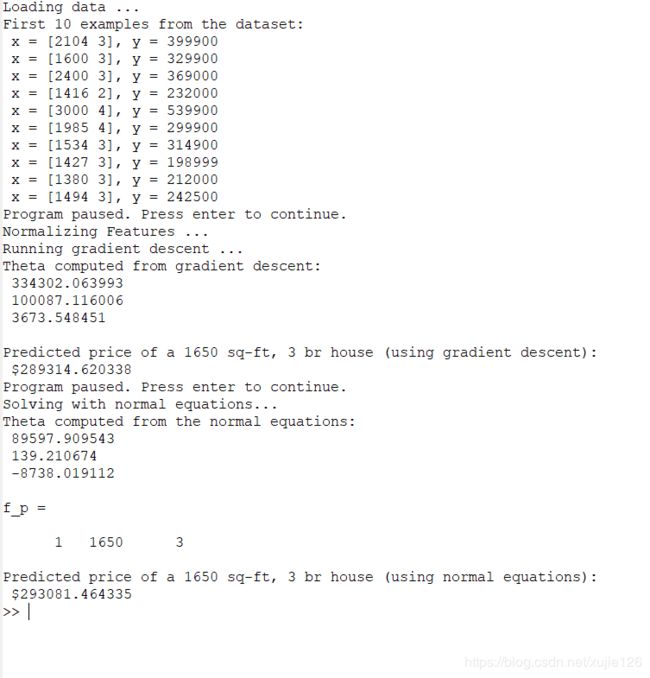
%% ================ Part 3: Normal Equations ================
最后一部分是直接利用正规方程解得直接解,比较简单,但是结果和梯度下降有差别:normalEqn.m
function [theta] = normalEqn(X, y)
%NORMALEQN Computes the closed-form solution to linear regression
% NORMALEQN(X,y) computes the closed-form solution to linear
% regression using the normal equations.
theta = zeros(size(X, 2), 1);
% ====================== YOUR CODE HERE ======================
% Instructions: Complete the code to compute the closed form solution
% to linear regression and put the result in theta.
%
% ---------------------- Sample Solution ----------------------
theta = pinv(transpose(X)*X)*transpose(X)*y;
% -------------------------------------------------------------
% ============================================================
end
END:先告一段落