Python 实现Prim最小生成树算法

最小生成树（MST）：对于带权无向图所有的生成树中，代价最小的生成树称为图的最小生成树。

Prim算法：假设N=(V,E) 是具有n个顶点的连通图，设U是最小生成树中顶点的集合，设TE是最小生成树中边的集合；

                  初始，U = { u1 } ，TE = { } ，

                  重复执行: 在所有 u∈U，v∈V-U 的边 ( u , v ) 中寻找代价最小的边( u’ , v’ ) ，并纳入集合 TE 中；

                                  同时将 v’ 纳入集合 U 中；

                 直至 U = V 为止。

Prim算法也是典型的贪心算法。最小生成树的主要有两个重复过程：寻找一个满足条件的未插入到生成树集合的结点；利用该结点更新其余顶点到生成树集合的最小权值信息。因此，时间复杂度为O()，其中n为图的结点。

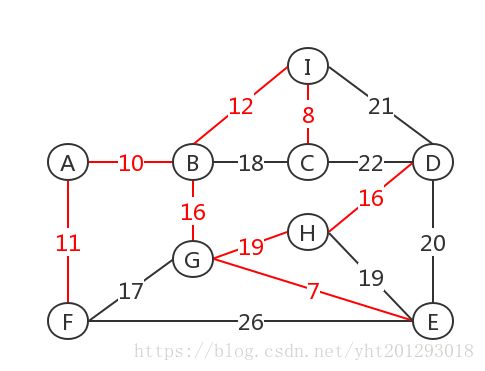
如下图

prim算法过程：初始U={A},V-U={B,C,D,E,F,G,H,I}     TE={}

                                U={A,B},V-U={C,D,E,F,G,H,I}      +(A,B)

                                U={A,B,F},V-U={C,D,E,G,H,I}      +(A,F)

                                U={A.B,F,I},V-U={C,D,E,G,H}      +(B,I) 

                                U={A,B,F,I,C},V-U={D,E,G,H}      +(I,C) 

                                U={A,B,F,I,C,G},V-U={D,E,H}      +(B,G)

                                U={A,B,F,I,C,G,E},V-U={D,H}      +(G,E)

                                U={A,B,F,I,C,G,E,H},V-U={D}      +(G,H)

                                U={A,B,F,I,C,G,E,H,D},V-U={}     +(H,D)

代码实现

 

import sys
if __name__=='__main__':
    MAX = sys.maxsize
    primgraph = [[MAX,  10, MAX, MAX, MAX,  11, MAX, MAX, MAX],
                 [10,  MAX,  18, MAX, MAX, MAX,  16, MAX,  12],
                 [MAX,  18, MAX,  22, MAX, MAX, MAX, MAX,   8],
                 [MAX, MAX,  22, MAX,  20, MAX, MAX,  16,  21],
                 [MAX, MAX, MAX,  20, MAX,  26,   7,  19, MAX],
                 [11,  MAX, MAX, MAX,  26, MAX,  17, MAX, MAX],
                 [MAX,  16, MAX, MAX,   7,  17, MAX,  19, MAX],
                 [MAX, MAX, MAX,  16,  19, MAX,  19, MAX, MAX],
                 [MAX,  12,   8,  21, MAX, MAX, MAX, MAX, MAX]]
    chararray = ['A','B','C','D','E','F','G','H','I']
    charlist = []
    charlist.append(chararray[0])
    mid = []    #mid[i]表示生成树集合中与点i最近的点的编号
    lowcost = []    #lowcost[i]表示生成树集合中与点i最近的点构成的边最小权值 ，-1表示i已经在生成树集合中
    lowcost.append(-1)
    mid.append(0)
    n = len(chararray)
    for i in range(1,n): #初始化mid数组和lowcost数组
        lowcost.append(primgraph[0][i])
        mid.append(0)
    sum = 0
    for _ in range(1,n): #插入n-1个结点
        minid = 0
        min = MAX
        for j in range(1,n):  #寻找每次插入生成树的权值最小的结点
            if(lowcost[j]!=-1 and lowcost[j]primgraph[minid][j]):
                lowcost[j] = primgraph[minid][j]
                mid[j] = minid
    print("sum="+str(sum))
    print("插入结点顺序："+str(charlist))

运行结果

A——B权值：10
A——F权值：11
B——I权值：12
I——C权值：8
B——G权值：16
G——E权值：7
G——H权值：19
H——D权值：16
sum=99
插入结点顺序：['A', 'B', 'F', 'I', 'C', 'G', 'E', 'H', 'D']