机器学习入门——numpy与matplotlib的使用简介
引言
工欲善其事必先利其器，本文就来介绍一下在我们机器学习中会常用到的工具类——Numpy以及matplotlib。
在文章的最后，会用一个实例展示它们是如何一起工作的。
Numpy主要是封装了一些向量、矩阵运算操作，而matplotlib主要用于画图。
文章目录
- 引言
- Numpy
- Numpy基础
- 创建Numpy数组和矩阵
- Numpy.array的基本操作
- 基本属性
- 数据访问
- reshape方法
- Numpy数组和矩阵的合并与分割
- 合并
- 分隔
- Numpy矩阵运算
- Numpy中的聚合运算
- Numpy中的arg运算
- Numpy中的花式索引和批量比较
- matplotlib
- 折线图
- 散点图
- 实例
- 总结
- 参考
Numpy
Numpy中核心的数据结构是array，可以理解为数组。因为它可以方便的操作多维数组，从而可以看成是矩阵。
Numpy基础
加载numpy的方式一般为import numpy as np，如果没有安装的话，先用pip install numpy安装一下。顺便说下，本文使用的语言为python.6.8，本文的代码在Jupyter中运行。
可能有的同学就会问了，python已经有了list这种数据结构，它里面也可以存放list，也可以当做矩阵，为什么还要引入一个numpy呢。
接下来就对比下numpy与list的不同。
对list的操作大家应该很熟悉了：
L = [i for i in range(10)]
print(L[5])
L[5] = 100
print(L)
输出:[0, 1, 2, 3, 4, 100, 6, 7, 8, 9]
Python的list中元素的类型可以不一样的。比如：
L[5] = "Hello"
print(L)#[0, 1, 2, 3, 4, 'Hello', 6, 7, 8, 9]
这样的好处是非常灵活，但是缺点就是效率不高，因为需要检查每个元素的类型。
当然python中还有类型一样的数据结构，比如array。
import array
arr = array.array('i',[i for i in range(10)])# 第一次参数'i'表示整型，说明这是一个整型数组
arr # array('i', [0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
它的操作方式和列表一样。但是它没有将这些数据看成是向量或矩阵，也就没有提供相关的运算。
接下来我们看下今天的注解numpy.array。
nparr = np.array([i for i in range(10)]) # 构造函数中传入序列对象
nparr # array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
它的访问和修改与list一样这里就不展示了，但是值得提醒的是np.array它的类型是固定的。可以通过nparr.dtype#dtype('int32') 来查看它的类型。
构造的时候它可以自动解析传入数据的类型，如果同时传入整型和浮点型它会自动用浮点型保存整个数组：
nparr2 = np.array([1,2,3.0])
nparr2.dtype# dtype('float64')
创建Numpy数组和矩阵
numpy除了可以通过构造函数的方式创建实例对象，还提供了丰富的其他方法。
比如创建零数组/零矩阵。
np.zeros(5)#array([0., 0., 0., 0., 0.])
np.zeros(5).dtype # dtype('float64')
可以看到默认的类型为浮点型。
当然我们也可以指定类型创建整型的零数组：
a = np.zeros(5,dtype=int)
a # array([0, 0, 0, 0, 0])
a.dtype # dtype('int32')
这里我们传入的参数都是一个数，我们也可以传入一个元组：
np.zeros((3,5))
输出:
array([[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.]])
可以看到，这种情况下就是生成了一个3行5类的二维数组(矩阵)。
有了创建零的，当然还有创建一的：
np.ones(10)#array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.])
那如果你想创建一个指定值的矩阵呢，此时可以使用np.full这个方法：
np.full((3,5),7) #指定元素为7
输出:
# 这里默认的类型为整型(如果你传入的是个整数的话)
array([[7, 7, 7, 7, 7],
[7, 7, 7, 7, 7],
[7, 7, 7, 7, 7]])
我们知道python中有range这个方法，对应的np也提供了arange方法：
np.arange(0,20,2) # [0,20) 步长为2，结果为： array([ 0, 2, 4, 6, 8, 10, 12, 14, 16, 18])
看起来和python的range方法类似，不过np.arange返回的是np数组。
不过np.arange接收的步长可以为小数:
np.arange(0,1,0.1) #array([0. , 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9])
步长默认是1。和arange一样，如果省略了起始值，则默认为0：
np.arange(10) #array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
在numpy中还有一个常用的方法，叫linspace，常用于生成x轴坐标。
np.linspace(0,20,10) # 在[0,20]区间等长地分出10个点
输出:
array([ 0. , 2.22222222, 4.44444444, 6.66666667, 8.88888889,
11.11111111, 13.33333333, 15.55555556, 17.77777778, 20. ])
如果想生成[0,20]以2为步长，那么要这么写：
np.linspace(0,20,11) # 在[0,20]区间等长地分出11个点
输出:
array([ 0., 2., 4., 6., 8., 10., 12., 14., 16., 18., 20.])
因为包含起始点和终点共有11个点。
numpy还提供了随机数函数，一起来看一下。
np.random.randint(0,10) # 生成[0,10)之间的随机整数
np.random.randint(0,10,10) # array([4, 0, 1, 3, 3, 0, 7, 1, 8, 8])
第三个参数如果是个数字则代表生成多少个元素的数组。
为了增加可读性，最后一个参数最好指定参数名，如：
np.random.randint(0,10,size =(4,2)) # 从[0,10) 之间生成 4行2列的矩阵
输出:
array([[5, 3],
[0, 4],
[5, 4],
[9, 8]])
如果想每次生成的随机数是一样的，可以指定随机种子。
np.random.seed(666)
np.random.randint(0,10,10)
同时执行这两段代码可以生成的随机数组每次都是一样的，不信的可以试一下。
np.random.random()生成0到1之间的随机小数，可以指定size属性，和randint一样。
还可以生成符合正态分布的随机小数：
np.random.normal()
还可以指定均值和方差: np.random.normal(10,100) # 指定均值为10，方差为100
Numpy.array的基本操作
首先创建一个一维数组：
x = np.arange(10)
x # array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
还可以通过一维数组转换为二维数组:
X = np.arange(15).reshape(3,5)
输出：
array([[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14]])
基本属性
接下来看下它们的基本属性。
查看数组的维度：
x.ndim # 1
X.ndim # 2
查看数组的形状(就是几乘几的数组):
x.shape# (10,)
X.shape# (3, 5)
查看数组元素个数:
x.size # 10
X.size # 15
数据访问
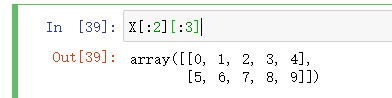
其中和python中访问类似的，如下：
numpy访问的特殊之处有一点是可以传入一个元组：
切片：
接下来我们看下这种写法：
为什么会这样呢，先看下X[:2]:
这是取二维数组中前两行，没问题。
基于这个数组，再取一次[:3]的话，本意是想取前3列。但是python在解析的时候，会解析成取上面那个数组中前3个元素(前3行，二维数组中每个元素都是一行)，但是此时这个数组只有2个元素，因此就全部返回出来了。
如果想取前2行的前3列，我们必须使用,这个运算符X[:2,:3]。
所以使用numpy的时候多维访问也建议使用,。
在numpy中创建子矩阵，对子矩阵进行修改也会影响原矩阵。
numpy优先考虑的是效率，采用类似引用的方式，原矩阵和子矩阵的修改会互相影响。
如果想拷贝份新的可以使用copy函数：
reshape方法
注意10x1的数组和1x10的数组是完全不同的。
我们在reshape的时候还可以只指定一个维度的数据，另一个让机器帮我们计算：
Numpy数组和矩阵的合并与分割
合并
在np.concatenate参数中的列表元素个数是不限的。
对于矩阵也是一样的：
上面介绍的是沿着行的方向拼接，可以通过axis=1参数指定沿着列的方向(按列拼接)拼接：
那如果想拼接数组和矩阵要怎么做呢：
可能有的同学会觉得这样写太麻烦了，那么还有一个方法是适合你的：
那么肯定有横向叠加：
分隔
注意边界点。
对于矩阵的分割也是一样的：
可以看到以上分割默认是基于行(axis=0)进行分割的。那基于列的分割是怎样的：
如果觉得以上的写法不够直观，numpy还提供了更加直观的方法：
那数据分隔有什么意义呢
假设我们加载进来的样本数据如上，最后一列是每行样本所属的标签。
我们就可以把特征和标签进行分开(其实pandas更加适合处理这种问题，以后会介绍)
Numpy矩阵运算
给定一个向量，需要将向量中每个元素的乘以2：
那么这种写法的效率如何呢?
可能看到0.1s左右觉得还行，但是numpy会让你知道什么才叫效率。
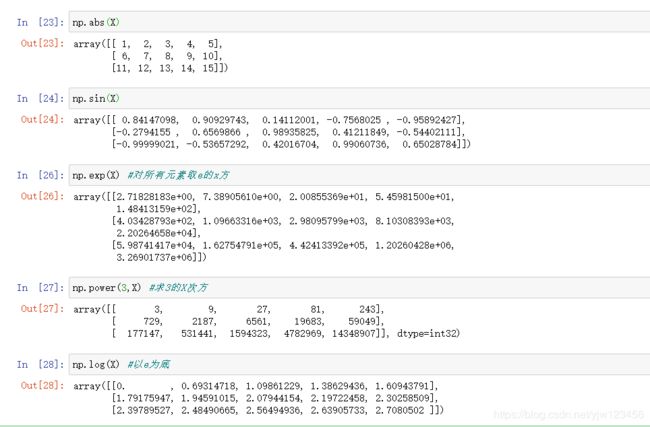
这就是numpy，它直接把数组当做向量，把二维数组当做矩阵，支持很多向量和矩阵的运算。
同样还支持幂运算。
对于求绝对值，求sin等都可以应用于矩阵上的每个元素。
numpy还支持矩阵之间的运算。
还有一个常用的运算是求矩阵的转置。
接下来看下向量和矩阵的运算。
上面是向量和矩阵的加法，如果做乘法会怎样呢
矩阵还有一个非常重要的运算叫矩阵的逆
注意，只有方阵才存在逆矩阵。
Numpy中的聚合运算
就是把一组值变成一个值，比如求均值、求和等。
接下来看下numpy的效果与python的对比
上面都是向量的聚合运算，接下来看下二维矩阵:
numpy还提供了其他的聚合函数：
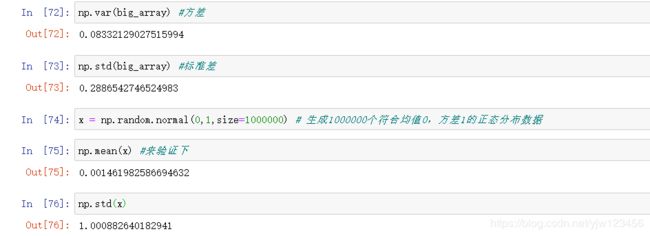
numpy还提供了了方差和均值等方法：
Numpy中的arg运算
有时我们想知道最小的值在哪(索引)，而不仅仅知道它的值。
接下来介绍如何排序。
同样地，对矩阵也可以进行排序。
那排序中如何使用索引呢
当然，arg还能对矩阵使用。
Numpy中的花式索引和批量比较
花式索引是什么？
上面的就是花式索引，花式索引还可以是二维数组。
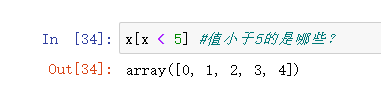
花式索引还支持bool值索引:
bool值索引是非常有用的，经常用在批量比较中：
numpy支持复杂的比较，同时二维数组也支持比较：
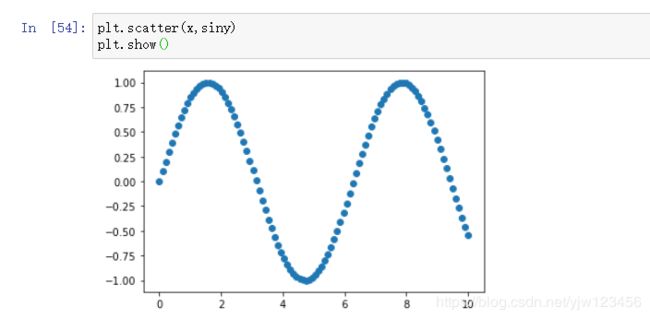
得到这些bool数组后除了可以进行筛选，还可以进行一些聚合运算：
当然对二维数组是同样有效的：
对于这些比较是可以组合的：
重点是要会用这种写法：
numpy的操作基本上介绍完了，下面介绍下另一个常用的工具——画图。
matplotlib
折线图
废话不多说，直接上代码：
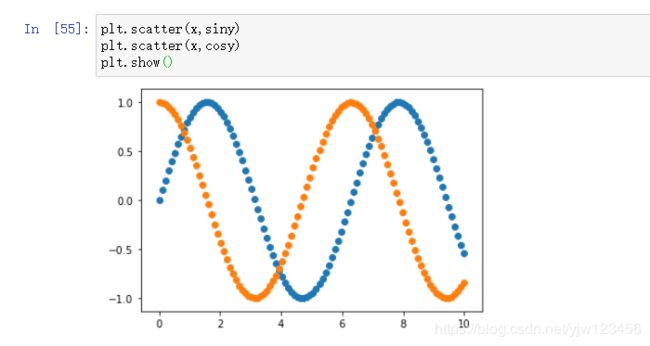
接下来来画一个sin函数图像
它的实质是x有100个点,y也有100个点，让后用线把这些点连接起来，看上去就成了曲线。
在一个图像中可以绘制多条曲线。
当然我们可以手动指定颜色：
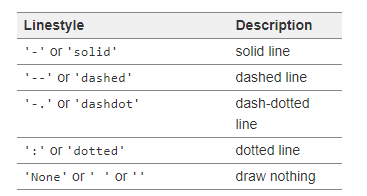
我们还可以修改绘制线条的样式：
其中linestyle的可选值如下：
如果我们仔细观察绘制的图像，可以发现，自动为我们调整好了坐标的间隔，以及y轴坐标的上下限和间隔。
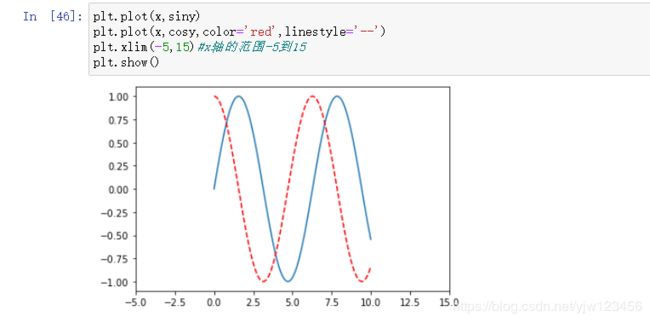
当然我们可以手动调整：
因为在[-5,0]和[10,15]这些点之间没有对应的y值，因此看起来就没有任何点在上面。
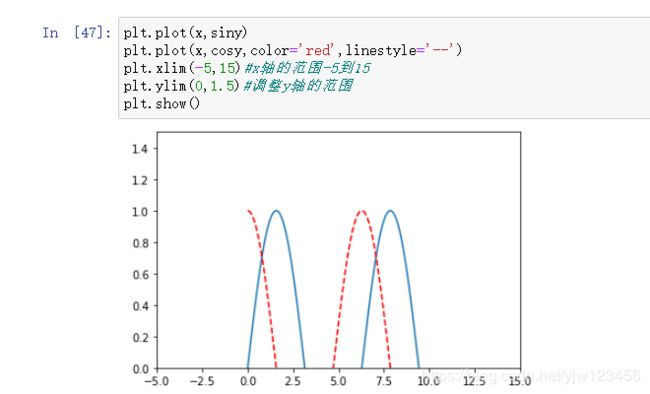
还有个方法可以同时调整这两个轴的范围
有时需要告诉别人x,y轴分别代表什么：
还可以给这些曲线增加图示：
我们还可以为整幅图增加标题：
上面介绍的都是折线图，还有一种常见的是散点图，接下来看下如何绘制。
散点图
散点图(scatter plot)
很简单，比plot替换为scatter即可。可以看到，每个点更加明显，并且点与点之间没有线相连。
要注意的是，折线图通常x轴代表特征,y轴代表标签；而散点图x和y都表示特征。通常散点图用于表示分布。
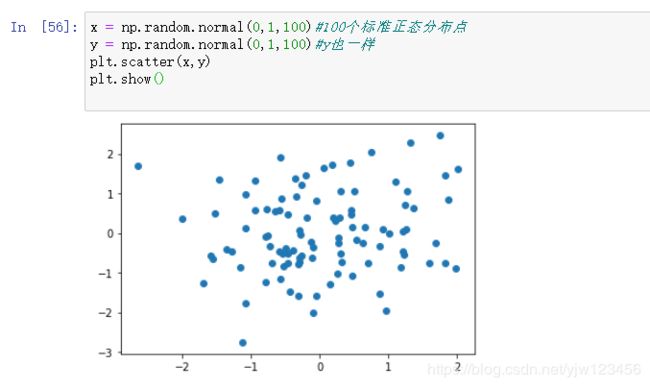
我们绘制下高斯分布的图像：
可能100个点看不出它的均值和方差，我们改成1000试下：
这就是一个标准的二维正态分布。
这里有个参数可以控制透明度：
实例
接下来我们介绍下如何从sklearn中加载数据并绘制出来。
我们从sklearn#datasets模块中加载数据，它提供了各种各样的数据。
我们以鸢尾花数据集为例
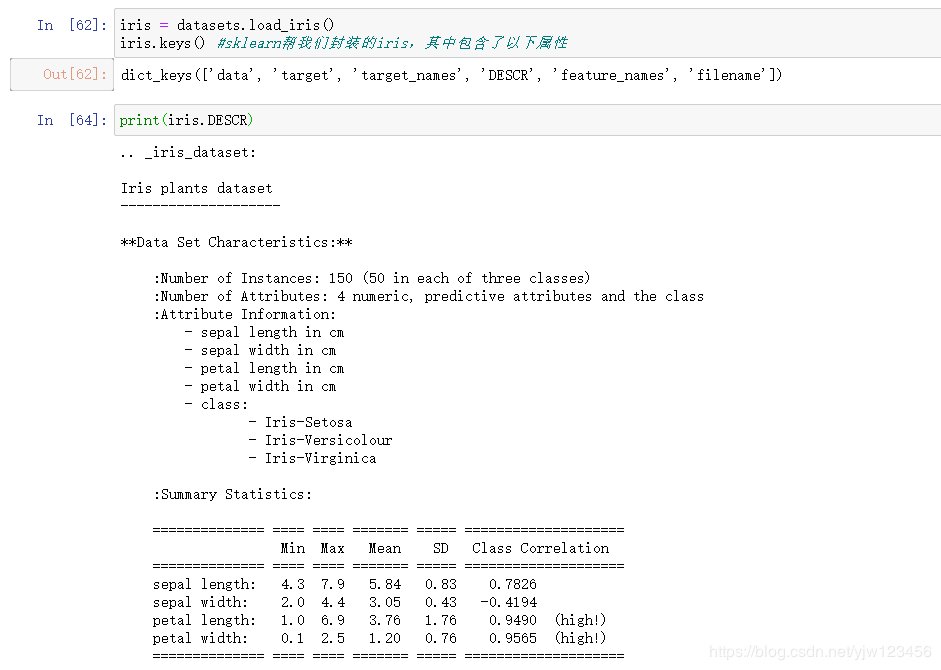
可以通过DESCR来看一下这个数据集的介绍。接下来通过data来看下它的数据长什么样的。
它其实就是一个numpy的矩阵，有4列，分别对应4个特征:sepal length,sepal width,petal length,petal width。
我们接下来通过可视化这些数据，一般是绘制二维图像，所以我们只去前两个特征:
但是这个图的信息量不够，我们只看到了每个点对应的萼片长度是x轴,萼片宽度是y轴。
我们可能需要用不同的颜色标出属于不同类别的花。
y = iris.target
plt.scatter(X[y==0,0],X[y==0,1],color='red')#绘制第一个类别对应的散点图 ，y==0对应的两个特征
plt.scatter(X[y==1,0],X[y==1,1],color='blue')
plt.scatter(X[y==2,0],X[y==2,1],color='green')
plt.show()
这里用到了numpy花式索引中的bool索引。
在散点图中，我们可以设置点的样式：
y = iris.target
plt.scatter(X[y==0,0],X[y==0,1],color='red',marker='o')#绘制第一个类别对应的散点图 ，y==0对应的两个特征
plt.scatter(X[y==1,0],X[y==1,1],color='blue',marker='+')
plt.scatter(X[y==2,0],X[y==2,1],color='green',marker='x')
plt.show()
具体支持哪些样式可以查阅文档。
从绘制的结果可以看出，第1类和第2，第3类非常好区分，是线性可分的。
而第2类和第3类是很难区分的，线性不可分。
但是这里我们只用了前两个维度，如果用后两个维度是怎样的呢？
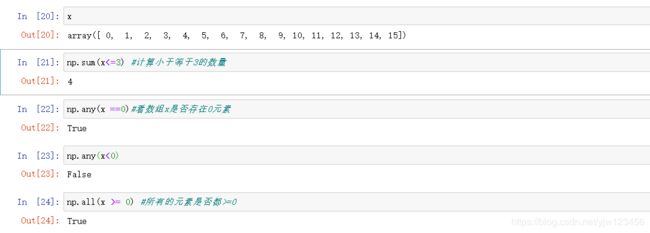
X = iris.data[:,2:]#取所有的行，但是只取后两列
y = iris.target
plt.scatter(X[y==0,0],X[y==0,1],color='red',marker='o')#绘制第一个类别对应的散点图 ，y==0对应的两个特征
plt.scatter(X[y==1,0],X[y==1,1],color='blue',marker='+')
plt.scatter(X[y==2,0],X[y==2,1],color='green',marker='x')
plt.show()
可以看到，红色的点还是和其他颜色的点更容易区分开来。
这就是我们用可视化技术可以得到的信息，可以帮助我们选取合适的机器学习方法。
总结
我们本篇主要学习了numpy的基础知识，然后了解了下如何可视化数据，最后用一个实例进行了说明。接下来开始学习第一个机器学习方法——K临近
参考
1.Python3入门机器学习
- 上一篇：机器学习入门——机器学习基础概念
- 下一篇：机器学习入门——K近邻算法