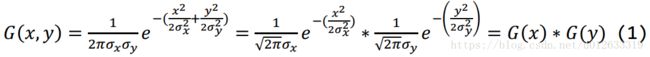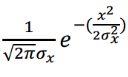OpenCV源码之高斯模糊GaussianBlur, getGaussianKernel

目录

getGaussianKernel

基本原理：

基本流程：

高斯模板创建过程

Step1：构建高斯矩阵

Step2：计算高斯矩阵的和

Step3：归一化

返回值

源码

结论：

参考文章：

---

getGaussianKernel

基本原理：

在数字图像处理中，一般取二维高斯函数为

由（1）可以知道，二维高斯函数，可以看成两个一维高斯函数乘积，因此先计算一维高斯模板，再计算需要的二维高斯模板。

基本流程：

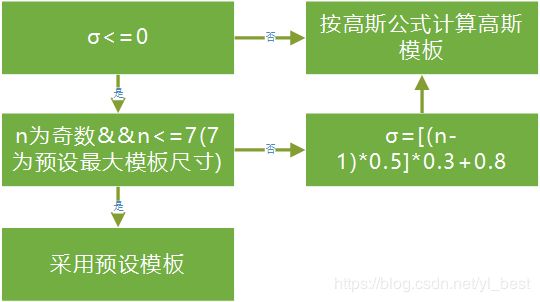
• 取固定系数

当kernels的尺寸为1,3,5,7 并且用户没有设置sigma的时候(sigma <= 0),就会取固定的系数.这是一种默认的值是高斯函数的近似.

• 按照高斯公式计算

当kernels尺寸超过7的时候,如果sigma设置合法(用户设置了sigma),则按照高斯公式计算.当sigma不合法(用户没有设置sigma),则按照sigma=((n-1)0.5 - 1)0.3 + 0.8计算.n为kernels的尺寸.

高斯模板创建过程

Step1：构建高斯矩阵

注意：后续归一化时系数会被去掉，所以会省略系数的计算，只计算​​​​

OpenCV中源码：

double x = i - (n-1)*0.5;
double t = fixed_kernel ? (double)fixed_kernel[i] : std::exp(scale2X*x*x);

笔者修改后：可以参考下图

double sigmaX = sigma > 0 ? sigma : ((n - 1)*0.5 - 1)*0.3 + 0.8;
double scale2X = -0.5 / (sigmaX*sigmaX);
int center = (n - 1) *0.5;
for (int i = 0; i < n; i++)
{
   double x = i - center;
   double t = std::exp(scale2X*x*x);
}

举例：n=7, sigma = 1,中心点center = (7-1)/2=3

Step2：计算高斯矩阵的和

Step3：归一化

矩阵中每一项/矩阵和

返回值

n行*1列的垂直方向的高斯核。水平方向的高斯核只需要对垂直方向高斯核进行转置即可。

源码

cv::Mat cv::getGaussianKernel( int n, double sigma, int ktype )
{
    const int SMALL_GAUSSIAN_SIZE = 7;
    //定义了固定的filter即Kernels.
    static const float small_gaussian_tab[][SMALL_GAUSSIAN_SIZE] =
    {
        {1.f},
        {0.25f, 0.5f, 0.25f},
        {0.0625f, 0.25f, 0.375f, 0.25f, 0.0625f},
        {0.03125f, 0.109375f, 0.21875f, 0.28125f, 0.21875f, 0.109375f, 0.03125f}
    };
//对滤波器的类型进行判断,1,尺寸为奇数;2,尺寸小于等于7;3.sigma小于等于0(注)
    const float* fixed_kernel = n % 2 == 1 && n <= SMALL_GAUSSIAN_SIZE && sigma <= 0 ?
        small_gaussian_tab[n>>1] : 0;
//前文注释中介绍了,Kernels的数据类型为float,double也是ok的.
    CV_Assert( ktype == CV_32F || ktype == CV_64F );
    Mat kernel(n, 1, ktype);
    float* cf = kernel.ptr();
    double* cd = kernel.ptr();
//确定sigma,如果sigma > 0,ok,不用修改;否则按照公式计算(注)
    double sigmaX = sigma > 0 ? sigma : ((n-1)*0.5 - 1)*0.3 + 0.8;
    double scale2X = -0.5/(sigmaX*sigmaX);//高斯公式
    double sum = 0;

    int i;
    for( i = 0; i < n; i++ )
    {
        double x = i - (n-1)*0.5;
        //如果fixed_kernel为真,也就是符合上文中的3个条件,则区固定的系数;否则按照高斯公式计算
        double t = fixed_kernel ? (double)fixed_kernel[i] : std::exp(scale2X*x*x);
        //对kernels进行归一化
        if( ktype == CV_32F )
        {
            cf[i] = (float)t;
            sum += cf[i];
        }
        else
        {
            cd[i] = t;
            sum += cd[i];
        }
    }

    sum = 1./sum;
    for( i = 0; i < n; i++ )
    {
        if( ktype == CV_32F )
            cf[i] = (float)(cf[i]*sum);
        else
            cd[i] *= sum;
    }
    return kernel;
}

结论：

1. OpenCV的GaussianBlur本质上依然是filter2D,

只是针对一些特殊情况进行了GPU和CPU版本的优化,

如果输入的维度等信息不满足这些特殊情况,则选择使用filter2D进行计算

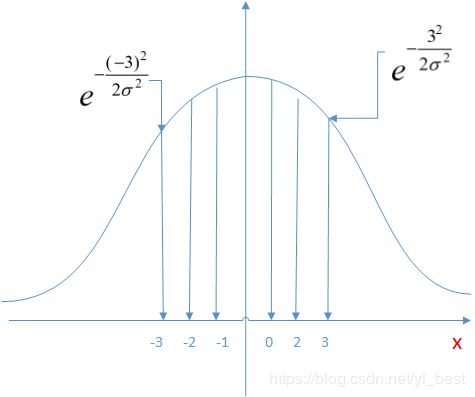
2. 根据高斯函数的分布特性,可以知道,函数分布在区间[u - 3 * sigma, u + 3 * sigma]范围内的概率大于99%.

因此模板大小的选取往往与sigma有关.

createGaussianKernels()代码中的公式,ksize = round(2 * 3 * sigma + 1) | 1; 注意与1按位或,是保证结果为奇数.

另外需要注意,OpenCV认为当图像类型为CV_8U的时候能量集中区域为3 * sigma,

其他类型图像的能量集中区域为4*sigma.

参考文章：

《手撕OpenCV源码之高斯模糊》

https://cloud.tencent.com/developer/article/1165877

 

《OpenCV2.4.13源码分析-getGaussianKernel》

https://blog.csdn.net/u012633319/article/details/80921023