机器学习求索之路（2）--- 逻辑回归

机器学习求索之路（2）— 逻辑回归

@(Machine Learning)

---

1. 原理

  线性回归的模型是求出输出特征向量$Y$和输入样本矩阵$X$之间的线性关系系数$\theta$，满足$\mathbf{Y}={\theta }^{\mathbf{T}}\mathbf{X}$。此时$Y$是连续的，所以是回归模型。如果$Y$是离散的话，就需要对这个$Y$再做一次函数转换，变为$g(Y)$。如果令$g(Y)$的值在某个实数区间的时候是类别A，在另一个实数区间的时候是类别B，以此类推，就得到了一个分类模型。如果结果的类别只有两种，那么就是一个二元分类模型了。逻辑回归的出发点就是从这来的。
  假设有一个二分类问题，输出为$y\in \{0,1\}$，而线性回归模型产生的预测值为$z=w^{T}x+b$是实数值，希望找到一个理想的阶跃函数来帮我们实现$z$值到0/1值的转化。
$$\Theta \left(z\right)=\{\begin{array}{cc}0& ifz<0\\ 0.5& ifz=0\\ 1& ifz>0\end{array}$$

  然而该函数不连续，我们希望有一个单调可微的函数在函数$g$上的转换，于是找到了Sigmoid函数来替代。
$$g(z)=\frac{1}{1+e^{-z}}$$
两者的图像如下图所示:

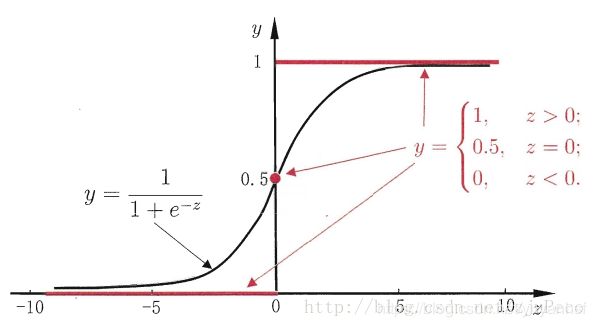
  它有一个非常好的性质，即当$z$趋于正无穷时，$g(z)$趋于1，而当$z$趋于负无穷时，$g(z)$趋于0，这非常适合于我们的分类概率模型。另外，它还有一个很好的导数性质：$g^{{}^{\prime }}(z)=g(z)(1-g(z))$
令$g(z)$中的$z$为：$z={\theta }^{T}x$，这样就得到了二元逻辑回归模型的一般形式：
$$h_{\theta }(x)=g({\theta }^{T}x)=\frac{1}{1+e^{-{\theta }^{T}x}}$$

其中x为样本输入，$h_{\theta }(x)$为模型输出，可以看作是被分到某个类别的概率大小。而$\theta$为分类模型的要求出的模型参数。于是，我们把Sigmoid函数计算得到的值大于等于0.5的归为类别1，小于0.5的归为类别0。($y=0.5$是临界情况，此时$x\theta =0$为， 从逻辑回归模型本身无法确定分类，一般默认为正类)
$$\hat{y}=\{\begin{array}{cc}1& ifh(x)\ge 0.5\\ 0& otherwise\end{array}$$

2. 损失函数

2.1. 损失函数推导

  由于线性回归是连续的，所以可以使用模型误差的的平方和来定义损失函数。而逻辑回归不是连续的，使用误差的的平方和作为损失函数就不合适了，需要使用用最大似然法来推导出逻辑回归的损失函数。
  假设样本输出有0或者1两类，那么
    $P(y=1|x,\theta )=h_{\theta }(x)$
    $P(y=0|x,\theta )=1-h_{\theta }(x)$
可以通过一定的特性将两式合到一起，即：
$$P(y|x,\theta )=h_{\theta }(x{)}^y(1-h_{\theta }(x){)}^{1-y}$$
其中y的取值为0或者1。

  为了求解模型系数$\theta$及求解方便，我们使用对数似然函数最大化，对数似然函数取反即为逻辑回归的损失函数$J(\theta )$。似然函数的代数表达式为：
$$L(\theta )=\prod _{i=1}^m(h_{\theta }(x^{(i)}){)}^{y^{(i)}}(1-h_{\theta }(x^{(i)}){)}^{1-y^{(i)}}$$
其中$m$为样本的个数。
对似然函数对数化取反的表达式，即损失函数$J(\theta )$表达式为：
$$J(\theta )=-lnL(\theta )=-\sum _{i=1}^m(y^{(i)}log(h_{\theta }(x^{(i)}))+(1-y^{(i)})log(1-h_{\theta }(x^{(i)})))$$

2.2. 损失函数求解

  这里使用梯度下降法推导出$\theta$每次迭代的公式，梯度的负方向就是代价函数下降最快的方向。借助于泰特展开有：$f(x+\theta )-f(x)\approx f^{\prime }(x)\cdot \theta$，其中，$f\prime (x)$和$\theta$为向量，那么这两者的内积就等于:
$$f^{\prime }(x)\cdot \theta =||f^{\prime }(x)||\cdot ||\theta ||\cdot cos\delta$$
当$\delta =\pi$时，也就是$\theta$在$f\prime (x)$的负方向上时，取得最小值，也就是下降的最快的方向。
所以有：$${\theta }_j:={\theta }_j-\alpha \frac{\partial J(\theta )}{\partial \theta }$$
其中，${\theta }_j$表示第$j$个特征的权重；$\alpha$为学习率，用来控制步长。

$$\begin{array}{rl}\frac{\partial J(\theta )}{\partial {\theta }_j}& =-\frac{1}{m}\sum _{i=1}^m(y^{(i)}\frac{1}{h(x^{(i)})}-(1-y^{(i)})\frac{1}{1-h(x^{(i)})})\frac{\partial h(x^{(i)})}{\partial {\theta }_j}\\ & =-\frac{1}{m}\sum _{i=1}^m(y^{(i)}\frac{1}{g({\theta }^T{x}^{(i)})}-(1-y^{(i)})\frac{1}{1-g({\theta }^T{x}^{(i)})})g({\theta }^T{x}^{(i)})(1-g({\theta }^T{x}^{(i)}))\frac{\partial {\theta }^T{x}^{(i)}}{\partial {\theta }_j}\\ & =-\frac{1}{m}\sum _{i=1}^m(y^{(i)}(1-g({\theta }^T{x}^{(i)}))-(1-y^{(i)})g({\theta }^T{x}^{(i)}))x_j^{(i)}\\ & =-\frac{1}{m}\sum _{i=1}^m(y^{(i)}-g({\theta }^T{x}^{(i)}))x_j^{(i)}\end{array}$$

$\theta$更新过程可以写成：
$${\theta }_j:={\theta }_j-\alpha \frac{1}{m}\sum _{i=1}^m(h(x^{(i)})-y^{(i)})x_j^{(i)}$$

3. 正则化和模型评估

3.1. 正则化

  逻辑回归也会面临过拟合问题，常见的有L1正则化和L2正则化，和上篇线性回归类似。
  逻辑回归的L1正则化的损失函数表达式如下，相比普通的逻辑回归损失函数，增加了L1的范数做作为惩罚，超参数$\alpha$作为惩罚系数，调节惩罚项的大小。

$$J(\theta )=-\frac{1}{m}\sum _{i=1}^m(y^{(i)}log(h_{\theta }(x^{(i)}))+(1-y^{(i)})log(1-h_{\theta }(x^{(i)})))+||\theta |{|}_1$$
其中 $||\theta |{|}_1$为 $\theta$的L1范数。
  逻辑回归的L2正则化损失函数表达式如下：
$$J(\theta )=-\frac{1}{m}\sum _{i=1}^m(y^{(i)}log(h_{\theta }(x^{(i)}))+(1-y^{(i)})log(1-h_{\theta }(x^{(i)})))+\frac{1}{2}\alpha ||\theta |{|}_2^2$$
其中 $||\theta |{|}_2$为 $\theta$的L2范数。

3.2. 模型评估

  AUC是一个模型评价指标，用于二分类模型的评价。AUC是“Area under Curve（曲线下的面积）”的英文缩写，而这条“Curve（曲线）”就是ROC曲线。
  ROC曲线的横坐标是伪阳性率（也叫假正类率，False Positive Rate），纵坐标是真阳性率（真正类率，True Positive Rate），相应的还有真阴性率（真负类率，True Negative Rate）和伪阴性率（假负类率，False Negative Rate）。这四类的计算方法如下：

• 伪阳性率（FPR）
  判定为正例却不是真正例的概率
• 真阳性率（TPR）
  判定为正例也是真正例的概率
• 伪阴性率（FNR）
  判定为负例却不是真负例的概率
• 真阴性率（TNR）
  判定为负例也是真负例的概率

  当测试集中的正负样本的分布变化的时候，ROC曲线能够保持不变。根据每个测试样本属于正样本的概率值从大到小排序，依次将 “Score”值作为阈值threshold，当测试样本属于正样本的概率大于或等于这个threshold时，认为它为正样本，否则为负样本。
一个典型的ROC曲线如下图：

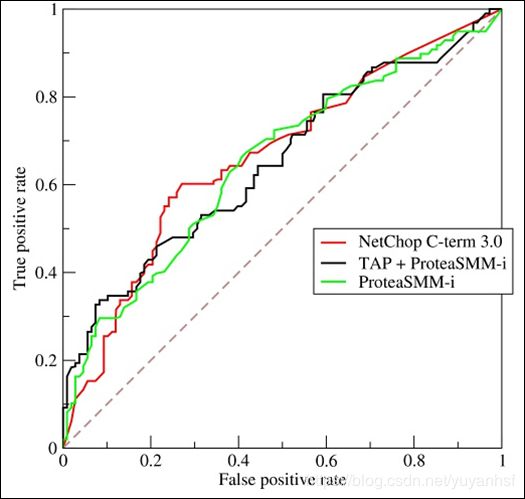
计算出ROC曲线下面的面积，就是AUC的值。 介于0.5和1.0之间，越大越好。

4. 类别不平衡问题

  如果我们的训练集有1000条数据，其中正例2，负例998。那么学习方法只需要返回一个永远将新样本预测为反例的学习器，就能达到99.8%的精度。但是这样的学习算法没有价值，因为它不能预测出任何正例。
  类别不平衡问题是指分类任务中不同类别的训练例数相差很大的情况。在实际工作中，我们经常遇到类别不平衡，例如通过拆分法解决多分类问题时，即原始问题中不同类别的训练样例数目相当，在使用OvR，MvM策略后，二分类任务仍然可能类别不平衡。

处理这个问题一般有3个方法：

• 欠采样。直接对训练集里反例（当前假定反例数目远大于正例）删除一部分，直到正例和反例的数目相当。但是这样可能会丢失一些重要信息。欠采样的代表性算法是利用集成学习机制，将反例划分为若干个集合供不同的学习器使用。这样对每个学习器都进行了欠采样，但在全局来看却不会丢掉重要信息。
• 过采样。对训练集里的正例进行过采样。增加一些正例使得正反例数目接近。但是不能直接对正例进行复制。这样容易引起过拟合。一般的采用代表性算法SMOTE算法。它是通过对训练集里的正例进行插值来产生额外的正例。
• 再缩放。基于原始训练集进行学习
    令$y$表示正例的可能性，$\frac{y}{1-y}$则反映了正例和反例可能性的比值。阈值设为0.5表明分类器认为正例，负例的可能性相同。即分类器规则为: $\frac{y}{1-y}则预测为正例$
    然而，当训练集中正例和负例的数目不同时，令$m^{+}$表示正例的数目，$m^{-}$表示负例数目，则观察几率是$\frac{m^{+}}{m^{-}}$,由于我们通常假设训练集是真实样本总体的无偏差采样，因此观察几率代表了真实几率。于是，只要分类器的预测几率高于观察几率就应判定为正例。即
  $$\frac{y}{1-y}>\frac{m^{+}}{m^{-}}则预测为正例$$
    但是我们的分类器是基于第一个式子进行决策，因此，需对其预测值进行调整，使其执行第一个式子的时候，实际上是在执行第二个式子。那么只需令
  $$\frac{y^{\prime }}{1-y^{\prime }}=\frac{y}{1-y}\ast \frac{m^{-}}{m^{+}}$$

5. 优缺点

• 优点：计算代价不高，易于理解和实现（模型的可解释性在实际工作中极其重要！！！）。
• 缺点：
• 容易产生欠拟合。
• 分类精度不高。

  logistic回归一般应用于二分类领域，可以得出概率值，适用于根据分类概率排名的领域，如搜索排名等。Logistic回归的扩展softmax可以应用于多分类领域，如手写字识别等。

6. Python调用及参数

from sklearn import datasets
import numpy as np
from sklearn.cross_validation import train_test_split
from sklearn.linear_model import LogisticRegression

iris = datasets.load_iris()
X = iris.data[:, [2, 3]]
y = iris.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)

lr = LogisticRegression(C=100, random_state=0)
lr.fit(X_train, y_train)
lr.predict_proba(X_test) # 查看测试样本属于各个类别的概率

参数解释

• C：C为正则化系数λ的倒数，通常默认为1。设置越小则对应越强的正则化。
• dual : 对偶或者原始方法。Dual只适用于正则化相为l2 liblinear的情况，通常样本数大于特征数的情况下，默认为False
• penalty: 正则化项。penalty参数可选择的值为"l1"和"l2"。分别对应L1的正则化和L2的正则化，默认是L2的正则化。
• solver: solver参数决定了我们对逻辑回归损失函数的优化方法，有4种算法可以选择：
  • liblinear：使用了开源的liblinear库实现，内部使用了坐标轴下降法来迭代优化损失函数。
  • lbfgs：拟牛顿法的一种，利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。
  • newton-cg：也是牛顿法家族的一种，利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。
  • sag：即随机平均梯度下降，是梯度下降法的变种，和普通梯度下降法的区别是每次迭代仅仅用一部分的样本来计算梯度，适合于样本数据多的时候。
    注：newton-cg, lbfgs和sag这三种优化算法时都需要损失函数的一阶或者二阶连续导数，因此不能用于没有连续导数的L1正则化，只能用于L2正则化。而liblinear可使用L1正则化和L2正则化
• multi_class: 决定了多分类方式的选择，有 ovr和multinomial两个值可以选择，默认是 ovr。
• class_weight：用于标示分类模型中各种类型的权重，可以不输入，即不考虑权重，或者说所有类型的权重一样。两种情况下可使用这个参数：误分类的代价很高和样本高度失衡