基于Qt的OpenGL编程（3.x以上GLSL可编程管线版）---(二十五)几何着色器

Vries的教程是我看过的最好的可编程管线OpenGL教程，没有之一，其原地址如下，https://learnopengl-cn.github.io/04%20Advanced%20OpenGL/09%20Geometry%20Shader/ 关于几何着色器的详细知识了解请看原教程，本篇旨在对Vires基于visual studio平台的编程思想与c++代码做纯Qt平台的移植，代码移植顺序基本按照原教程顺序，并附加一些学习心得，重在记录自身学习之用

Tip1：Qt的QOpenGLShader这个类可以直接指定Geometry类型着色器，指定完后用QOpenGLShaderProgram类，链接即可。

Tip2: 这节的代码基本与着色器本身有关，所以着色器部分的直接复制Vries的代码即可。

Tip3: 几何着色器在处理简单且重复的形状特别有用！！ 比如“我的世界”中的立方体格子。

Tip4: 安利一个免费的在线绘图工具，比Edraw方便，浏览器就能打开使用：https://www.draw.io/

 

程序源代码链接：https://pan.baidu.com/s/1zURVmd9KpY0ZV6KCEK8-MA  提取码：xlgr 

编译环境：Qt5.9.4

编译器：Desktop Qt5.9.4 MSVC2017 64bit

IDE：QtCreator

 

一. 如何在Qt里使用几何着色器

1.1 简介

  几何着色器（Geometry Shader）是个啥子呦，我对他的理解是点的扩张与修改器，可以在顶点着色器（Vertex Shader）将数据传往片段着色器（Fragment Shader）的过程中，拦截数据加以修改，再传往片段着色器。

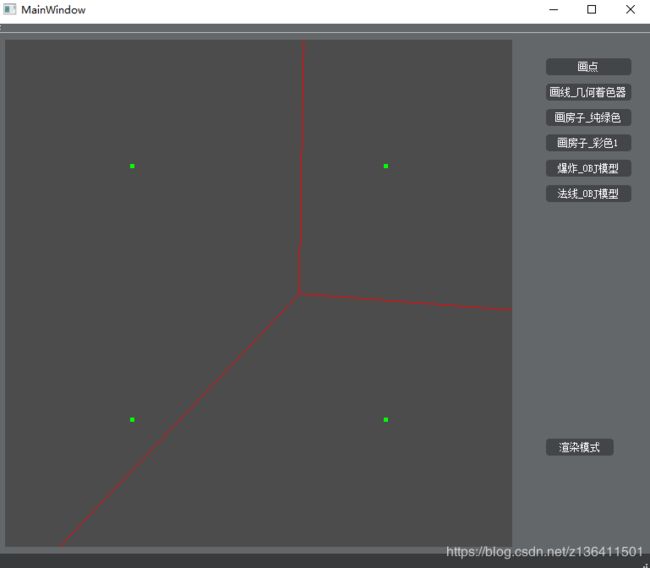
举一个简单的例子，往顶点着色器传进四个点，如下：

float points[] = {
    -0.5f,  0.5f, // 左上
     0.5f,  0.5f, // 右上
     0.5f, -0.5f, // 右下
    -0.5f, -0.5f  // 左下
};

通过几何着色器将每一个点扩张成两个点，并连成一条直线，如下图：

1.2 使用几何着色器

  QOpenGLShader里包含了Geometry的设置属性，所以直接设置即可。设置完后，将其与顶点着色器，片段着色器一同添加进QOpenGLShaderProgram管理器进行管理。

  添加步骤如图下所示：

QOpenGLShader geometryShader(QOpenGLShader::Geometry);
bool success  = geometryShader.compileSourceFile(geometrySource); //geomertySource是几何着色器文件所在的路径
if(!success){
  qDebug() << "ERROR::SHADER::GEOMETRY::COMPILATION_FAILED" << endl;
  qDebug() << geometryShader.log() << endl; //如果几何着色器生成错误，.log()函数会返回出错信息
}

shaderProgram = new QOpenGLShaderProgram();
shaderProgram->addShader(&geometryShader); //将几何着色器添进总着色器中。
shaderProgram->addShader(&vertexShader);
shaderProgram->addShader(&fragmentShader);

1.3 用几何着色器画房子

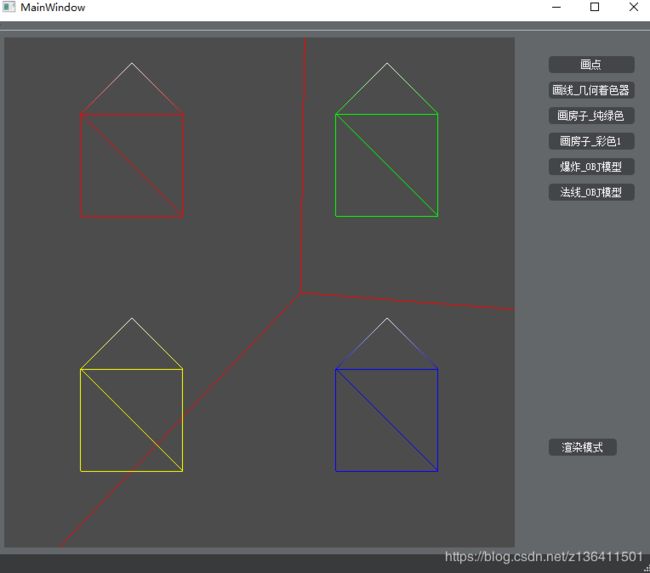
如何使用几何着色器将四个简单的point转换为房子呢？

拿着色器代码解释：

下述为传进的数据，每行前两个元素为点的二维坐标，后三个为该点的rgb颜色值。

float points[] = {
    -0.5f,  0.5f, 1.0f, 0.0f, 0.0f, // 左上
     0.5f,  0.5f, 0.0f, 1.0f, 0.0f, // 右上
     0.5f, -0.5f, 0.0f, 0.0f, 1.0f, // 右下
    -0.5f, -0.5f, 1.0f, 1.0f, 0.0f  // 左下
};

colhouse.vert

//没什么解释的，很简单的着色器
#version 330 core
layout (location = 0) in vec2 aPos;
layout (location = 1) in vec3 aColor;

out VS_OUT{
  vec3 color;
} vs_out;

void main(){
  vs_out.color = aColor;  //把颜色传往下一个着色器
  gl_Position = vec4(aPos.x, aPos.y, 0.0f, 1.0f);
}

colhouse.frag

//片段着色器，接收颜色并绘制
#version 330 core
out vec4 FragColor;
in vec3 fColor;

void main(){
  FragColor = vec4(fColor, 1.0f);
}

colhouse.geom 详情见代码注释

#version 330 core
layout (points) in;    //以点为单位进行扩张，每次从VertexShader往GeomShader传进一个点进行数据处理
layout (triangle_strip, max_vertices = 5) out; //将一个点变为五个可连成三角形的点 交给FragShader

out vec3 fColor;

in VS_OUT{      
  vec3 color;
} gs_in[]; //不管是从VertexShader传进来一个点，一条线，还是三角形，均是以数组的形式进行数据传递，所以实例的变量必须是数组

void buildHouse(vec4 position){
  fColor = gs_in[0].color;                              
  gl_Position = position + vec4(-0.2f, -0.2f, 0.0f, 0.0f);
  EmitVertex();                 //填充一个有了坐标和颜色的点

  gl_Position = position + vec4( 0.2f, -0.2f, 0.0f, 0.0f);
  EmitVertex();                 //再填充一个点，这个点继承上一个点的颜色，这一块类似于固定管线版本的状态机 机制

  gl_Position = position + vec4(-0.2f,  0.2f, 0.0f, 0.0f);
  EmitVertex();

  gl_Position = position + vec4( 0.2f,  0.2f, 0.0f, 0.0f);
  EmitVertex();

  gl_Position = position + vec4( 0.0f,  0.4f, 0.0f, 0.0f);
  fColor = vec3(1.0f, 1.0f, 1.0f);       // 更改点的颜色，再填充
  EmitVertex();

  EndPrimitive();          //结束点的填充
}

void main(){
  buildHouse(gl_in[0].gl_Position); //gl_in[]是内建变量，表示从顶点着色器传进来的数据，格式大致情况下应该如下
}

/*
 * in gl_Vertex
 * {
 *   vec4  gl_Position;
 *   float gl_PointSize;
 *   float gl_ClipDistance[];
 * } gl_in[];
 */

几何着色器注意事项：

1. 从顶点着色器传进来的数据都是以数组的形式进行保存
2. 填充点时，类似于状态机机制，比如颜色状态一经声明，将持续至下一次新颜色的声明。

在几何着色器中，处了图元points可作为顶点着色器输入类型，还有以下类型可以进行输入：

同理，输出接受以下三种类型：

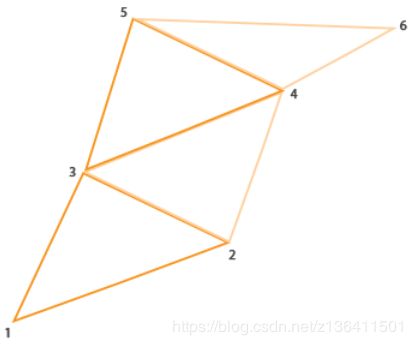
关于triangle_strip类型，有必要说明一下，传进来6个点，会生成4个三角形，顺序为（1，2，3），（2，3，4）（3，4，5），（4，5，6）

二. 特效制作

  这里Vries提供了两种特效制作思路：

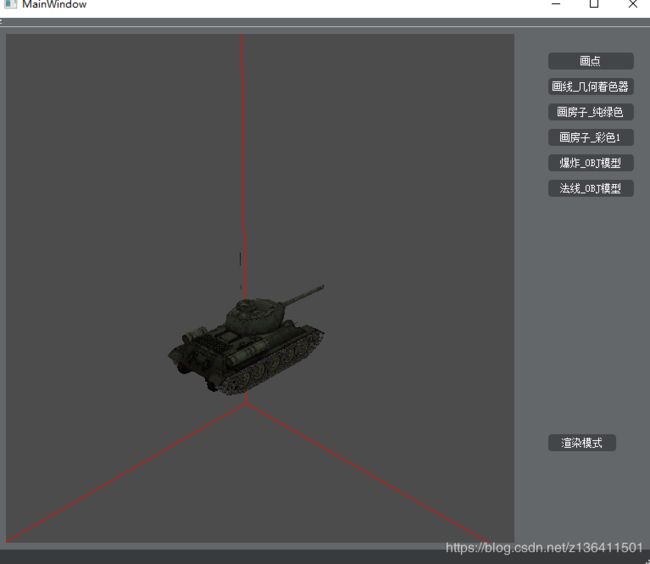
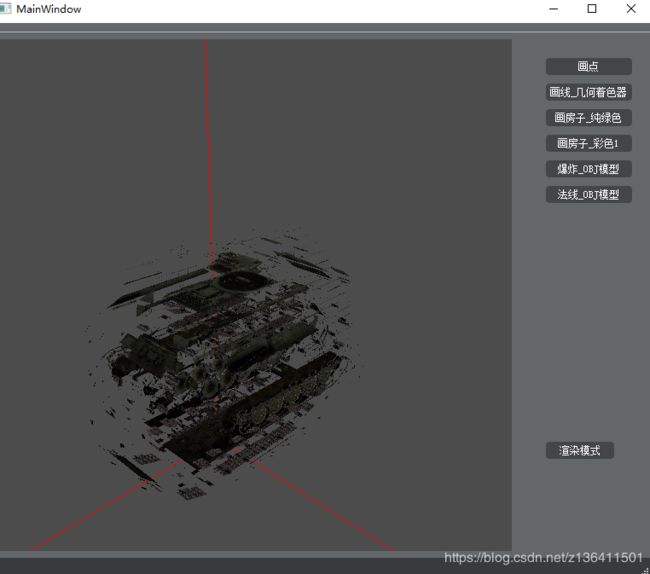
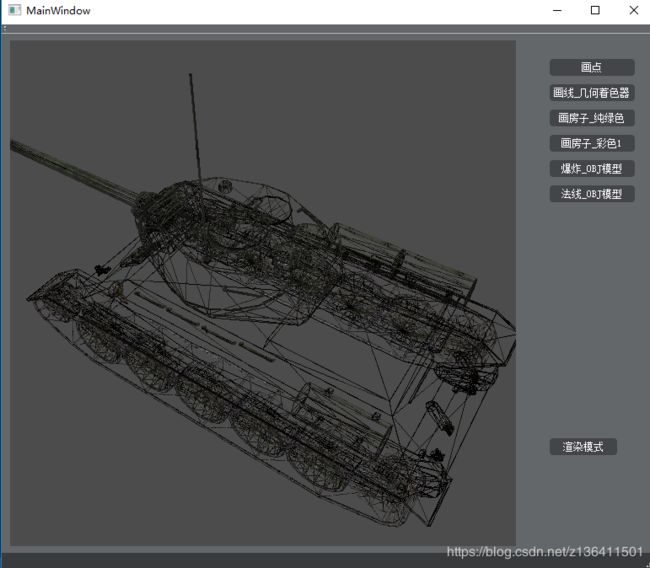
  2.1 爆炸

简单来说，我们都知道模型，是由多个三角形面组成的，每个三角形由三个矢量组成，而其中任两个矢量进行叉乘计算，就可以得到垂直于这个三角形面的法线。所以爆炸的原理，就是在几何着色器中将这个三角形面沿这个这个面法线的方向移动一定的距离，就这么简单。

这里只贴下几何着色器代码，当然，因为我的obj读取模型程序是我自己写的（之前教程有源代码讲解），所以略微修改了一点点的Vries代码。

#version 330 core
layout (triangles) in;              //传进有3个点构建的三角形
layout (triangle_strip, max_vertices = 3) out;  //同样传出由3个点构成的三角形

in VS_OUT{
  vec2 texCoords;
  vec3 fragPos;
  vec3 normal;
} gs_in[];


out vec2 TexCoords;
out vec3 FragPos;
out vec3 Normal;

uniform float time;

vec3 getNormal(){             //矢量叉乘算法线
  vec3 a = vec3(gl_in[0].gl_Position) - vec3(gl_in[1].gl_Position);
  vec3 b = vec3(gl_in[2].gl_Position) - vec3(gl_in[1].gl_Position);
  return normalize(cross(a, b));
}

vec4 explode(vec4 position, vec3 normal1){      //将三角形面沿法线距离前进一点点，这里用sin()函数，是因为可以将时间传进来，做成爆炸动画
  float magnitude = 2.0f;
  vec3 direction = normal1 * ((sin(time) + 1.0f)/2.0f) * magnitude;
  return position + vec4(direction, 1.0f);
}


void main(){
  vec3 normal = getNormal();

  gl_Position = explode(gl_in[0].gl_Position, normal);
  TexCoords = gs_in[0].texCoords;
  FragPos = gs_in[0].fragPos;
  Normal = gs_in[0].normal;
  EmitVertex();

  gl_Position = explode(gl_in[1].gl_Position, normal);
  TexCoords = gs_in[1].texCoords;
  FragPos = gs_in[1].fragPos;
  Normal = gs_in[1].normal;
  EmitVertex();

  gl_Position = explode(gl_in[2].gl_Position, normal);
  TexCoords = gs_in[2].texCoords;
  FragPos = gs_in[2].fragPos;
  Normal = gs_in[2].normal;
  EmitVertex();

  EndPrimitive();
}

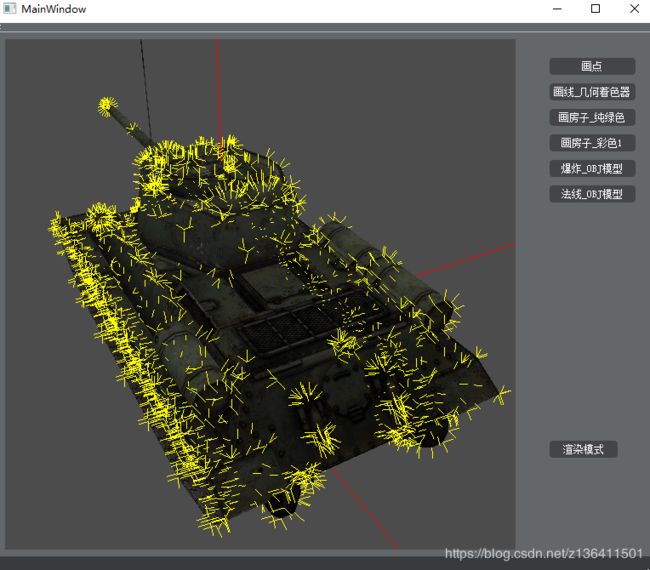
2.2 法向量可视化

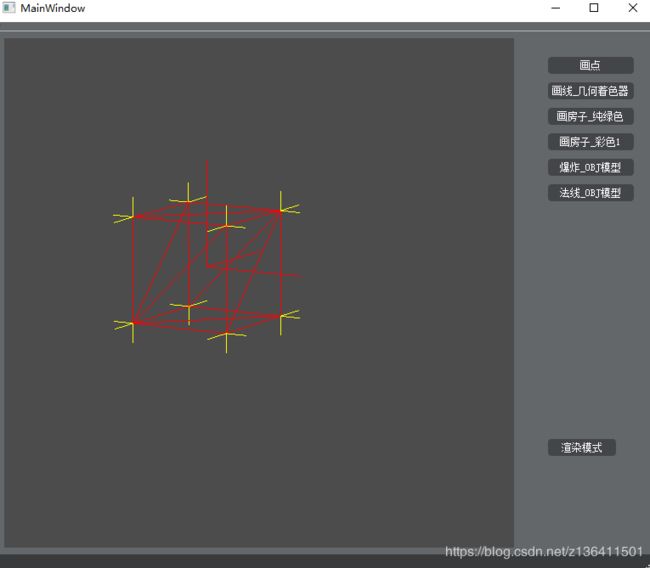
  这个实例可用来检测手动传进顶点着色器的法线，是否正确。比如下述这个立方体例子，我们可以通过几何着色器验证法线是否计算成功。

 float vertices[] = {
    // positions        // textures        // normals
    //Back Face
    -0.5f, -0.5f, -0.5f,  0.0f,  0.0f,  0.0f,  0.0f, -1.0f, //bottom-left
     0.5f,  0.5f, -0.5f,  1.0f,  1.0f,  0.0f,  0.0f, -1.0f, //top-right
     0.5f, -0.5f, -0.5f,  1.0f,  0.0f,  0.0f,  0.0f, -1.0f,
     0.5f,  0.5f, -0.5f,  1.0f,  1.0f,  0.0f,  0.0f, -1.0f,
    -0.5f, -0.5f, -0.5f,  0.0f,  0.0f,  0.0f,  0.0f, -1.0f,
    -0.5f,  0.5f, -0.5f,  0.0f,  1.0f,  0.0f,  0.0f, -1.0f,

    //Front Face
    -0.5f, -0.5f,  0.5f,  0.0f,  0.0f,  0.0f,  0.0f,  1.0f,
     0.5f, -0.5f,  0.5f,  1.0f,  0.0f,  0.0f,  0.0f,  1.0f,
     0.5f,  0.5f,  0.5f,  1.0f,  1.0f,  0.0f,  0.0f,  1.0f,
     0.5f,  0.5f,  0.5f,  1.0f,  1.0f,  0.0f,  0.0f,  1.0f,
    -0.5f,  0.5f,  0.5f,  0.0f,  1.0f,  0.0f,  0.0f,  1.0f,
    -0.5f, -0.5f,  0.5f,  0.0f,  0.0f,  0.0f,  0.0f,  1.0f,
            .........................

验证结果如下图所示，可以确定立方体法线计算正确。

  这个着色器的设计原理也很简单，在几何着色器中接收一个三角形面（因为obj的绘制方法draw是以triangles为单位的），传出去由三条由两个点组成的线，将传进的点沿法线方向延长一定距离即可。

objnormal.geom

#version 330 core
layout (triangles) in;
layout (line_strip, max_vertices = 6) out;

in VS_OUT {
    vec3 normal;
} gs_in[];

const float MAGNITUDE = 0.4;

void GenerateLine(int index)
{
    gl_Position = gl_in[index].gl_Position;
    EmitVertex();
    gl_Position = gl_in[index].gl_Position + vec4(gs_in[index].normal, 0.0) * MAGNITUDE;
    EmitVertex();
    EndPrimitive();
}

void main()
{
    GenerateLine(0); // 第一个顶点法线
    GenerateLine(1); // 第二个顶点法线
    GenerateLine(2); // 第三个顶点法线
}

objnormal.vert

#version 420 core
layout (location = 0) in vec3 aPos;
layout (location = 1) in vec2 aTex;
layout (location = 2) in vec3 aNormal;

layout(std140, binding = 0) uniform Matrices{
  uniform mat4 projection;
  uniform mat4 view;
};

uniform mat4 model;

out VS_OUT{
  vec3 normal;
} vs_out;


void main(){
  gl_Position = projection * view * model * vec4(aPos, 1.0f);
  mat3 normalMatrix = mat3(transpose(inverse(view * model)));
  vs_out.normal = normalize(vec3(projection * vec4(normalMatrix * aNormal, 0.0)));

}

这里我想说以下关于法线的传递，在以往传递真实法线时，比如计算光照所采用的法线，如下所示，将法线移动至世界坐标，同时使用mat3()矩阵去除位移的影响，transpose(inverse())去除不等比缩放的影响，仅保留旋转与等比缩放的影响即可。

  Normal = normalize(mat3(transpose(inverse(model))) * aNormal);

而在法线可视化着色器中，与光照计算时只需考虑法线的世界坐标位置不同，我们传递法线应该考虑view与projection矩阵，因为这时的法线需要可视化处理，如果只考虑model矩阵对法线的影响，我们在不同角度观察绘出的法线时只会是歪曲扭八的。