机器学习(6): 决策树算法 小结与实验

注：转载请标明原文出处链接：https://xiongyiming.blog.csdn.net/article/details/96630813

1 决策树算法简介

决策树(Decision Tree) 是在已知各种情况发生概率的基础上，通过构成决策树来求取净现值的期望值大于等于零的概率，评价项目风险，判断其可行性的决策分析方法，是直观运用概率分析的一种图解法。由于这种决策分支画成图形很像一棵树的枝干，故称决策树。在机器学习中，决策树是一个预测模型，它代表的是对象属性与对象值之间的一种映射关系。Entropy = 系统的凌乱程度，使用算法ID3, C4.5和C5.0生成树算法使用熵。这一度量是基于信息学理论中熵的概念。
决策树是一种树形结构，其中每个内部节点表示一个属性上的测试，每个分支代表一个测试输出，每个叶节点代表一种类别。
(以上均来自百度百科)

决策树学习算法的最大优点是，它可以自学习。在学习的过程中，不需要使用者了解过多背景知识，只需要对训练实例进行较好的标注，就能够进行学习。显然，它属于有监督学习。从一类无序、无规则的事物(概念)中推理出决策树表示的分类规则。

2 决策树算法

分类决策树模型是一种描述对实例进行分类的树形结构。决策树由结点和有向边组成。结点有三种类型：根节点、内部结点和叶节点。
根结点：包含全部样本;
叶结点：对应决策的结果;
内部结点：对应属性测试.

2.1 引例

例1

决策树分类的思想类似于找对象。现想象一个女孩的母亲要给这个女孩介绍男朋友，于是有了下面的对话：
女儿：多大年纪了？ (年龄)
母亲：26。
女儿：长的帅不帅？ (长相)
母亲：挺帅的。
女儿：收入高不？ (收入情况)
母亲：不算很高，中等情况。
女儿：是公务员不？ (是否公务员)
母亲：是，在税务局上班呢。
女儿：那好，我去见见。

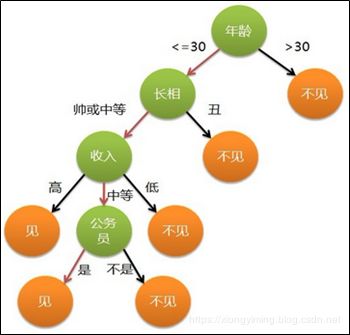
那么以上的对话女儿的最终决定是见，其中，叶节点就是“见”和“不见” ，内部节点就是：年龄、长相、收入情况和公务员。
其决策树如下图所示：

例2

机器学习中的西瓜数据集如下：

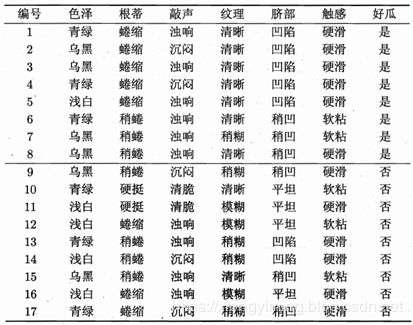
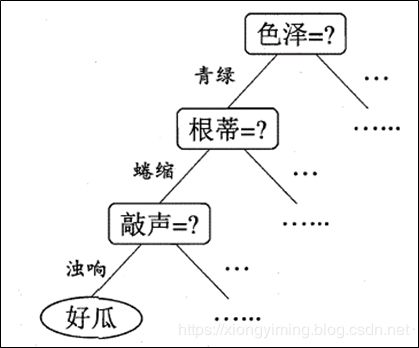
由上面西瓜数据集可知，由17个样本，对应6中属性(色泽、根蒂、敲声、纹理，脐部和触感)和最终的结果是不是好瓜。那么叶节点就是“好瓜”和“坏瓜” ，内部节点就是：色泽、根蒂、敲声、纹理，脐部和触感。
决策树的判别类似于人在面临问题决策的问题时的处理机制。我们通常买西瓜会看习惯的颜色，新鲜感，敲一敲是什么声音等。通过这几个问题，最终我们会做出决策，这个是不是好瓜。
其决策树如下图所示：

2.2 算法分类

决策树算法流程如下：

咋一眼，看着上面的算法比较复杂。其实决策树的生成就是一个递归过程。下面以西瓜数据集为例，进行计算。
一般而言，我们希望决策树的分支点所包含的样本尽可能属于同一类别，也就是节点的纯度(purity) 越来越高。在样本集中属性都会编码为一些数字(1，-1等)，如何从这些数字进行划分呢？ 在实际使用中，我们衡量的常常是不纯度。度量不纯度的指标有很多，例如：信息熵，信息增益，增益率，基尼指数等。也就是通过信息熵，信息增益，增益率，基尼指数等对样本中的数字进行划分。

(1) 信息熵

信息熵定义表示随机变量不确定性的度量，假设有当前样本集合D中第k被样本所占的比例为 ，则$D$的信息熵定义为$p_k(k=1,2,\dots ,\left|y\right|)$，则$D$的信息熵定义为
$$\mathrm{E}\mathrm{n}\mathrm{t}(D)=-\sum _{k=1}^{|y|}{p}_k{\log }_2{p}_k\text{\hspace{1em}(1)}$$
其中， $\mathrm{E}\mathrm{n}\mathrm{t}(D)$的值越小，则$D$的纯度越高。

下面计算生成数据集然后计算熵（以机器学习实战书上的海洋生物数据为例）。

1. 函数calEnt()计算熵
2. 函数createDataSet()生成数据集

代码示例

import numpy as np
import pandas as pd

# calEnt 函数功能：计算熵
# 参数说明：
#     dataSet：原始数据集
# 返回：
#     ent:熵的值
# """
def calEnt(dataSet):
    n = dataSet.shape[0] #数据集总行数
    iset = dataSet.iloc[:,-1].value_counts() #标签的所有类别
    p = iset/n #每一类标签所占比
    ent = (-p*np.log2(p)).sum() #计算信息熵
    return ent


#createDataSet 函数功能: 创建数据集
def createDataSet():
    row_data = {'no surfacing':[1,1,1,0,0],
    'flippers':[1,1,0,1,1],
    'fish':['yes','yes','no','no','no']}
    dataSet = pd.DataFrame(row_data)
    return dataSet


# 调用
dataSet = createDataSet() # 调用创建数据集 函数
result_calEnt=calEnt(dataSet)# 调用计算熵 函数
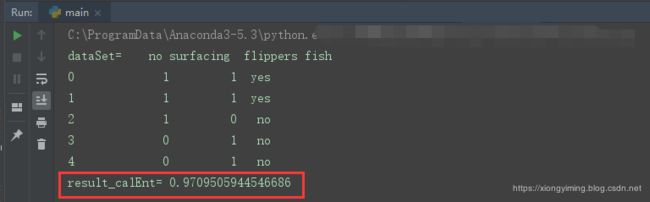
print("dataSet=",dataSet)
print("result_calEnt=",result_calEnt)

运行结果如下

注：熵越高，信息的不纯度就越高，即数据越混乱。

(2) 信息增益

信息增益的计算其实就是父节点的信息熵与下面所有节点总信息熵之差。但是不是简单地这里的子节点的总信息熵不能简单地求和，需要在求和前进行修正。
假设离散属性$a$有$V$个可能的取值 $\left\{a^1,a^2,\dots ,a^V\right\}$，若使用属性a对样本集D进行划分，则会产生$V$个分直接点，其中第$v$个分直接点包含了$D$中所有在属性$a$上取值为 $a^V$的样本，记为 $D^V$。我们可以通过公式(1)计算 $D^V$的信息熵，再考虑到不同的分支点所办函的样本数不同，给分支点赋予权重 $\left|D^V\right|/\left|D\right|$，则样本数越多的分支节点的影响最大，于是可以计算出用属性$a$对样本集$D$进行划分所获得的信息增益为：
$$\mathrm{G}\mathrm{a}\mathrm{i}\mathrm{n}(D,\mathrm{a})=\mathrm{E}\mathrm{n}\mathrm{t}(D)-\sum _{v=1}^V\frac{\left|D^v\right|}{\left|D\right|}\mathrm{E}\mathrm{n}\mathrm{t}(D^v)\text{\hspace{1em}(2)}$$
其中，信息增益越大，则意味着用属性a来进行划分所获得的纯度提升越大。
著名的ID3(Iterative Dichotomiser, 迭代二分器) 决策树学习算法就是以信息增益为准则来划分属性。
下面使用信息增益在西瓜数据集生成决策树。

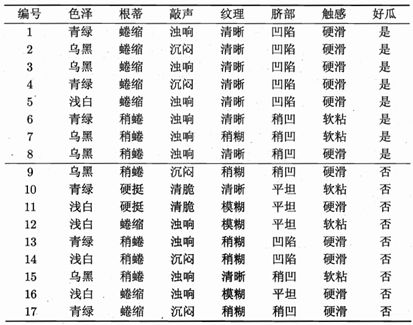
首先计算根节点的信息熵
$$\mathrm{E}\mathrm{n}\mathrm{t}(D)=-\sum _{k=1}^{|y|}{p}_k{\log }_2{p}_k=-(\frac{8}{17}{\log }_2\frac{8}{17}+\frac{9}{17}{\log }_2\frac{9}{17})=0.998$$
然后计算当前属性集合(色泽、根蒂、敲声、纹理，脐部和触感)中每个属性的信息增益。属性“色泽”有三个属性(青绿，乌黑，浅白)。若使用该属性对数据集D进行划分，则可以得到3个子集，分别记为： $D^1$(色泽=青绿)， $D^2$(色泽=乌黑)， $D^2$(色泽=浅白)
子集 $D^1$包含编号为(1,4,6,10,13,17)的6个样例，其中好瓜占$p_1=\frac{3}{6}$，坏瓜占 $p_2=\frac{3}{6}$；同理子集 $D^2$中，好瓜占 $p_1=\frac{4}{6}$，坏瓜占 $p_1=\frac{2}{6}$；子集 $D^3$中，好瓜占 $p_1=\frac{1}{5}$，坏瓜占 $p_1=\frac{4}{5}$。则，根据公式(1)可以计算用属性色泽划分后所获得的3个分支节点的信息熵为
$$\mathrm{E}\mathrm{n}\mathrm{t}(D^1)=-(\frac{3}{6}{\log }_2\frac{3}{6}+\frac{3}{6}{\log }_2\frac{3}{6})=1$$ $$\mathrm{E}\mathrm{n}\mathrm{t}(D^2)=-(\frac{4}{6}{\log }_2\frac{4}{6}+\frac{2}{6}{\log }_2\frac{2}{6})=0.918$$ $$\mathrm{E}\mathrm{n}\mathrm{t}(D^3)=-(\frac{1}{5}{\log }_2\frac{1}{5}+\frac{4}{5}{\log }_2\frac{4}{5})=0.722$$
则，根据公式(2)可以计算属性色泽的信息增益为
$$\mathrm{G}\mathrm{a}\mathrm{i}\mathrm{n}(D,a_1)=\mathrm{E}\mathrm{n}\mathrm{t}(D)-\sum _{v=1}^3\frac{\left|D^v\right|}{\left|D\right|}\mathrm{E}\mathrm{n}\mathrm{t}(D^v)=0.998-(\frac{6}{17}\times 1+\frac{6}{17}\times 0.918+\frac{5}{17}\times 0.722)=0.109$$
同理可以计算出其他属性的信息增益(色泽、根蒂、敲声、纹理，脐部和触感分别用 $a_1,a_2,a_3,a_4,a_5,a_6$表示)，则
$$\mathrm{G}\mathrm{a}\mathrm{i}\mathrm{n}(D,a_2)=0.143$$ $$\mathrm{G}\mathrm{a}\mathrm{i}\mathrm{n}(D,a_3)=0.141$$ $$\mathrm{G}\mathrm{a}\mathrm{i}\mathrm{n}(D,a_4)=0.381$$ $$\mathrm{G}\mathrm{a}\mathrm{i}\mathrm{n}(D,a_5)=0.289$$ $$\mathrm{G}\mathrm{a}\mathrm{i}\mathrm{n}(D,a_6)=0.006$$
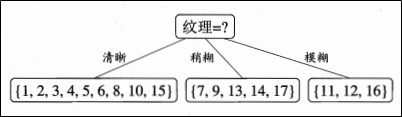
显然，属性纹理使的信息增益最大，于是被选为划分属性，下图为基于纹理对根节点进行划分的结果。

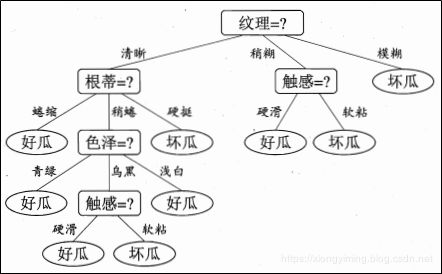
然后决策树学习算法将每一个节点做进一步划分，最终得到决策树如下图所示

(3) 增益率

实际中，信息增益准则对可取值数目较多的属性有所偏好，为了减少这种偏好对决策树带来不利影响，C4.5决策树算法不直接使用信息增益，而是使用增益率来选择最优划分属性，增益率定义为
$$\mathrm{G}\mathrm{a}\mathrm{i}\mathrm{n}\_\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}(D,\mathrm{a})=\frac{\mathrm{G}\mathrm{a}\mathrm{i}\mathrm{n}(D,a)}{\mathrm{I}\mathrm{V}(a)}\text{\hspace{1em}(3)}$$
其中 $\mathrm{I}\mathrm{V}(a)$定义为：
$$\mathrm{I}\mathrm{V}(a)=-\sum _{v=1}^V\frac{\left|D^v\right|}{\left|D\right|}\mathrm{l}\mathrm{o}{\mathrm{g}}_2\frac{\left|D^v\right|}{\left|D\right|}\text{\hspace{1em}(4)}$$
$\mathrm{I}\mathrm{V}(a)$称为属性$a$的固有值。属性$a$的可能取值数目越多(V越大)，则 $\mathrm{I}\mathrm{V}(a)$的值通常越大。增益率准则对可取值数目较少的属性有所偏好，因此C4.5算法并不是直接选择增益率最大的候选划分属性，而是使用一个启发式：先从候选划分属性中找出信息增益高于平均水平的属性，再从中选择增益最高的。

(4) 基尼指数

CART(Classification and Regression Tree) 决策树使用基尼指数(Gini index)来选择划分属性，则数据集$D$的纯度用基尼值定义为
$$\mathrm{G}\mathrm{i}\mathrm{n}\mathrm{i}(D)=\sum _{k=1}^{|y|}\sum _{k^{\prime }̸=k}{p}_k{p}_{k^{\prime }}=1-\sum _{k=1}^{|y|}{p}_k^2\text{\hspace{1em}(5)}$$
$\mathrm{G}\mathrm{a}\mathrm{i}\mathrm{n}(D)$反映了从数据集D中随机抽取两个样本，其类别标记不一致的概率。因此， $\mathrm{G}\mathrm{a}\mathrm{i}\mathrm{n}(D)$越小，数据集$D$的纯度越高。
故，属性$a$的基尼指数定义为
$$\mathrm{G}\mathrm{i}\mathrm{n}\mathrm{i}\_\mathrm{i}\mathrm{n}\mathrm{d}\mathrm{e}\mathrm{x}(D,a)=\sum _{k=1}^{|y|}\frac{\left|D^v\right|}{\left|D\right|}\mathrm{G}\mathrm{i}\mathrm{n}\mathrm{i}(D^v)\text{\hspace{1em}(6)}$$
于是，我们选择在候选属性集合$A$中，选择那么使得划分后基尼指数最小的属性作为最优划分属性，
即 $a_{\ast }=\underset{a\in A}{\arg }\mathrm{G}\mathrm{i}\mathrm{n}\mathrm{i}\_\mathrm{i}\mathrm{n}\mathrm{d}\mathrm{e}\mathrm{x}(D,a)$

3 决策树算法优缺点

优点：计算复杂度不高，输出结果易于理解，对中间值的缺失不敏感，可以处理不相关特征数据；
缺点：可能会产生过度匹配问题；
适用数据范围：数值型和标称型。

4 实验

以机器学习实战书中的数据为例

trees.py

#trees.py
from math import log
import operator

def createDataSet():  #创建数据
    dataSet = [[1, 1, 'yes'],
               [1, 1, 'yes'],
               [1, 0, 'no'],
               [0, 1, 'no'],
               [0, 1, 'no']]
    #labels = ['no surfacing','flippers']
    labels = ['不浮出水面', '脚蹼']
    #change to discrete values
    return dataSet, labels

def calcShannonEnt(dataSet): #计算熵
    numEntries = len(dataSet)
    labelCounts = {}
    for featVec in dataSet: #the the number of unique elements and their occurance
        currentLabel = featVec[-1]
        if currentLabel not in labelCounts.keys(): labelCounts[currentLabel] = 0
        labelCounts[currentLabel] += 1
    shannonEnt = 0.0
    for key in labelCounts:
        prob = float(labelCounts[key])/numEntries
        shannonEnt -= prob * log(prob,2) #log base 2
    return shannonEnt
    
def splitDataSet(dataSet, axis, value): # 划分数据
    retDataSet = []
    for featVec in dataSet:
        if featVec[axis] == value:
            reducedFeatVec = featVec[:axis]     #chop out axis used for splitting
            reducedFeatVec.extend(featVec[axis+1:])
            retDataSet.append(reducedFeatVec)
    return retDataSet
    
def chooseBestFeatureToSplit(dataSet): # 选择最好的方式划分数据集(利用信息增益)
    numFeatures = len(dataSet[0]) - 1      #the last column is used for the labels
    baseEntropy = calcShannonEnt(dataSet)
    bestInfoGain = 0.0; bestFeature = -1
    for i in range(numFeatures):        #iterate over all the features
        featList = [example[i] for example in dataSet]#create a list of all the examples of this feature
        uniqueVals = set(featList)       #get a set of unique values
        newEntropy = 0.0
        for value in uniqueVals:
            subDataSet = splitDataSet(dataSet, i, value)
            prob = len(subDataSet)/float(len(dataSet))
            newEntropy += prob * calcShannonEnt(subDataSet)     
        infoGain = baseEntropy - newEntropy     #calculate the info gain; ie reduction in entropy
        if (infoGain > bestInfoGain):       #compare this to the best gain so far
            bestInfoGain = infoGain         #if better than current best, set to best
            bestFeature = i
    return bestFeature                      #returns an integer

def majorityCnt(classList):
    classCount={}
    for vote in classList:
        if vote not in classCount.keys(): classCount[vote] = 0
        classCount[vote] += 1
    sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True)
    return sortedClassCount[0][0]

def createTree(dataSet,labels): # 创建树
    classList = [example[-1] for example in dataSet]
   

main.py

# main.py
from numpy import *
import trees
import treePlotter
import matplotlib.pyplot as plt
myData, labels=trees. createDataSet() # 读取数据
print(myData) # 打印数据

entropy=trees.calcShannonEnt(myData) #计算熵
print(entropy)

result=trees.chooseBestFeatureToSplit(myData) #利用信息增益得到决策树
print(result)
result_Tree=trees.createTree(myData, labels)
print(result_Tree)

运行结果如下

---

参考资料

[1] 机器学习实战. 人民邮电出版社.
[2] https://coding.imooc.com/class/chapter/169.html#Anchor
[3] 机器学习, 北京: 清华大学出版社, 2016年1月
[4] 机器学习(西瓜书). 公式推导解析