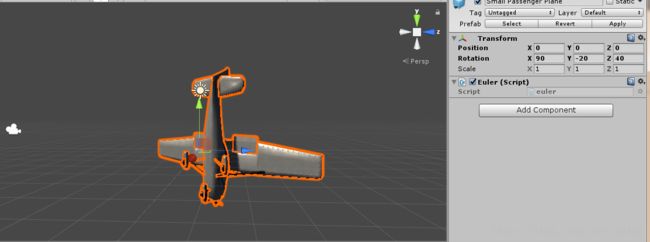
初识欧拉角与万向节死锁

定义

先引wiki上的定义
欧拉角：由三个角度组成，在特定坐标系下用于描述刚体的orientation.

简单来说，就是绕一个三维坐标系统下的三个基轴旋转三个角度，可以用来表示物体通过各种绕七绕八的转，最终转到的那种形态（orientation）。

这里的orientation我不知道该怎么翻译，指的是物体的“朝向“，但绝对不是指一个方向（direction）或者我们说的向量（vector），或许用“物体姿态“来描述orientation更好。


当你旋转一个向量时，向量是不会改变的，因为向量没有orientation这个属性

而当你旋转一个物体时，你就会改变这个物体的orientation

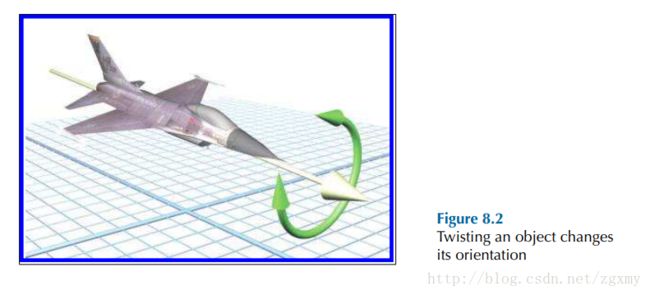
我个人想把orientation翻译为“旋向”，指物体旋转的方向。（雾）

表示一个方向，我们不一定要用向量，向量包含了多余的长度信息，所以最少只需要两个角度就够了（三维极坐标系）
而表示一个旋向 orientation，或者说物体姿态，用变量最少的欧拉角也需要用到三个角度
从变量个数来看， 自然的，向量与orientation不同。整整差了个维度呢。

欧拉角可以表示任意的orientation，当你在Unity里的inspector面板里调节rotation的时候，其实你也是在调节一个欧拉角（后文再提）。

希望这段文字可以讲清楚什么是orientation，并请务必搞清楚什么是orientation，让我们继续。

分类

欧拉角按旋转的坐标系分为内旋（intrinsic rotation）和外旋（extrinsic rotation）。
按旋转轴分为经典欧拉角（Proper Euler Angle）和泰特布莱恩角（Tait–Bryan angles）。
本文中我们用(φ, θ, ψ)（轴序，zyx） 来描述一个欧拉角

经典欧拉角（Proper Euler Angle）

按(z-x-z, x-y-x, y-z-y, z-y-z, x-z-x, y-x-y)轴序列旋转，即第一个旋转轴和最后一个旋转轴相同

泰特布莱恩角（Tait–Bryan angles）

按(x-y-z, y-z-x, z-x-y, x-z-y, z-y-x, y-x-z)轴序列旋转，即三个不同的轴

内旋（intrinsic rotation）

绕物体自身的坐标系object-space 旋转，举个例子，一个(φ, θ, ψ) （xyz，instrinsic）的欧拉角，指绕物体的x轴转φ后，再绕物体的y’轴（这里用y’表示这个新的y轴已经和一开始世界坐标系下的那个物体的y轴不一样了）旋转θ，最后绕z’轴旋转φ，每一次旋转都会改变下一次旋转的轴。这种情况下旋转的轴是动态（moving axis）的。

下图引自wiki，一个zxz的内旋

外旋（extrinsic rotation）

绕惯性系upright-space 旋转（upright space指基向量平行于world-space或parent-space，原点与object-space的原点重合的空间）。
也就说，无论是三步旋转中的哪一步，轴都是固定的，是不会动的。
unity中的rotation就是一种外旋。

一个rotation为（0,0,30）的飞机

旋转到（0,90,0）,可以看到飞机并没有沿着旋转后的y轴（灰色箭头）旋转，仍然依照世界坐标系下的y轴（红色箭头）旋转

yaw-pitch-row（heading-pitch-bank）

我们把（z,y,x 内旋（intrinsic））的这种格式称为 yaw-pitch-roll(heading-pitch-bank)

下图引自wiki，yaw pitch & orw

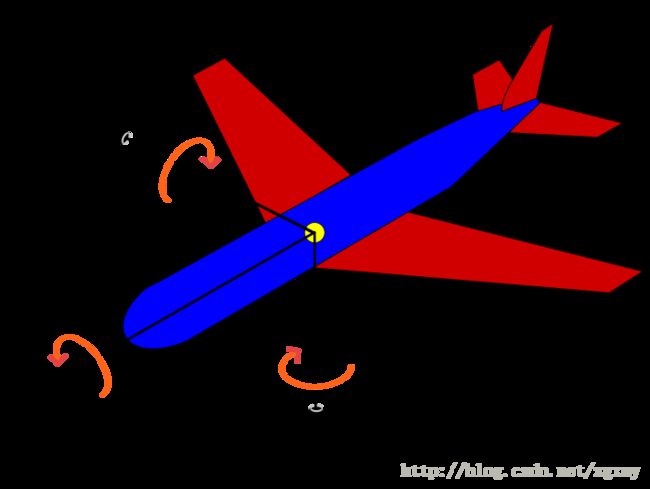
图中的绿色箭头为yaw(heading)，红色箭头为pitch，蓝色箭头为row(bank)

关于unity中的欧拉角

我本来想自己写的，可惜已经有人写过了
这个帖子写的很好，看这个就行了
http://blog.csdn.net/andrewfan/article/details/60866636

关于万向节死锁（gimbal lock）

同样的，看andrewfan的这个帖子就行了，讲的挺清楚
http://blog.csdn.net/andrewfan/article/details/60981437
关于万向节死锁，我再赘述一下
Unity中的rotation是(φ, θ, ψ) （zxy ，外旋(extrinsic)），也就是说，当我先绕世界坐标z轴旋转40，再绕世界坐标x轴旋转90，最后绕世界坐标y轴旋转-20的结果（40,90,-20）
和先绕世界坐标z轴旋转60，再绕世界坐标x轴旋转90的结果（60,90,0）的结果是一样的
（补充一下，旋转的方向由坐标系决定，比如图中是左手系，就按左手螺旋来判定旋转方向。）
这里看到两种欧拉角旋转的结果是等价的，并且当x旋转90度时，任意的（a,90,b）都能用（a-b,90,0）来描述。此时我们称z轴失去了自由度，并称这种情况为万向节死锁
个人觉得这种现象是因为欧拉角表示一个orientation的的不唯一性引起的，这也欧拉角没办法做插值的主要原因。
具体还是看上面的帖子吧