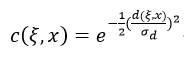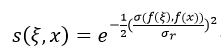Opencv2.4.9源码分析——adaptiveBilateralFilter
上一篇文章我们介绍了双边滤波,它的公式为:
![]() (1)
(1)
c(ξ,x)表示的是高斯距离的权值,σd值大则滤波结果会受到更远的像素影响;s(ξ,x)表示的是高斯相似度的权值,σr值大则意味着更无关的像素强度值(或颜色值)会影响滤波器结果。因此这两个值的选取会直接影响到滤波效果。
关于高斯距离的权值,还会受到滤波内核大小的影响,因此它的方差σd值对滤波结果的影响会受到一定的约束,但σr值的选取就难以把握,因此本算法的目的就是自适应的选取σr值的大小。
在opencv文档中没有说明该算法的出处,但从它的程序源码中可以分析得到,σ r值是通过领域内的像素值得到,具体公式为:其中,n表示邻域内的像素个数,该邻域指的是滤波内核,I(i)表示的是像素值。
下面我们来分析一下具体的代码,该函数的原型为:
void adaptiveBilateralFilter(InputArraysrc, OutputArray dst, Size ksize, double sigmaSpace, double maxSigmaColor=20.0,Point anchor=Point(-1, -1), int borderType=BORDER_DEFAULT )
_src为输入原图像;_dst为滤波后的图像;ksize为滤波内核的大小;sigmaSpace为距离权值公式中的方差,即公式1中的σd;maxSigmaColor为相似度权值公式中的方差(σr)的最大值,自适应双边滤波的相似度方差是通过公式2计算得到,但如果计算的结果太大,超过了该值,则以该值为准;anchor为内核锚点;borderType表示用什么方式来处理加宽后的图像四周边界。
该函数的源码是在/sources/modules/imgproc/scr/smooth.cpp内:
void cv::adaptiveBilateralFilter( InputArray _src, OutputArray _dst, Size ksize,
double sigmaSpace, double maxSigmaColor, Point anchor, int borderType )
{
//得到输入图像矩阵和与其尺寸类型一致的输出图像矩阵
Mat src = _src.getMat();
_dst.create(src.size(), src.type());
Mat dst = _dst.getMat();
//该算法只能处理8位二进制的灰度图像和三通道的彩色图像
CV_Assert(src.type() == CV_8UC1 || src.type() == CV_8UC3);
//得到滤波内核的锚点
anchor = normalizeAnchor(anchor,ksize);
if( src.depth() == CV_8U )
adaptiveBilateralFilter_8u( src, dst, ksize, sigmaSpace, maxSigmaColor, anchor, borderType );
else
CV_Error( CV_StsUnsupportedFormat,
"Adaptive Bilateral filtering is only implemented for 8u images" );
}
static void adaptiveBilateralFilter_8u( const Mat& src, Mat& dst, Size ksize, double sigmaSpace, double maxSigmaColor, Point anchor, int borderType )
{
Size size = src.size();
////处理之前再次检查图像中的相关信息是否正确
CV_Assert( (src.type() == CV_8UC1 || src.type() == CV_8UC3) &&
src.type() == dst.type() && src.size() == dst.size() &&
src.data != dst.data );
//为了在图像边界处得到更好的处理效果,需要对图像四周边界做适当的处理
//把原图的四周都加宽,而加宽部分的像素值由borderType值决定
//待处理的图像由src换成了temp
Mat temp;
copyMakeBorder(src, temp, anchor.x, anchor.y, anchor.x, anchor.y, borderType);
//通过实例化adaptiveBilateralFilter_8u_Invoker类计算得到自适应双边滤波的结果
adaptiveBilateralFilter_8u_Invoker body(dst, temp, ksize, sigmaSpace, maxSigmaColor, anchor);
parallel_for_(Range(0, size.height), body, dst.total()/(double)(1<<16));
}
我们先看一下adaptiveBilateralFilter_8u_Invoker类的构造函数:
adaptiveBilateralFilter_8u_Invoker(Mat& _dest, const Mat& _temp, Size _ksize, double _sigma_space, double _maxSigmaColor, Point _anchor) :
temp(&_temp), dest(&_dest), ksize(_ksize), sigma_space(_sigma_space), maxSigma_Color(_maxSigmaColor), anchor(_anchor)
{
if( sigma_space <= 0 ) //确保σd值不能小于零
sigma_space = 1;
CV_Assert((ksize.width & 1) && (ksize.height & 1)); //确保滤波内核的宽和高是奇数
space_weight.resize(ksize.width * ksize.height);
double sigma2 = sigma_space * sigma_space;
int idx = 0;
int w = ksize.width / 2;
int h = ksize.height / 2;
//遍历整个内核,计算高斯距离权值
for(int y=-h; y<=h; y++)
for(int x=-w; x<=w; x++)
{
//在程序中定义了宏ABF_GAUSSIAN,因此高斯距离权值使用的是本文中给出的公式
#if ABF_GAUSSIAN
space_weight[idx++] = (float)exp ( -0.5*(x * x + y * y)/sigma2);
#else
space_weight[idx++] = (float)(sigma2 / (sigma2 + x * x + y * y));
#endif
}
}
virtual void operator()(const Range& range) const
{
int cn = dest->channels(); //得到图像的通道数,即是灰度图像还是彩色图像
int anX = anchor.x;
const uchar *tptr;
for(int i = range.start;i < range.end; i++)
{
int startY = i;
if(cn == 1) //灰度图像处理方法
{
float var; //方差
int currVal; //当前像素值
int sumVal = 0; //方差和
int sumValSqr = 0; //方差的平方和
int currValCenter; //当前内核中心的像素值,即待处理的像素值
int currWRTCenter; //像素的权值
float weight;
float totalWeight = 0.;
float tmpSum = 0.;
for(int j = 0;j < dest->cols *cn; j+=cn)
{
sumVal = 0;
sumValSqr= 0;
totalWeight = 0.;
tmpSum = 0.;
// Top row: don't sum the very last element
int startLMJ = 0;
int endLMJ = ksize.width - 1;
int howManyAll = (anX *2 +1)*(ksize.width ); //内核像素个数总和
//在程序前面定义了宏ABF_CALCVAR,因此执行#if的内容
#if ABF_CALCVAR
//遍历整个内核,计算高斯相似度权值的方差
for(int x = startLMJ; x< endLMJ; x++)
{
//内核中某个像素的指针
tptr = temp->ptr(startY + x) +j;
for(int y=-anX; y<=anX; y++)
{
currVal = tptr[cn*(y+anX)]; //像素值
sumVal += currVal; //像素之和
sumValSqr += (currVal *currVal); //像素平方之和
}
}
//由公式2得到方差
var = ( (sumValSqr * howManyAll)- sumVal * sumVal ) / ( (float)(howManyAll*howManyAll));
//如果计算得到的方差太小,则取值0.01
//如果计算得到的方差超过在调用该函数中所给定的方差,则以给定的方差为准
if(var < 0.01)
var = 0.01f;
else if(var > (float)(maxSigma_Color*maxSigma_Color) )
var = (float)(maxSigma_Color*maxSigma_Color) ;
#else
var = maxSigmaColor*maxSigmaColor;
#endif
startLMJ = 0;
endLMJ = ksize.width;
tptr = temp->ptr(startY + (startLMJ+ endLMJ)/2);
currValCenter =tptr[j+cn*anX]; //内核中心像素,即带处理的像素值
//再次遍历内核,这次是由公式1得到输出图像
for(int x = startLMJ; x< endLMJ; x++)
{
tptr = temp->ptr(startY + x) +j;
for(int y=-anX; y<=anX; y++)
{
#if ABF_FIXED_WEIGHT
weight = 1.0;
#else
currVal = tptr[cn*(y+anX)];
//内核领域内的像素与内核中心像素之差,
currWRTCenter = currVal - currValCenter;
//在程序前面定义了宏ABF_GAUSSIAN,因此利用高斯函数得到整个权值(距离权值和相似度权值)
#if ABF_GAUSSIAN
weight = exp ( -0.5f * currWRTCenter * currWRTCenter/var ) * space_weight[x*ksize.width+y+anX];
#else
weight = var / ( var + (currWRTCenter * currWRTCenter) ) * space_weight[x*ksize.width+y+anX];
#endif
#endif
//得到公式1中的分子部分
tmpSum += ((float)tptr[cn*(y+anX)] * weight);
//得到公式1中的分母部分
totalWeight += weight;
}
}
tmpSum /= totalWeight; //得到公式1的最终结果
//把结果赋值给输出图像
dest->at(startY ,j)= static_cast(tmpSum);
}
}
else // 处理彩色图像
{
assert(cn == 3);
float var_b, var_g, var_r;
int currVal_b, currVal_g, currVal_r;
int sumVal_b= 0, sumVal_g= 0, sumVal_r= 0;
int sumValSqr_b= 0, sumValSqr_g= 0, sumValSqr_r= 0;
int currValCenter_b= 0, currValCenter_g= 0, currValCenter_r= 0;
int currWRTCenter_b, currWRTCenter_g, currWRTCenter_r;
float weight_b, weight_g, weight_r;
float totalWeight_b= 0., totalWeight_g= 0., totalWeight_r= 0.;
float tmpSum_b = 0., tmpSum_g= 0., tmpSum_r = 0.;
for(int j = 0;j < dest->cols *cn; j+=cn)
{
sumVal_b= 0, sumVal_g= 0, sumVal_r= 0;
sumValSqr_b= 0, sumValSqr_g= 0, sumValSqr_r= 0;
totalWeight_b= 0., totalWeight_g= 0., totalWeight_r= 0.;
tmpSum_b = 0., tmpSum_g= 0., tmpSum_r = 0.;
// Top row: don't sum the very last element
int startLMJ = 0;
int endLMJ = ksize.width - 1;
int howManyAll = (anX *2 +1)*(ksize.width);
#if ABF_CALCVAR
float max_var = (float)( maxSigma_Color*maxSigma_Color);
//遍历内核,分别计算红、绿、蓝三个通道的相似度权值方差
for(int x = startLMJ; x< endLMJ; x++)
{
tptr = temp->ptr(startY + x) +j;
for(int y=-anX; y<=anX; y++)
{
currVal_b = tptr[cn*(y+anX)], currVal_g = tptr[cn*(y+anX)+1], currVal_r =tptr[cn*(y+anX)+2];
sumVal_b += currVal_b;
sumVal_g += currVal_g;
sumVal_r += currVal_r;
sumValSqr_b += (currVal_b *currVal_b);
sumValSqr_g += (currVal_g *currVal_g);
sumValSqr_r += (currVal_r *currVal_r);
}
}
var_b = ( (sumValSqr_b * howManyAll)- sumVal_b * sumVal_b ) / ( (float)(howManyAll*howManyAll));
var_g = ( (sumValSqr_g * howManyAll)- sumVal_g * sumVal_g ) / ( (float)(howManyAll*howManyAll));
var_r = ( (sumValSqr_r * howManyAll)- sumVal_r * sumVal_r ) / ( (float)(howManyAll*howManyAll));
if(var_b < 0.01)
var_b = 0.01f;
else if(var_b > max_var )
var_b = (float)(max_var) ;
if(var_g < 0.01)
var_g = 0.01f;
else if(var_g > max_var )
var_g = (float)(max_var) ;
if(var_r < 0.01)
var_r = 0.01f;
else if(var_r > max_var )
var_r = (float)(max_var) ;
#else
var_b = maxSigma_Color*maxSigma_Color; var_g = maxSigma_Color*maxSigma_Color; var_r = maxSigma_Color*maxSigma_Color;
#endif
startLMJ = 0;
endLMJ = ksize.width;
tptr = temp->ptr(startY + (startLMJ+ endLMJ)/2) + j;
currValCenter_b =tptr[cn*anX], currValCenter_g =tptr[cn*anX+1], currValCenter_r =tptr[cn*anX+2];
//再次遍历内核,计算最终的结果
for(int x = startLMJ; x< endLMJ; x++)
{
tptr = temp->ptr(startY + x) +j;
for(int y=-anX; y<=anX; y++)
{
#if ABF_FIXED_WEIGHT
weight_b = 1.0;
weight_g = 1.0;
weight_r = 1.0;
#else
currVal_b = tptr[cn*(y+anX)];currVal_g=tptr[cn*(y+anX)+1];currVal_r=tptr[cn*(y+anX)+2];
currWRTCenter_b = currVal_b - currValCenter_b;
currWRTCenter_g = currVal_g - currValCenter_g;
currWRTCenter_r = currVal_r - currValCenter_r;
float cur_spw = space_weight[x*ksize.width+y+anX];
#if ABF_GAUSSIAN
weight_b = exp( -0.5f * currWRTCenter_b * currWRTCenter_b/ var_b ) * cur_spw;
weight_g = exp( -0.5f * currWRTCenter_g * currWRTCenter_g/ var_g ) * cur_spw;
weight_r = exp( -0.5f * currWRTCenter_r * currWRTCenter_r/ var_r ) * cur_spw;
#else
weight_b = var_b / ( var_b + (currWRTCenter_b * currWRTCenter_b) ) * cur_spw;
weight_g = var_g / ( var_g + (currWRTCenter_g * currWRTCenter_g) ) * cur_spw;
weight_r = var_r / ( var_r + (currWRTCenter_r * currWRTCenter_r) ) * cur_spw;
#endif
#endif
tmpSum_b += ((float)tptr[cn*(y+anX)] * weight_b);
tmpSum_g += ((float)tptr[cn*(y+anX)+1] * weight_g);
tmpSum_r += ((float)tptr[cn*(y+anX)+2] * weight_r);
totalWeight_b += weight_b, totalWeight_g += weight_g, totalWeight_r += weight_r;
}
}
tmpSum_b /= totalWeight_b;
tmpSum_g /= totalWeight_g;
tmpSum_r /= totalWeight_r;
dest->at(startY,j )= static_cast(tmpSum_b);
dest->at(startY,j+1)= static_cast(tmpSum_g);
dest->at(startY,j+2)= static_cast(tmpSum_r);
}
}
}
}
这里还需要说明的是自适应双边滤波adaptiveBilateralFilter要比双边滤波bilareralFilter运行时间更长,而且从源码来看,明显感觉到两个函数不是一个人写的。更重要的是adaptiveBilateralFilter有bug,当滤波内核尺寸取得更大一些的话,比如Size(10,10),会出现“The application has requested the Runtime toterminate in an unusual way,……”的错误对话框。