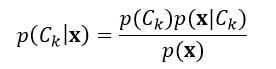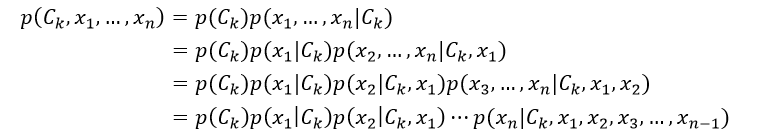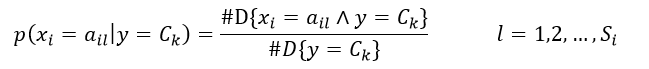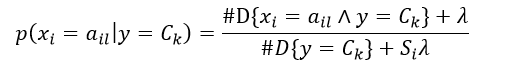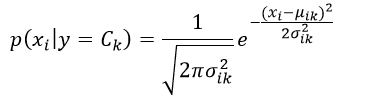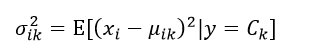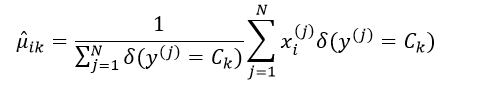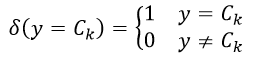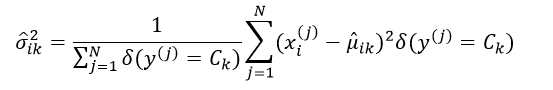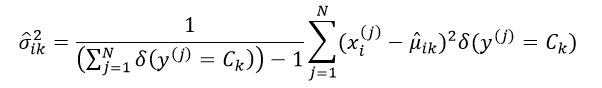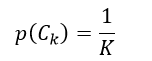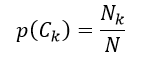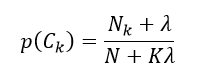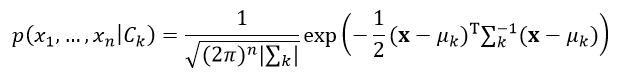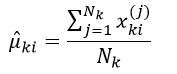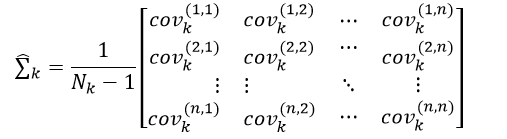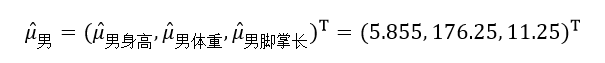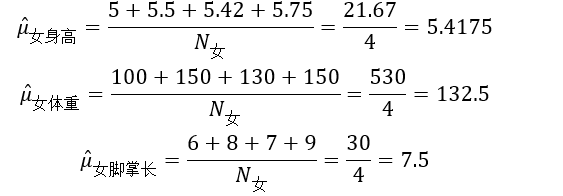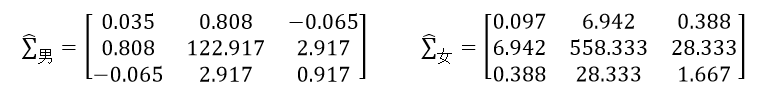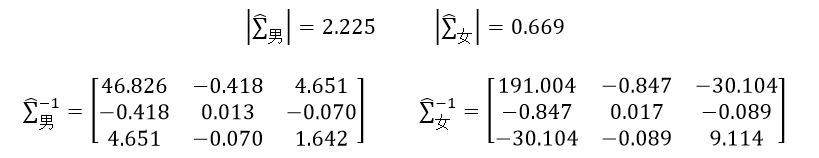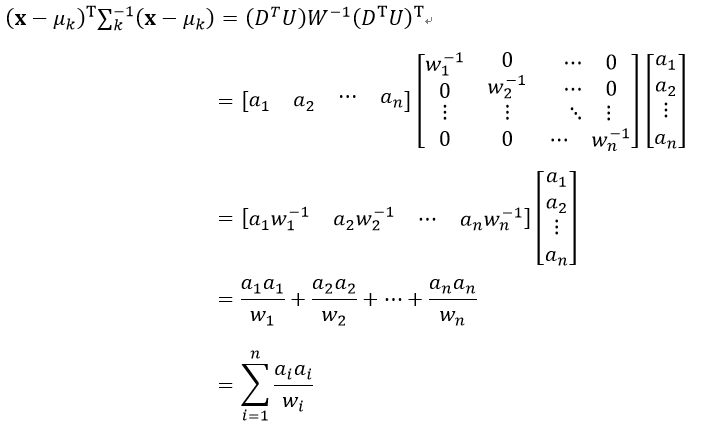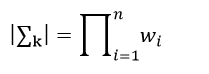Opencv2.4.9源码分析——Normal Bayes Classifier

一、原理

 

OpenCV实现的贝叶斯分类器不是我们所熟悉的朴素贝叶斯分类器（Naïve Bayes Classifier），而是正态贝叶斯分类器（Normal Bayes Classifier），两者虽然英文名称很相似，但它们是不同的贝叶斯分类器。前者在使用上有一个限制条件，那就是变量的特征之间要相互独立，而后者没有这个苛刻的条件，因此它的适用范围更广。为了保持理论的系统性和完整性，我们还是先介绍朴素贝叶斯分类器，然后再介绍正态贝叶斯分类器。

1、朴素贝叶斯分类器

朴素贝叶斯分类器是一种基于贝叶斯理论的简单的概率分类器，而朴素的含义是指输入变量的特征属性之间具有很强的独立性。尽管这种朴素的设计和假设过于简单，但朴素贝叶斯分类器在许多复杂的实际情况下具有很好的表现，并且在综合性能上，该分类器要优于提升树（boosted trees）和随机森林（random forests）。

在许多实际应用中，对于朴素贝叶斯模型的参数估计往往使用的是极大似然法，因此我们可以这么认为，在不接受贝叶斯概率或不使用任何贝叶斯方法的前提下，我们仍然可以应用朴素贝叶斯模型对事物进行分类。

朴素贝叶斯分类器特别适用于输入变量的维数很高的情况，并且它只需要极少量的训练数据就可以估计出分类所需的参数。

抽象地说，朴素贝叶斯是一种条件概率模型：我们要对一个个体进行分类，该个体用代表n个特征（相互独立的变量）的n维向量表示，即x = (x₁,…,x_n)^T，则分配给该个体的概率为：

（1）

该式表示K个可能输出或分类中第k个分类的概率，C_k表示第k个响应输出，即分类结果。

如果个体的特征数量n很大，或者某个特征有大量的数值，则应用式1对个体进行分类是不可行。因此我们应用贝叶斯理论，把条件概率进行分解，使其更利于操作：

（2）

基于认识论的解释，概率是一种置信程度的度量。贝叶斯理论把某个事件在考虑证据之前和之后的置信程度关联了起来。回到式2，p(C_k)表示在不考虑个体x的情况下，第k个分类的概率，我们把它定义为先验概率，而p(C_k|x)表示在考虑个体x的情况下，第k个分类的概率，我们把它定义为后验概率，p(x| C_k)定义为似然度，p(x)定义为标准化常量。

在实际应用中，我们仅仅关心的是式2分式中的分子部分，这是因为分母部分不依赖于分类结果C，并且个体的特征属性F_i是给定的，所以分母是一个常数。

我们再来看式2中的分子部分，它是联合概率模型p(C_k, x₁,…,x_n)。基于链式法则，并重复应用条件概率的定义，这个联合概率模型可以重写为：

（3）

由于是“朴素”的贝叶斯，对于分类C_k来说，特征F_i是有条件的独立于特征F_j的，i≠j。因此，这意味着p(x_i|C_k,x_j) = p(x_i|C_k)，p(x_i|C_k,x_j,x_q) = p(x_i|C_k)，p(x_i|C_k,x_j,x_q,x_l)= p(x_i|C_k)，以此类推，其中i≠j,q, l。则式2又可重写为：

（4）

到目前为止我们得到了特征相互独立的朴素贝叶斯概率模型，我们利用该模型就可以得到具备决策规则的朴素贝叶斯分类器。应用得最普遍的决策规则是最大后验概率（MAP），即选择最可能的假设。则贝叶斯分类器所指定的分类结果为：

（5）

训练朴素贝叶斯分类器的任务是估计两组参数：先验概率p(C_k)和条件概率p(x_i| C_k)。

我们先来计算条件概率p(x_i | C_k)，它分为两种情况：一种是样本数据都是离散的形式，即样本的特征是离散的形式；另一种是样本数据都是连续的数值形式，即样本的特征是数值的形式。

当样本的特征是离散的形式时，条件概率p(x_i | C_k)的估计为

（6）

式中，a_il表示第i个特征可能取的第l个值，S_i表示第i个特征可能选取的所有值的数量，#D{X}表示在由N个训练样本构成的集合D中，满足条件X的样本的数量，因此分式中分母的含义是响应值为C_k的样本数，分子的含义是样本具有a_il值并且响应值为C_k的数量。

式6给出了特征值为a_il并且响应值为C_k的条件概率估计，该方法称为极大似然估计。但该方法可能会出现所要估计的概率值为0的情况，这时会影响到后验概率的计算结果，使分类产生偏差。采用平滑估计可以解决这个问题，即增加一个平滑系数λ，则条件概率为：

（7）

式中，λ≥ 0，显然λ = 0为极大似然估计，当λ = 1时，该平滑方法又称为拉普拉斯平滑。

当样本的特征是数值的形式时，条件概率的分布可以被认为是高斯分布，多项式分布或伯努利分布，则它们的朴素贝叶斯分别被称为高斯朴素贝叶斯，多项式朴素贝叶斯和伯努利朴素贝叶斯。在这里我们只介绍高斯朴素贝叶斯方法

高斯朴素贝叶斯方法是假设对每一个可能的响应值C_k，特征x_i是满足高斯正态分布的，即

（8）

因此我们必须估计出该高斯分布的均值μ_ik和方差σ_ik²：

（9）

（10）

这里一共有2nK个参数，这些参数都需要独立的去估计。估计的方法仍然可以采用极大似然估计。均值μ_ik的极大似然估计为：

（11）

式中上标j表示全部N个训练样本中的第j个样本，函数δ(y = C_k)表示：

（12）

函数δ的作用就是选择那些响应值为C_k的训练样本。

方差σ_ik²的极大似然估计为：

（13）

采用极大似然估计得到的方差是有偏估计，因此往往采用最小方差无偏估计（MVUE）来取代极大似然估计，则此时的σ_ik²估计为：

（14）

我们再来讨论先验概率。贝叶斯分类器只能处理分类问题，即分类结果C具有离散的K个值，因此先验概率p(C_k)的估计相对较简单。当我们已知所有的分类结果出现的概率都是相等的话（如投骰子），则先验概率p(C_k)为

（15）

当我们仅考虑训练样本数据时，则先验概率p(C_k)为

（16）

式中，N表示训练样本的数量，N_k表示分类结果为C_k的训练样本数量。式16这种极大似然估计仍然会有所要估计的概率值为0的情况，因此类似于式7改用平滑估计，得到先验概率为：

（17）

如果我们应用高斯朴素贝叶斯分类器来预测样本，则先根据训练样本计算各个分类的先验概率，以及均值和方差，这样就得到了不同分类下的不同特征属性的高斯函数（式8），然后我们把预测样本数据带入这些不同的高斯函数中，得到不同分类的各个特征属性的似然度，最后把同一分类的先验概率和不同特征的似然度相乘（式5），哪个值大，该预测样本就属于该乘积所对应的分类。

2、正态贝叶斯分类器

下面我们来介绍正态贝叶斯分类器，该分类器只能处理特征值是连续数值的分类问题。

正态贝叶斯分类器认为每一个分类的所有特征属性（即特征向量）服从多变量正态高斯分布，即

（18）

式中，μ_k表示第k个分类所对应的n维均值向量，|∑_k|表示第k个分类所对应的n×n的协方差矩阵∑_k的行列式的值。

因此该分类器认为特征属性之间不必是独立的，这要比朴素贝叶斯的适用条件要宽。则最终包括所有分类的整个分布函数是一个混合高斯分布，而每一个分类就是一个组件（component）。

由贝叶斯规则（式2）可知，后验概率正比于先验概率与似然度的乘积，但在有些情况下可以不考虑先验概率，如分类很少或维数较高等情况，即后验概率仅与似然度成正比，这样最大后验问题就变为了极大似然问题，这时我们只需要得到各个分类的似然度函数（式18），带入新的预测样本，哪个值大，该样本就属于该似然度函数对应的分类，即：

（19）

有时为了计算方法，我们可以把式18取对数，成为对数似然度函数，即

（20）

显然，求式20极大值问题可以转换为求式20中方括号内的极小值问题，其中最后一项nln(2π)是常数，可以不用计算。

为了计算式20，我们需要估计两组参数：均值向量μ_k和协方差矩阵∑_k。

均值向量μ_k的第i个元素（即第i个特征）μ_ki的极大似然估计为：

（21）

式中，x_ki^(j)表示训练样本中属于分类k的第j个样本的第i个特征属性的值，则最终组成的n维（共有n个特征属性）均值向量μ_k的极大似然估计为：

（22）

n×n的协方差矩阵∑_k的无偏估计形式为：

（23）

其中，第p行第q列元素cov_k^(p,q)表示训练样本中第k个分类所组成的数据集合中，第p个特征与第q个特征的协方差，如果p等于q，则为方差，cov_k^(p,q)为：

（24）

我们总结一下正态贝叶斯分类器的执行步骤。首先由训练样本数据估计每个分类的协方差矩阵（式23）和均值向量（式22），然后把这两组变量带入式20中，从而得到了每个分类的完整的对数似然函数。当需要预测样本时，把样本的特征属性值分别带入全部分类的对数似然函数中，最大对数似然函数对应的分类就是该样本的分类结果。

下面举一个例子，该例子是维基百科中英文条目Naive Bayes classifier所列举的例子。

下表是某国人体特征指标的一组统计资料：

序号	性别	身高（英尺）	体重（磅）	脚掌长（英寸）
1	男	6	180	12
2	男	5.92	190	11
3	男	5.58	170	12
4	男	5.92	165	10
5	女	5	100	6
6	女	5.5	150	8
7	女	5.42	130	7
8	女	5.75	150	9

表中的样本一共有8个，分为男和女两类，各有样本数4个，即N_男=4，N_女=4。

由式21先计算男人的均值向量μ_男：

则：

再计算女人的均值向量μ_女：

则：

然后由式23和式24计算男人和女人的协方差矩阵，它们都是3×3的对称方阵。这里我们仅以男人的身高和体重为例，计算它们的协方差cov_男^{(身高，体重)}：

则最终的男人和女人的协方差矩阵分别为：

把得到的男人和女人的均值向量和协方差矩阵带入式20中，就得到两个分类的对数似然函数，由于该函数需要的是协方差矩阵的逆矩阵和行列式的值，所以还需要计算这两组值：

则对数似然函数为：

已知某人身高6英尺，体重130磅，脚掌长8英寸，我们利用前面的训练样本来预测该人是男还是女。预测样本向量x=(6, 130, 8)^T，带入ln(L_男)和ln(L_女)，则分别为-16.314和-28.730，显然ln(L_男)大于ln(L_女)，所以这个人可能是男人。

这里要说明的是维基百科中应用的是高斯朴素贝叶斯分类器，即前面第一部分介绍的内容，它得到的结论是该人为女人。从中我们可以看出，高斯朴素贝叶斯分类器与正态贝叶斯分类器是不同的，正态贝叶斯分类器不在乎特征属性之间是否相互独立，个人认为正态贝叶斯分类器应该更准确一些。

在实际计算似然度函数时，应用奇异值分解会使程序更简洁。由于协方差矩阵∑_k是对称矩阵，所以它的奇异值分解为

（25）

式中，W是由特征值组成的对角线矩阵，U是由特征向量组成的正交矩阵，具有U^-1=U^T的性质，则∑_k的逆矩阵为

（26）

设D= x - μ_k，则(x - μ_k)^T∑_k^-1(x-μ_k)为

（27）

式中，D^T是行向量，U是方阵，则D^TU为行向量，设该行向量的元素为a_i，(D^TU)^T则为列向量，因为W是对角线矩阵，设该矩阵对角线上的元素为w_i，由矩阵的知识可知，W^-1也是对角线矩阵，并且其对角线上的元素为1/w_i，则式27改写为

（28）

我们还注意到一个性质，那就是行列式的值等于该矩阵特征值的乘积，在前面我们已经得到了∑_k的特征值为w_i，则它的行列式值为：

（29）

 

二、源码分析

 

下面我们就详细分析OpenCV中的贝叶斯分类器的源码。再次强调的是OpenCV实现的是正态贝叶斯分类器，不是朴素贝叶斯分类器。

 

CvNormalBayesClassifier类的缺省构造函数：

CvNormalBayesClassifier::CvNormalBayesClassifier()
{
    var_count = var_all = 0;
    var_idx = 0;
    cls_labels = 0;
    count = 0;
    sum = 0;
    productsum = 0;
    avg = 0;
    inv_eigen_values = 0;
    cov_rotate_mats = 0;
    c = 0;
    default_model_name = "my_nb";
}

构建正态贝叶斯分类器的函数：

bool CvNormalBayesClassifier::train( const CvMat* _train_data, const CvMat* _responses,
                            const CvMat* _var_idx, const CvMat* _sample_idx, bool update )
{
    const float min_variation = FLT_EPSILON;    //定义一个很小的数
    bool result = false;    //函数返回的标识变量
    CvMat* responses = 0;    //表示分类结果，即响应值
    const float** train_data = 0;    //表示训练样本数据
    CvMat* __cls_labels = 0;    //表示样本响应值的标签
    CvMat* __var_idx = 0;    //表示特征属性的索引
    CvMat* cov = 0;    //表示某个分类的协方差矩阵

    CV_FUNCNAME( "CvNormalBayesClassifier::train" );

    __BEGIN__;

    int cls, nsamples = 0, _var_count = 0, _var_all = 0, nclasses = 0;
    int s, c1, c2;
    const int* responses_data;    //指向响应值
    //调用cvPrepareTrainData函数，首先判断输入参数_train_data和_responses是否正确，然后由参数_var_idx和_sample_idx得到真正要训练的样本数据train_data，由参数_sample_idx得到所对应的响应值responses，nsamples为得到的train_data中的样本数量，_var_count为train_data中样本特征的数量，_var_all为_train_data中每个样本应该有的特征的数量，__cls_labels为响应值的分类标签的映射矩阵，__var_idx为由参数_var_idx从_var_all中提取的每个样本的特征的掩码矩阵
    CV_CALL( cvPrepareTrainData( 0,
        _train_data, CV_ROW_SAMPLE, _responses, CV_VAR_CATEGORICAL,
        _var_idx, _sample_idx, false, &train_data,
        &nsamples, &_var_count, &_var_all, &responses,
        &__cls_labels, &__var_idx ));

    if( !update )    //不更新数据，即由样本数据重新建立贝叶斯分类器
    {
        const size_t mat_size = sizeof(CvMat*);
        size_t data_size;

        clear();

        var_idx = __var_idx;    //样本特征的掩码矩阵
        cls_labels = __cls_labels;    //响应值的分类标签矩阵
        __var_idx = __cls_labels = 0;    //清零
        var_count = _var_count;    //真正的训练样本所用到的特征数量
        var_all = _var_all;    //全部样本的特征数量

        nclasses = cls_labels->cols;    //表示分类的数量，即K
        data_size = nclasses*6*mat_size;    //定义所需的全部数据的内存空间大小

        CV_CALL( count = (CvMat**)cvAlloc( data_size ));    //分配空间
        memset( count, 0, data_size );    //清零
        //定义不同的空间
        //count表示每个分类的样本数量，即变量Nk
        //sum表示分类中的每种特征属性值的和，即式21的分子部分
        sum             = count      + nclasses; 
        //productsum表示式24中第一个∑
        productsum      = sum        + nclasses;    
        //avg表示均值向量，即式21
        avg             = productsum + nclasses; 
        //inv_eigen_values表示每个分类的协方差矩阵∑k的特征值，最终存储的是特征值的倒数，即式28的1/wi
        inv_eigen_values= avg        + nclasses;   
        //cov_rotate_mats表示每个分类的协方差矩阵的特征向量矩阵的转置，即式25的UT
        cov_rotate_mats = inv_eigen_values         + nclasses;    
        //创建矩阵c，用来表示式20中的ln(|∑k|)
        CV_CALL( c = cvCreateMat( 1, nclasses, CV_64FC1 ));
        //遍历所有分类，创建上面6个矩阵，并清零
        for( cls = 0; cls < nclasses; cls++ )
        {
            // count矩阵的大小为K×n
            CV_CALL(count[cls]            = cvCreateMat( 1, var_count, CV_32SC1 ));
            // sum矩阵的大小为K×n
            CV_CALL(sum[cls]              = cvCreateMat( 1, var_count, CV_64FC1 ));
            // productsum矩阵的大小为K×n×n
            CV_CALL(productsum[cls]       = cvCreateMat( var_count, var_count, CV_64FC1 ));
            // avg矩阵的大小为K×n
            CV_CALL(avg[cls]              = cvCreateMat( 1, var_count, CV_64FC1 ));
            // inv_eigen_values矩阵的大小为K×n
            CV_CALL(inv_eigen_values[cls] = cvCreateMat( 1, var_count, CV_64FC1 ));
            // cov_rotate_mats矩阵的大小为K×n×n
            CV_CALL(cov_rotate_mats[cls]  = cvCreateMat( var_count, var_count, CV_64FC1 ));
            CV_CALL(cvZero( count[cls] ));
            CV_CALL(cvZero( sum[cls] ));
            CV_CALL(cvZero( productsum[cls] ));
            CV_CALL(cvZero( avg[cls] ));
            CV_CALL(cvZero( inv_eigen_values[cls] ));
            CV_CALL(cvZero( cov_rotate_mats[cls] ));
        }
    }
    else    //在已有的贝叶斯分类器的基础上，添加新的训练样本
    {
        // check that the new training data has the same dimensionality etc.
        if( _var_count != var_count || _var_all != var_all || !((!_var_idx && !var_idx) ||
            (_var_idx && var_idx && cvNorm(_var_idx,var_idx,CV_C) < DBL_EPSILON)) )
            CV_ERROR( CV_StsBadArg,
            "The new training data is inconsistent with the original training data" );

        if( cls_labels->cols != __cls_labels->cols ||
            cvNorm(cls_labels, __cls_labels, CV_C) > DBL_EPSILON )
            CV_ERROR( CV_StsNotImplemented,
            "In the current implementation the new training data must have absolutely "
            "the same set of class labels as used in the original training data" );

        nclasses = cls_labels->cols;
    }

    responses_data = responses->data.i;    //指向训练样本的响应值矩阵
    //创建cov矩阵，表示协方差矩阵
    CV_CALL( cov = cvCreateMat( _var_count, _var_count, CV_64FC1 ));

    /* process train data (count, sum , productsum) */
    //遍历所有的训练样本，计算式21的分子和分母部分，以及式24中的第一个∑部分
    for( s = 0; s < nsamples; s++ )
    {
        cls = responses_data[s];    //得到该训练样本的响应值，即分类
        //定义三个矩阵count、sum和productsum的指针
        int* count_data = count[cls]->data.i;
        double* sum_data = sum[cls]->data.db;
        double* prod_data = productsum[cls]->data.db;
        const float* train_vec = train_data[s];    //得到该训练样本数据
        //遍历所有特征
        for( c1 = 0; c1 < _var_count; c1++, prod_data += _var_count )
        {
            //得到该训练样本的第c1个特征属性的值，即式21中的xki(j)
            double val1 = train_vec[c1];
            sum_data[c1] += val1;    //计算式21中的分子部分
            count_data[c1]++;    //计算式21的分母部分
            //计算式24中的第一个∑，即∑xkp(j)xkq(j)，该算式组成的矩阵是对称矩阵，所以只需计算该对称矩阵的一半即可，这里的for循环计算的是该矩阵的右上角部分
            for( c2 = c1; c2 < _var_count; c2++ )
                prod_data[c2] += train_vec[c2]*val1;
        }
    }
    cvReleaseMat( &responses );    //释放responses矩阵
    responses = 0;

    /* calculate avg, covariance matrix, c */
    //遍历所有响应值，即分类结果，计算式21和式23，即均值向量和协方差矩阵，以及式20中的ln(|∑k|)
    for( cls = 0; cls < nclasses; cls++ )
    {
        double det = 1;    //表示协方差矩阵∑k的行列式值
        int i, j;
        CvMat* w = inv_eigen_values[cls];    //表示协方差矩阵|∑k|的特征值，即wi
        //定义三个矩阵count、avg和sum的指针
        int* count_data = count[cls]->data.i;
        double* avg_data = avg[cls]->data.db;
        double* sum1 = sum[cls]->data.db;
        // productsum矩阵是对称矩阵，在前面只计算了该矩阵的右上角部分，在这里调用cvCompleteSymm函数，完成最终的对称矩阵，即把右上角数据对称复制到左下角
        cvCompleteSymm( productsum[cls], 0 );    
        //遍历所有特征属性
        for( j = 0; j < _var_count; j++ )
        {
            int n = count_data[j];    //得到当前分类的第j个特征的数量，即Nk
            avg_data[j] = n ? sum1[j] / n : 0.;    //得到均值向量，即式21
        }
        //指针重新指向矩阵的首地址
        count_data = count[cls]->data.i;
        avg_data = avg[cls]->data.db;
        sum1 = sum[cls]->data.db;
        //遍历所有特征
        for( i = 0; i < _var_count; i++ )
        {
            double* avg2_data = avg[cls]->data.db;    //指向均值向量
            //该指针指向的变量表示的含义是式24中的∑xkq(j)
            double* sum2 = sum[cls]->data.db; 
            //指向productsum矩阵，即式24中的∑xkp(j)xkq(j)
            double* prod_data = productsum[cls]->data.db + i*_var_count;
            double* cov_data = cov->data.db + i*_var_count;    //指向协方差矩阵
            double s1val = sum1[i];    //表示式24中的∑xkp(j)
            double avg1 = avg_data[i];    //表示式24中的μkp的估计
            int _count = count_data[i];    //当前分类的第i个特征的数量，即式24中的Nk
            //遍历前i个特征，即只计算了协方差矩阵（式23）的左下角部分
            for( j = 0; j <= i; j++ )
            {
                double avg2 = avg2_data[j];    //表示式24中的μkq的估计
                //式24
                double cov_val = prod_data[j] - avg1 * sum2[j] - avg2 * s1val + avg1 * avg2 * _count;
                //得到协方差，即式23中的元素
                cov_val = (_count > 1) ? cov_val / (_count - 1) : cov_val;
                cov_data[j] = cov_val;    //协方差赋值
            }
        }
        //协方差矩阵是对称矩阵，在前面只得到了该矩阵cov的左下角部分，这里调用cvCompleteSymm函数，完成最终的对称矩阵，即把左下角数据对称复制到右上角
        CV_CALL( cvCompleteSymm( cov, 1 ));
        //调用cvSVD函数，进行奇异值分解：A=UWVT，这里的cov是A，w是W，cov_rotate_mats[cls]是U的转置（因为CV_SVD_U_T），即式25的UT
        CV_CALL( cvSVD( cov, w, cov_rotate_mats[cls], 0, CV_SVD_U_T ));
        //特征值向量w与常数min_variation比较，选取大值，该代码的作用是去掉那些太小的特征值
        CV_CALL( cvMaxS( w, min_variation, w ));
        //特征值相乘，作用是得到该分类的协方差矩阵的行列式的值，即式29
        for( j = 0; j < _var_count; j++ )
            det *= w->data.db[j];
        //调用cvDiv函数，计算w=1/w，得到特征值的倒数，即式28的1/wi
        CV_CALL( cvDiv( NULL, w, w ));
        //计算式20中的ln(|∑k|)
        c->data.db[cls] = det > 0 ? log(det) : -700;
    }

    result = true;    //标识变量

    __END__;

    if( !result || cvGetErrStatus() < 0 )
        clear();
    //释放内存空间
    cvReleaseMat( &cov );
    cvReleaseMat( &__cls_labels );
    cvReleaseMat( &__var_idx );
    cvFree( &train_data );

    return result;    //返回
}

正态贝叶斯分类器的预测函数predict可以对一个样本进行预测，也可以同时对多个样本进行预测，但预测样本不能缺失任何一个特征属性。当只预测一个样本时，该函数的返回值就是预测分类结果。当预测多个样本是，样本以行的形式存储在参数矩阵samples中，而返回的预测结果存储在参数向量results中，因此这种情况results必须被定义。

float CvNormalBayesClassifier::predict( const CvMat* samples, CvMat* results ) const
{
    float value = 0;    //单一预测样本的返回值
    //判断输入参数矩阵samples的正确性
    if( !CV_IS_MAT(samples) || CV_MAT_TYPE(samples->type) != CV_32FC1 || samples->cols != var_all )
        CV_Error( CV_StsBadArg,
        "The input samples must be 32f matrix with the number of columns = var_all" );
    //如果是预测多个样本，输入参数results必须被定义
    if( samples->rows > 1 && !results )
        CV_Error( CV_StsNullPtr,
        "When the number of input samples is >1, the output vector of results must be passed" );
    //判断输入参数results的正确性，该向量的元素数量必须等于预测的样本数
    if( results )
    {
        if( !CV_IS_MAT(results) || (CV_MAT_TYPE(results->type) != CV_32FC1 &&
        CV_MAT_TYPE(results->type) != CV_32SC1) ||
        (results->cols != 1 && results->rows != 1) ||
        results->cols + results->rows - 1 != samples->rows )
        CV_Error( CV_StsBadArg, "The output array must be integer or floating-point vector "
        "with the number of elements = number of rows in the input matrix" );
    }
    //表示训练样本中全部特征属性中的真正用到的特征，在这里vidx为0
    const int* vidx = var_idx ? var_idx->data.i : 0; 
    //调用predict_body函数，并行处理各个预测样本，该语句需要TBB库支持
    cv::parallel_for_(cv::Range(0, samples->rows),
                      predict_body(c, cov_rotate_mats, inv_eigen_values, avg, samples,
                                   vidx, cls_labels, results, &value, var_count));

    return value;
}

预测样本的主体结构：

struct predict_body : cv::ParallelLoopBody {
  predict_body(CvMat* _c, CvMat** _cov_rotate_mats, CvMat** _inv_eigen_values, CvMat** _avg,
     const CvMat* _samples, const int* _vidx, CvMat* _cls_labels,
     CvMat* _results, float* _value, int _var_count1
  )
  {
    c = _c;    //表示各个分类的式20中的ln(|∑k|)
    cov_rotate_mats = _cov_rotate_mats;    //表示式25中的UT
    inv_eigen_values = _inv_eigen_values;    //表示式28中的1/wi
    avg = _avg;    //表示各个分类的均值向量的估计
    samples = _samples;    //表示预测样本数据
    vidx = _vidx;    //表示特征属性
    cls_labels = _cls_labels;    //表示样本的分类标签
    results = _results;    //表示预测多个样本的分类结果
    value = _value;    //表示预测单个样本的分类结果
    var_count1 = _var_count1;    //表示特征属性的数量
  }

  CvMat* c;
  CvMat** cov_rotate_mats;
  CvMat** inv_eigen_values;
  CvMat** avg;
  const CvMat* samples;
  const int* vidx;
  CvMat* cls_labels;

  CvMat* results;
  float* value;
  int var_count1;
  //重载()运算符
  void operator()( const cv::Range& range ) const
  {

    int cls = -1;
    int rtype = 0, rstep = 0;
    int nclasses = cls_labels->cols;    //分类的数量，即响应值的数量
    int _var_count = avg[0]->cols;    //特征属性的数量

    if (results)
    {
        rtype = CV_MAT_TYPE(results->type);    //数据类型
        //步长
        rstep = CV_IS_MAT_CONT(results->type) ? 1 : results->step/CV_ELEM_SIZE(rtype);
    }
    // allocate memory and initializing headers for calculating
    cv::AutoBuffer buffer(nclasses + var_count1);    //开辟一块内存空间
    //定义矩阵diff，前期代表x-μk，即式27中的D，后期代表式27中DTU
    CvMat diff = cvMat( 1, var_count1, CV_64FC1, &buffer[0] );
    //遍历samples矩阵的所有行，即遍历所有预测样本数据
    for(int k = range.start; k < range.end; k += 1 )
    {
        int ival;
        double opt = FLT_MAX;    //定义一个很大的数
        //遍历所有的响应值
        for(int i = 0; i < nclasses; i++ )
        {

            double cur = c->data.db[i];    //得到当前分类的ln(|∑k|)
            CvMat* u = cov_rotate_mats[i];    //得到当前分类的协方差矩阵的特征向量矩阵的转置，即式25中的UT
            CvMat* w = inv_eigen_values[i];    //得到当前分类的协方差矩阵的特征值的倒数，即式28中的1/wi

            const double* avg_data = avg[i]->data.db;    //指向当前分类的均值向量
            //得到第k个预测样本数据
            const float* x = (const float*)(samples->data.ptr + samples->step*k);

            // cov = u w u'  -->  cov^(-1) = u w^(-1) u'
            //遍历所有特征，计算式27中的D=x-μk，这里虽然是μk -x，但并不影响最终的结果
            for(int j = 0; j < _var_count; j++ )
                diff.data.db[j] = avg_data[j] - x[vidx ? vidx[j] : j];
            //调用cvGEMM函数，执行矩阵相乘，即diff = diff*uT，由于这里的变量u是式25的UT，因此两次转置后又是原值U，之所以要进行两次转置，是为了加快运行速度。最终diff为DTU，即[a1,a2,…,an]
            cvGEMM( &diff, u, 1, 0, 0, &diff, CV_GEMM_B_T );
            //遍历特征属性，计算ln(|∑k |) + (x - μk)T∑k-1(x - μk)，即式20方括号内除nln(2π)的部分
            for(int j = 0; j < _var_count; j++ )
            {
                double d = diff.data.db[j];    //得到DTU
                // d*d*w为式28，另外cur的初始值为ln(|∑k |)
                cur += d*d*w->data.db[j];
            }
            //得到不同分类的最小值
            if( cur < opt )
            {
                cls = i;    //最小值对应的分类
                opt = cur;    //更新最小值
            }
            /* probability = exp( -0.5 * cur ) */
        }

        ival = cls_labels->data.i[cls];    //预测结果的分类标签对应的响应值
        //如果是预测多个样本，则把预测结果放入results向量的相应位置上
        if( results ) 
        {
            if( rtype == CV_32SC1 )
                results->data.i[k*rstep] = ival;
            else
                results->data.fl[k*rstep] = (float)ival;
        }
        //如果是预测一个样本，则赋值该预测结果
        if( k == 0 )
            *value = (float)ival;
    }
  }
};

三、应用实例

 

我们还是以前面预测男人和女人为例，应用程序实现预测：

#include "opencv2/core/core.hpp"
#include "opencv2/highgui/highgui.hpp"
#include "opencv2/imgproc/imgproc.hpp"
#include "opencv2/ml/ml.hpp"

#include 
using namespace cv;
using namespace std;

int main( int argc, char** argv )
{	
	float trainingData[8][3] = { {6, 180, 12}, {5.92, 190, 11}, {5.58, 170, 12}, {5.92, 165, 10},
								{5, 100, 6}, {5.5, 150, 8},{5.42, 130, 7}, {5.75, 150, 9}};
	Mat trainingDataMat(8, 3, CV_32FC1, trainingData); 

	float responses[8] = {'M', 'M', 'M', 'M', 'F', 'F', 'F', 'F'};
	Mat responsesMat(8, 1, CV_32FC1, responses);

	CvNormalBayesClassifier nbc;
	nbc.train(trainingDataMat, responsesMat); 

	float myData[3] = {6, 130, 8};
	Mat myDataMat(1, 3, CV_32FC1, myData);
	float r = nbc.predict( myDataMat );

	cout<

得到的结果为：

result: M

与我们前面的计算结果一致。