两种图像骨架提取算法的研究(1)原理部分

图像骨架提取，实际上就是提取目标在图像上的中心像素轮廓。说白了就是以目标中心为准，对目标进行细化，

一般细化后的目标都是单层像素宽度。比如输入图像是这样：

输出骨架图像(红色)

关于骨架提取，现存的算法有一千种以上（论文[1]中谈到，There are more than one thousand algorithms thathave been published on this topic）。论文[1]中提到，所有的骨架提取算法无外乎分为迭代和非迭代两大类。在迭代算法中，又分为并行迭代和顺序迭代两种。

本文分别介绍两种提取算法，它们分别来源于论文[1](K3M顺序迭代)、[2](Zhang-Suenalgorithm,并行迭代)。

这两种方法都是对二值图像操作的，思想都是从目标外围往目标中心，利用以待检测像素为中心3*3像素窗口的特征，对目标不断腐蚀细化，直至腐蚀到不能再腐蚀（单层像素宽度），就得到了图像的骨架。下面详细介绍一下两种骨架提取算法。

一  K3M

该算法的思想是，提取目标外围轮廓，然后利用轮廓腐蚀目标图像边界（这是一次迭代过程），

直至腐蚀到不能再腐蚀。

算法分为两块

第一块，不断腐蚀，提取出伪骨架(部分区域有两层像素宽度，但已经很接近真实骨架)。

第二块，从伪骨架中提取真实骨架。

第一块：提取出伪骨架

每次迭代共有6步。不断迭代，直至某次迭代的过程，目标边界中没有新的像素被腐蚀，那么此时，剩余的目标图像像素就很接近于真实骨架(称之为伪骨架)。

<1>提取最新目标轮廓(初始为原目标轮廓)并记录这些轮廓点。

<2>依次检测这些轮廓点的8像素邻域，是否只含有3连通像素，如果有，把此点从轮廓点删除，并在目标图像中删除（腐蚀掉）对应点。

<3>依次检测<2>中剩余轮廓点的8像素邻域，是否只含有3 or 4连通像素，如果有，把此点从轮廓点删除，并在目标图像中删除（腐蚀掉）对应点。

<4>依次检测<3>中剩余轮廓点的8像素邻域，是否只含有3 or 4 or 5连通像素，如果有，把此点从轮廓点删除，并在目标图像中删除（腐蚀掉）对应点。

<5>依次检测<4>中剩余轮廓点的8像素邻域，是否只含有3 or 4 or 5 or 6连通像素，如果有，把此点从轮廓点删除，并在目标图像中删除（腐蚀掉）对应点。

<6>依次检测<5>中剩余轮廓点的8像素邻域，是否只含有3 or 4 or 5 or 6 or 7连通像素，

如果有，把此点从轮廓点删除，并在目标图像中删除（腐蚀掉）对应点。

这是一次迭代过程的最后一步，如果在这步骤中仍有像素被腐蚀，

说明除了真实骨架还有”肉”，仍需继续腐蚀边界。这一步骤是算法迭代的终止条件。

第二块 从伪骨架中提取真实骨架。

算法第一块得到的伪骨架有部分区域是两个像素宽度，而目标骨架是单层像素宽度。所以，通过下面这一步骤提取最终骨架：

依次检测目标图像中，伪骨架的8像素邻域，是否只含有2 or 3 or 4 or 5 or 6 or 7连通像素，如果有，把此点从伪骨架中删除(腐蚀)，就得了最终的骨架。

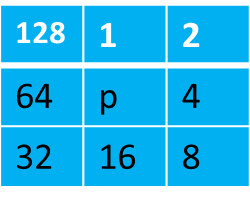
该论文对像素p的8邻域进行了权重编码：对判断像素点p周围8邻域的最大连通区域，是否只含有n（2

比如判断点p的8邻域是否只含有2连通的区域，可以这样实现：

                                                          

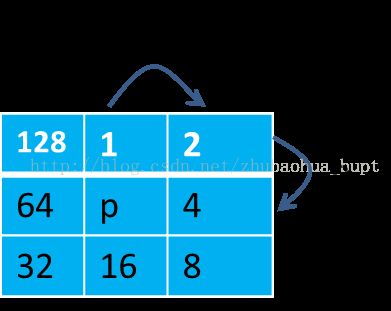
把相邻2连通像素两两相加，会得到一个这样的集合c2{3,6,12,24,48,96,192,129},

由于操作的是二值图像，在判断p的8邻域的最大连通域是否只含有2连通域时，

只需要对p的8邻域进行加权相加得到一个值，记作p2，然后去c2里查询，

如果c2里有p2，则点p周围的8邻域只含有2连通的区域。比如：

         这样的加权方式，使得每个可能出现的n（2

原文中查询集合：

A1=3连通,{}

A2=3or4连通,

A3=3 or 4 or 5连通,

A4=3 or 4 or 5 or 6连通,

A5=3 or 4 or 5 or 6 or 7连通

A0=2 or3 or 4 or 5 or 6 or 7连通

需要注意的是，每次迭代中的每一小步顺序不能变，否则会在腐蚀拐点的时候出现漏网之鱼，随着迭代的次数增加，效果就会和真实的骨架偏差越来越大。

 

二 Zhang-Suen algorithm

这个算法是论文[2]提出的，该算法每一次的迭代步骤是对符合特定条件的目标像素，进行腐蚀，效果就是目标变得越来越细。不断的迭代，直到在上一次腐蚀后的目标在本轮操作中，没有新的像素点被腐蚀，算法结束。

下面说一下此算法的四个条件：

条件(a)：中心像素P1周围的目标像素（二值中的1）的个数之和在2和6之间。

条件(b): 8邻域像素中，按顺时针方向，相邻两个像素出现0->1的次数。

比如，下面这个例子,A(P1)=2。

条件(c)(d)有两种模式，一种上面提到过，下面是另一种。

                        Zhang-Suen thinning steps:

                                     While points are deleted do

                                             For all pixels p(i,j) do

                                                        if   (a)2 ≤ B(P1) ≤ 6
                                                              (b) A(P1) = 1
                                                              (c) Apply oneof the following:
                                                                       1. P2 x P4 x P6 = 0 in odd iterations
                                                                       2. P2 x P4 x P8 = 0 in even iterations
                                                              (d) Apply oneof the following:
                                                                       1. P4 x P6 x P8 = 0 in odd iterations
                                                                        2. P2 x P6 x P8 = 0 in even iterations
                                                        then

                                                              Deletepixel p(i,j)

                                                        endif

                                          end for

                                    end while

参考论文：

[1]:K3M: A UNIVERSAL ALGORITHM FOR IMAGE SKELETONIZATION AND A REVIEW OF THINNING TECHNIQUES

[2]:A fast parallel algorithm for thinning digital patterns

两种算法的代码见下篇博客。