1、过拟合怎么产生的?
模型训练之初,你压根不知道哪些特征会有用,于是你找了很多特征,以此来尽可能精确地去拟合训练数据。
这样的结果往往就是,你用上了一些其实不重要的特征,虽然加上这些特征,会在训练集中表现很好,甚至拿到满分,但是我们的目标并不是让模型在训练集上取得满分,而是在正儿八经的测试集,这种大考中,取得优秀的表现。
十有八九,我们第一次训练出来的模型,会出现过拟合,也就是说,在测试集表现的没有在训练集上好,甚至差不少。
这是为什么?
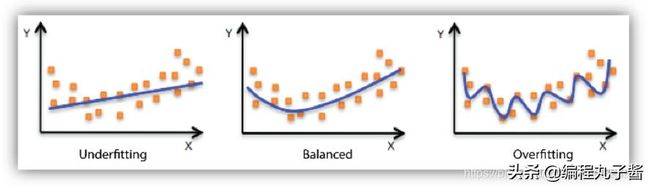
分析发现,我们在模型中使用的某些特征,本身就不具备普适性。但你通过训练集,还是学习到它了,因为你的模型,想法设法地拟合了所有的样本点,自然而然地就会出来很多特征参数,如下图,第三幅图的模型复杂程度远大于第一幅。
图片来源于网络
在这种不具备普遍性的情况下学习到它,自然会影响你测试集的效果,自然就做不出泛化能力强的模型,就产生了过拟合。
当然了,并不是只要参数一多就会过拟合,还要看你的样本量。
2 、消除过拟合的通俗理解
先不用管L1, L2正则到底是干啥的,它们之间有何区别等这样的问题。
按照逻辑,遇到过拟合这个问题,直接解决过拟合就行。
我们不妨先想想,如果想消除几个原来模型中的特征,你会怎么去做?比如我们学到了一个模型:
y = tanh(w1x1 + w2x2 + w3x3 + w4x4)
如果想变弱或消除特征x3, 其实很简单的。直接添加一项 -w3*常数就会达到效果,对吗?yeah, 这样不就变弱特征x3的作用了吗。
其实还是不难理解的。
3 、相比L2,L1正则更可能使模型变稀疏?
关于这个问题的回答,近日,我查阅到了几篇讲的比较好的博客,非常通俗地解释了这个问题。
https://blog.csdn.net/weixin_39750084/article/details/83661413
https://www.zhihu.com/question/37096933
L1就是对模型中每个特征取绝对值,L2取平方。
首先,为解释问题做铺垫。
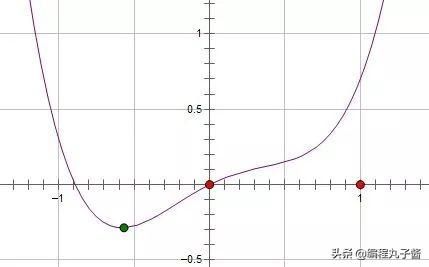
假如,我们的模型Loss函数与某个特征w 的关系如下:
图片来源于网络
如果施加 L1,则新的函数为:Loss()+C|w|,要想消除这个特征的作用,只需要令 w = 0,使它取得极小值即可。
且可以证明:添加L1正则后 ,只要满足:
系数 C 大于原函数在 0 点处的导数的绝对值,
w = 0 就会变成一个极小值点。
证明过程如下,如上图所示,要想在0点处取得极小值,根据高数基本知识:
1) w小于0时,d(Loss)/d(w) - C 小于0
2) 且,w大于0时,d(Loss)/d(w) + C 大于0
上面两个式子同时满足,可以简写为:| d(Loss)/d(w) | < C, 得证。
图片来源于网络
如果施加 L2, 则新的函数为:Loss()+Cw^2 ,求导可得:d(Loss)/d(w) + 2Cw,要想在w = 0点处取得极小值,必须得满足:
d(Loss)/d(w) = 0
言外之意,如果原函数在0点处的导数不为 0,那么施加 L2 正则后导数依然不为 0,也就不会在0点处取得极小值。
这种概率很明显小于L1正则在0点处取得极小值的概率值,由此可得,L1更容易使得原来的特征变弱或消除,换句话说就是更容易变稀疏。
讲完了,读者朋友们,你们看明白了吗?
欢迎在文章下面评论哦!
获取更多编程信息以及学习资料请搜索关注下方公众号!