机器学习&图像分割——模型评价总结(含完整代码)

                                       

                                    机器学习&图像分割——模型评价总结（含完整代码）

---

• 模型评价的方法指标有很多，如：PR-curve，MAE，ROC，Precision，Recall，AUC，AP，mAP，DSI，VOE，RVD等等；
• 本文旨在介绍机器学习&图像分割的模型评价指标，包括完整代码，持续更新中......
• 码字不易，若有帮助，恳请点赞

---

问题1：在显著性检测方面，假设现有三种方法（DSR，GMA，MCA）检测标准数据库中的部分图像（还有原图与真值图），分别得到三种结果，如何求三种方法与真值图之间的MAE（平均绝对误差），并绘制PR-curve曲线图呢？

（1）image原图

（2）mask图像 (ground truth，真值图)

（3）resultsDSR图像

（4）resultsGMA图像

（5）resultsMCA图像

文件夹内容如下图，链接：https://pan.baidu.com/s/1Wg_necXBCYsCk7pf2s7gog 或PR-curve绘制，密码：lka7

输出结果为：

具体实现——Matlab代码如下：

clear all;clc;close all;
addpath('Functions\');%加载文件夹Functions中的函数
%% 三种方法得到的结果路径，以及真值图路径
result1 = 'resultsDSR\';
result2 = 'resultsMCA\';
result3 = 'resultsGMR\';
mask = 'mask\';
%% 创建文件夹evaluation index，目的是保存PR曲线图
newFolder = 'evaluation index'; 
if ~exist(newFolder)
    mkdir(newFolder);
end
%% Evaluation index 1: evaluating MAE
resultSuffixDSR = '_DSR.png';
resultSuffixMCA = '_MCA.png';
resultSuffixGMR = '_stage1.png';
gtSuffix = '.png';

maeDSR = CalMeanMAE(result1, resultSuffixDSR, mask, gtSuffix);
maeMCA = CalMeanMAE(result2, resultSuffixMCA, mask, gtSuffix);
maeGMR = CalMeanMAE(result3, resultSuffixGMR, mask, gtSuffix);
%% Evaluation index 2: ploting PR curve
[rec1, prec1] = DrawPRCurve(result1, resultSuffixDSR, mask, gtSuffix, true, true, 'r');
hold on
[rec2, prec2] = DrawPRCurve(result2, resultSuffixMCA, mask, gtSuffix, true, true, 'g');
hold on
[rec3, prec3] = DrawPRCurve(result3, resultSuffixGMR, mask, gtSuffix, true, true, 'b');
hold off;
grid on;
box on;
xlabel('Recall');
ylabel('Precision');
% title(strcat('PR-curve','  ( ',sprintf(' MAE = %1.6f ',maeDSR),' )'));
title('PR-curve');
lg = legend({'DSR method','CA method','GMR method'});
set(lg, 'location', 'southwest');
k=1.2;
set(gcf,'units',get(gcf,'paperunits'));
set(gcf,'paperposition',get(gcf,'position')*k);
saveas(gcf,strcat(newFolder,'\PR-curve','.bmp'));

 

问题2：医学图像分割领域中的模型评价指标总结

强烈建议参照以下两篇文章：

《Performance measure characterization for evaluating neuroimage segmentation algorithms》

《Metrics for evaluating 3D medical imagesegmentation: analysis, selection, and tool》

度量指标分析工具github:https://github.com/Visceral-Project/EvaluateSegmentation

1、医学图像比赛（ISBI2017或者MICCAI2007）中常用到的几个度量指标：DICE，VOE，RVD，ASD，MSD等等；如何编程实现？（Matlab代码与Python代码）

符号定义：

         ：  代表 ground truth的分割结果

         ：代表预测的分割结果

（1）DICE（值域为[0,1]）: 使用频率最高。数学定义如下，具体表示两个物体相交的面积占总面积的比值，完美分割该值为1。 

（2）VOE（volumetric overlap error）： 与DICE类似，数学定义如下，它将and操作换成了减法操作，以此来代表错误率。

                                                                       

（3）RVD（relative volume difference）：表示两者体积之间的差异，数学定义如下。

（4）ASD（average symmetric surface distance）： 先定义 代表的是预测的中的边界的像素，同样地可以得到的定义。然后对的定义，同理可得的定义。那么ASD的数学定义为： 

（5）MSD（maximum symmetric surface distance）：与ASD定义比较类似，只不过把计算平均的操作替换成了计算最大值的操作。其数学定义为：

参照博客：图像分割评价标准。具体代码见链接：https://pan.baidu.com/s/1C7BWIebYbE4EJIoGKtjLSA，密码是：gjlb，内容如下：

（一）Matlab 具体的代码实现如下：

主函数demo：

clc;clear all;close all;
%% step 1：读入图像  
SEG = imread('0009_CHS.png');      % 读入分割图像
GT  = imread('0009.png');          % 读入真值图像
  
%% step 2：灰度化
if (length(size(SEG))>2 && length(size(GT))>2)
    SEG = im2gray(SEG);            % 灰度化分割图像
    GT  = im2gray(GT);             % 灰度化真值图像
end
    
%% step 3：二值化
SEG = imbinarize(SEG);             % 二值化分割图像
GT  = imbinarize(GT);              % 二值化真值图像

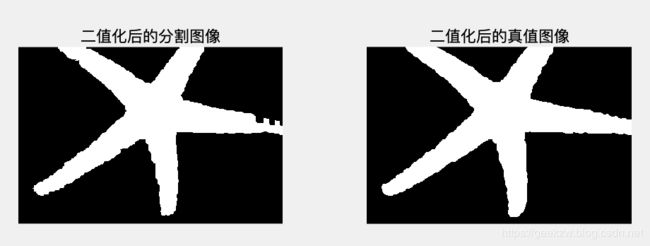
%% step 4：画图预览
figure(1),
subplot(121),imshow(SEG);
title('二值化后的分割图像');
subplot(122),imshow(GT);
title('二值化后的真值图像');

%% step 5：计算各个评价指标

% (1)计算DICE系数
DSI = calDSI(SEG, GT);   
fprintf('(1) DICE系数：        DSI       =  %.4f\n',DSI);

% (2)计算VOE系数
VOE = calVOE(SEG, GT);   
fprintf('(2) VOE系数：         VOE       =  %.4f\n',VOE);

% (3)计算RVD系数
RVD = calRVD(SEG, GT); 
fprintf('(3) RVD系数：         RVD       =  %.4f\n',RVD);

% (4)计算Precision系数
Precision = calPrecision(SEG, GT); 
fprintf('(4) Precision系数：   Precision =  %.4f\n',Precision);

%（5）计算Recall系数
Recall = calRecall(SEG, GT); 
fprintf('(5) Recall系数：      Recall    =  %.4f\n\n\n',Recall);

disp('其他评价指标的计算');
% (6)其他评价指标的计算
jaccard     = Jaccard_Index(SEG, GT)
sensitivity = getSensitivity(SEG, GT)
hd          = Hausdorff_Dist(SEG, GT)
apd         = Avg_PerpenDist(SEG, GT)
confm_index = ConformityCoefficient(SEG, GT)

先看运行结果：

 

 其中调用函数文件分别为：

（a）calDSI函数文件：

function DSI = calDSI(SEG, GT)  
    % SEG, GT are the binary segmentation and ground truth areas, respectively.  
    % 计算DICE系数，即DSI  
    DSI = 2*double(sum(uint8(SEG(:) & GT(:)))) / double(sum(uint8(SEG(:))) + sum(uint8(GT(:))));  
end  

(b) calVOE函数文件：

function VOE = calVOE(SEG, GT)  
    % SEG, GT are the binary segmentation and ground truth areas, respectively.  
    % 计算VOE系数，即VOE  
    VOE = 2*double(sum(uint8(SEG(:))) - sum(uint8(GT(:)))) / double(sum(uint8(SEG(:))) + sum(uint8(GT(:))));  
end  

(c) calRVD函数文件：

function RVD = calRVD(SEG, GT)  
    % SEG, GT are the binary segmentation and ground truth areas, respectively.  
    % 计算RVD系数，即RVD  
    RVD = double(sum(uint8(SEG(:))) ) / double(sum(uint8(GT(:)))) - 1;  
end  

(d) calPrecision函数文件：

function precision = calPrecision(SEG, GT)  
    % SEG, GT are the binary segmentation and ground truth areas, respectively.  
    % precision  
    precision = double(sum(uint8(SEG(:) & GT(:)))) / double(sum(uint8(SEG(:))));  
end  

(e) calRecall函数文件：

function recall = calRecall(SEG, GT)  
    % SEG, GT are the binary segmentation and ground truth areas, respectively.  
    % recall  
    recall = double(sum(uint8(SEG(:) & GT(:)))) / double(sum(uint8(GT(:))));  
end  

 (f) 其他指标的函数文件见以上链接。

（二）Python代码如下：

import cv2
from matplotlib import pyplot as plt


# 计算DICE系数，即DSI
def calDSI(binary_GT,binary_R):
    row, col = binary_GT.shape  # 矩阵的行与列
    DSI_s,DSI_t = 0,0
    for i in range(row):
        for j in range(col):
            if binary_GT[i][j] == 255 and binary_R[i][j] == 255:
                DSI_s += 1
            if binary_GT[i][j] == 255:
                DSI_t += 1
            if binary_R[i][j]  == 255:
                DSI_t += 1
    DSI = 2*DSI_s/DSI_t
    # print(DSI)
    return DSI

# 计算VOE系数，即VOE
def calVOE(binary_GT,binary_R):
    row, col = binary_GT.shape  # 矩阵的行与列
    VOE_s,VOE_t = 0,0
    for i in range(row):
        for j in range(col):
            if binary_GT[i][j] == 255:
                VOE_s += 1
            if binary_R[i][j]  == 255:
                VOE_t += 1
    VOE = 2*(VOE_t - VOE_s)/(VOE_t + VOE_s)
    return VOE

# 计算RVD系数，即RVD
def calRVD(binary_GT,binary_R):
    row, col = binary_GT.shape  # 矩阵的行与列
    RVD_s,RVD_t = 0,0
    for i in range(row):
        for j in range(col):
            if binary_GT[i][j] == 255:
                RVD_s += 1
            if binary_R[i][j]  == 255:
                RVD_t += 1
    RVD = RVD_t/RVD_s - 1
    return RVD

# 计算Prevision系数，即Precison
def calPrecision(binary_GT,binary_R):
    row, col = binary_GT.shape  # 矩阵的行与列
    P_s,P_t = 0,0
    for i in range(row):
        for j in range(col):
            if binary_GT[i][j] == 255 and binary_R[i][j] == 255:
                P_s += 1
            if binary_R[i][j]   == 255:
                P_t += 1

    Precision = P_s/P_t
    return Precision

# 计算Recall系数，即Recall
def calRecall(binary_GT,binary_R):
    row, col = binary_GT.shape  # 矩阵的行与列
    R_s,R_t = 0,0
    for i in range(row):
        for j in range(col):
            if binary_GT[i][j] == 255 and binary_R[i][j] == 255:
                R_s += 1
            if binary_GT[i][j]   == 255:
                R_t += 1

    Recall = R_s/R_t
    return Recall



if __name__ == '__main__':
    # step 1：读入图像，并灰度化
    img_GT = cv2.imread('0009.png',0)
    img_R  = cv2.imread('0009_CHS.png',0)
    # imgray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)   # 灰度化
    # img_GT = img_GT[:,:,[2, 1, 0]]
    # img_R  = img_R[:,: [2, 1, 0]]

    # step2：二值化
    # 利用大律法,全局自适应阈值 参数0可改为任意数字但不起作用
    ret_GT, binary_GT = cv2.threshold(img_GT, 0, 255, cv2.THRESH_BINARY | cv2.THRESH_OTSU)
    ret_R, binary_R   = cv2.threshold(img_R, 0, 255, cv2.THRESH_BINARY | cv2.THRESH_OTSU)

    # step 3： 显示二值化后的分割图像与真值图像
    plt.figure()
    plt.subplot(121),plt.imshow(binary_GT),plt.title('真值图')
    plt.axis('off')
    plt.subplot(122),plt.imshow(binary_R),plt.title('分割图')
    plt.axis('off')
    plt.show()


    # step 4：计算DSI
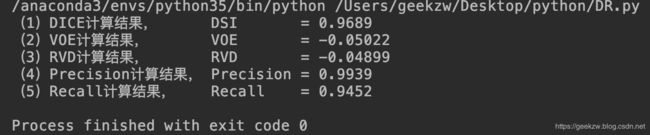
    print('（1）DICE计算结果，      DSI       = {0:.4}'.format(calDSI(binary_GT,binary_R)))  # 保留四位有效数字

    # step 5：计算VOE
    print('（2）VOE计算结果，       VOE       = {0:.4}'.format(calVOE(binary_GT,binary_R)))

    # step 6：计算RVD
    print('（3）RVD计算结果，       RVD       = {0:.4}'.format(calRVD(binary_GT,binary_R)))

    # step 7：计算Precision
    print('（4）Precision计算结果， Precision = {0:.4}'.format(calPrecision(binary_GT,binary_R)))

    # step 8：计算Recall
    print('（5）Recall计算结果，    Recall    = {0:.4}'.format(calRecall(binary_GT,binary_R)))

运行结果：

 

2、分割精度、过分割率、欠分割率的定义

（1）分割精度：分割准确的面积占GT图像中真实面积的百分比，数学定义如下：

      其中表示专家手工勾画出的分割图像的参考面积，表示算法分割得到的图像的真实面积，表示错误分割的像素点个数。

（2）过分割率：即分割在GT图像参考面积之外的像素点的比率，数学定义如下：

        其中表示本不应该包含在分割结果中的像素点个数，实际却在分割结果中的像素点个数。换句话讲，中的像素点出现在实际分割图像中，但不出现在理论分割图像中。

（3）欠分割率：即分割在GT图像参考面积之中欠缺的像素点的比率，数学定义如下：

       其中表示本应该包含在分割结果中的像素点个数，实际却不在分割结果中的像素点个数。换句话讲，中的像素点出现在理论分割图像中，但不出现在实际分割图像中。

 

3、灵敏度与特异度的定义

假设实验图像为I，真实分割结果为G，实际分割结果为R。

（1）灵敏度：将实际是感兴趣区域的像素点正确地判断为感兴趣区域像素的比例，其衡量的是分割实验中能分割感兴趣区域的能力，其数学定义如下。

（1）特异度：将实际不是感兴趣区域的像素点正确地判断为不是感兴趣区域像素的比例，其衡量的是分割实验中能正确判断不是感兴趣区域像素点的能力，其数学定义如下。

Matlab的灵敏度函数：

function sen = getSensitivity(SEG, GT)  
    % SEG, GT are the binary segmentation and ground truth areas, respectively.  
    % sensitivity  
    sen = double(sum(uint8(SEG(:) & GT(:)))) / double(sum(uint8(SEG(:))));  
end  

 

参考网址：

1、如何在CSDN博客插入公式：http://private.codecogs.com/latex/eqneditor.php

2、图像分割结果评价：https://blog.csdn.net/zhuason/article/details/52989091

3、图像分割评价标准代码：https://blog.csdn.net/yangyangyang20092010/article/details/51637073