一种基于支配和分解的多目标优化进化算法学习笔记
Algorithm Based on Dominance and Decomposition》作者是Ke Li, Student Member, IEEE, Kalyanmoy Deb, Fellow, IEEE, Qingfu Zhang, Senior Member, IEEE, and Sam Kwong, Fellow, IEEE，作为一个对多目标优化问题从来没接触过的人，这可着实花了我不少时间来琢磨，下面我就讲讲在这篇论文中的我所理解的算法。
名词解释：
- EF:理论上的pareto最优向量集
- EMO:进化多目标优化
- EA：进化算法
- MOEA:多目标进化算法
- MOEA/D:基于分解的多目标进化算法
- MOEA/DD:基于支配和分解的多目标优化进化算法
- NSGA-II:非支配排序遗传算法
多目标优化：
首先，多目标优化的概念就是好比说：你想买车，但是呢，你又想买的车价格低，又想油耗低，安全性高，但是我们都知道这个常识，汽车的价格越低，各个性能就差，此时的价格低，油耗低，安全性高就组成了一个具有相互冲突的目标函数。多目标优化问题（MOP）可以描述为：
- J、K：不等式和等式约束条件的个数
- 决策空间：
即可行域，满足gj(x)和hk(x)约束的一块x区域,可看做定义域 - 目标空间：
- m个相互冲突的目标函数：
- 候选解（决策变量）：
f1,f2,....fm对应上面买车的例子的就是价格，油耗，安全性能。基于分解就是把F（x）分解成m个标量化的小目标，求F（x）的最小值，可以转化成求所有的f1,f2,....fm合成的最小值，但是这个时候又会出现一个问题，那就是f1可能是想得到一个最大值，就比如f1为安全性，f2为油耗，f3为价格，则我们把f1转化成求最小值，可以使用取f1的倒数，即f1=1/f1，那么，f1,f2,....fm都是越小越好的，则最后取得的F（x）就是最小的。
- 收敛性：Pareto解集与真实的最优解集（EF）尽可能的接近，越接近越好
- 多样性：沿着EF方向解扩散，即在目标空间中分布范围尽可能广（EF左右 全方位扩散）。由此可见解集的收敛性和多样性是相互冲突的
分解方法：
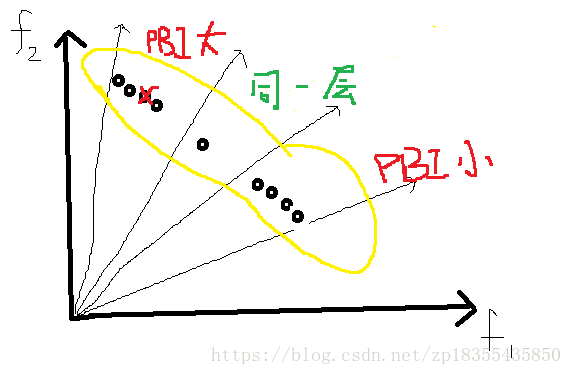
文章中采用的是PBI分解方法
d1用来评价x对EF的收敛性，d2是衡量种群多样性的一种方法。PBI方法的优化问题被定义为：
是用
表示的理想目标向量
MOEA/DD的算法框架：
P为亲本集，W为权向量集，E为领域集
即：1.初始化P,W,E
2.繁殖
3.更新
4.确定P非支配层结构
初始化：
- 初始化P：在可行域中随机均匀的选择N个解为初始亲本种群
- 初始化E:计算当前W与其他各个W的欧氏距离，取前T个欧氏距离最小的值的权向量为当前权向量的邻域（T的值一般都取20）
- 初始化W：权向量，即给每个小目标赋予的权重所组成的向量，
，
且
，权重分量之和等于1，这里的权向量生成方法采用了权向量是通过Das 和Dennis研究的方法一种生成名为Normal-boundary intersection: A new method for generating the Pareto surface in nonlinear multicriteria optimization problems。下面我讲解释一下这个方法：
单纯形：K维单纯形是指包含K+1个节点的凸多面体。
单元单纯形：多面体的每一维坐标取值为1。
权向量将在一个单元单纯形中采样，在单纯形上，可以取S个权重向量，且具有均匀间距1/H，H为沿着每个目标坐标上的划分数，m为维数，则在这个单元单纯形中可以取得
个权重向量。由于
，且它们之间的间距为1/H，可以理解为：在
中取m个值，且这m个值之和为1，可以重复取相同值，则有
种取法。
例如：
设置H=4，m=3的三维空间，每维目标坐标划分为4，则
，会产生15个权向量。如图：
两层权向量生成的方法：边界层（B）和内部层（I），产生的方法还是Das和Dennis方法，只不过内部层产生的权向量要被重新计算之后，再和边界层产生的权向量形成最终的权向量集W。例如：边界层H=2，内层H=1，m=3
- 确定P非支配层结构：使用非支配排序方法。对大小为N的种群进行非支配层排序，每一个解必须和种群中的其他解都进行比较，从而得出它是否被支配，这一步进行完毕之后，找出所有的非支配个体，把它们作为第一层，然后去除这些解，在剩下的解中，继续重复前面的步骤，层数递增，直到找出所有非支配层。最外层为层数最大，为最劣解层。
繁殖：
交配：从当前亲本的权向量邻域里面随机选择一个交配亲本，如果邻域中不存在相关的解，则在整个种群中随机选择交配亲本
变异：在所选择的交配亲本的基础上产生新的子代候选解。变异操作将使用模拟二进制交叉和多项式变异来进行操作，使其达到变异效果
更新：
每次只考虑一个后代解的更新，如果生生成了多个解，那么需要多次执行更新过程。
（1）确定Xc的关联子区域
（2）将Xc的与P形成混合种群
（3）确定P’的非支配层
（4）根据非支配层的层数以及特点分不同的情况进行更新
为子区域，定义为：
可以理解为当前的个体所离的最近的那个权向量周边的区域叫做子区域
更新的时候，消除最劣解有两大情况：
（1）只有一个非支配层L=1
a）先找出密度估计最大（即最拥挤）的子区域 
，如果只有一个最拥挤区域，根据PBI值去删除最差的
b）如果有多个密度估计值最大的子区域，那么找到PBI值之和最大的子区域，作为最拥挤的区域，其中
在 中最坏的解其PBI值最大
（2）有多个非支配层L>1：由于每次只剔除一个最差解，所以我们可以从最后一个非支配层Fl开始进行：
1）| Fl |=1，即最后一层只包含一个解
，我们研究与相关的子区域的密度：
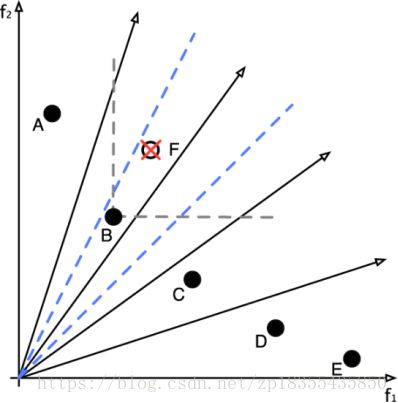
a）如果与 相关的子区域包含一个以上的解，那么就将剔除，因为考虑到收敛性，没有提供比该区域其它解更有 用的信息。如下图中的F点：
b）如果与相关的子区域只包含一个解，而且这个解是与 一个孤立子区域相关联，那么为了种群的多 样性，我们将其保留下来。同时，在最后一层使用（1）中公式（7）先找到最拥挤的区域，从而再利 用公式（8）找出最差的解x’剔除。
2）| Fl |>1，即最后一层包含多个解。先找到与Fl中解相关的最拥挤区域
a）如果=1，即Fl中的每一个成员都与一个孤立子区域 相关联，与1）中的处理方法一样，将这些解都保留到下一代。同时，使用1）b方法剔除最差解x’。
b）如果中包含多个解，直接使用公式（8）剔除最差解