【深度学习】6：RNN递归神经网络原理

前言：自己学习研究完CNN卷积神经网络后，很久的一段时间因为要完成自己的毕业设计就把更新博客给耽搁了。瞎忙了这么久，还是要把之前留的补上来。因为“种一棵树最好的时间是在十年前，其次就是现在！”
–-----------------------------------------------------------------------------—--------------------------------------------------------—----
–-----------------------------------------------------------------------------—--------------------------------------------------------—----

递归神经网络与循环神经网络联系

• CNN卷积神经网络和RNN递归神经网络都是由BP神经网络演化而来的。CNN卷积神经网络主要应用在图像识别领域；而RNN递归神经网络的改进版LSTM网络主要应用于自然语言处理中；
• 为什么我介绍RNN是叫——递归神经网络？这之前是一个困扰我很久的问题。因为在网上搜索RNN既有人说是递归神经网络，也有人说是循环神经网络，而且两个的区别也不明显，混淆很久，直到请教前辈——递归神经网络是从神经网络的运行状态划分的，由下面图示就可以了解到这种神经网络在运行时像是自行迭代；而循环神经网络可以看作是递归神经网络的特例，以示区别就把递归神经网络总称RNN，循环神经网络叫做RNNs。

一、RNN原理介绍

RNN神经网络为什么广泛应用于自然语言处理？因为它是依靠时间序列具有记忆功能的——这一刻的输出，除了考虑这一刻的输入外，还有一部分是来自上一刻的输出记忆。同时这一刻的输出也会有一部分做为“记忆”传给下一刻。

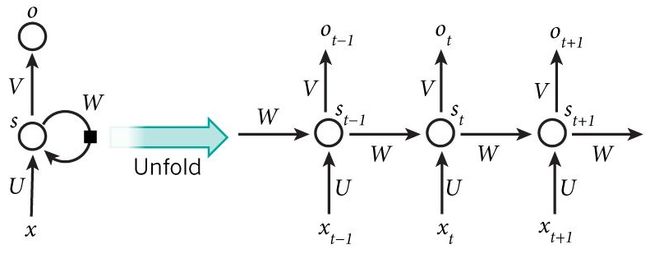
上图是RNN神经网络的结构示意图。上左图是简化过程，介绍从上右图说起：

1. 上右图包含t-1、t、t+1三个时刻的输入与输出；
2. t时刻的输入Xt经权值U、t-1时刻的状态记忆经权值W共同作用构成t时刻的状态St；
3. t时刻的状态St作为一部分记忆经权值W传入下一时刻，也作为t时刻的输出经权值V作用后输出Ot。

形象的比喻——横向的传播就是游戏的主线，游戏过程中不断有纵向的分线任务X传入，每一个分线任务都对主线任务构成影响且都能生成一个预测结果O，最后一个输出O就是游戏的最终结果；

**用RNNs结合MNIST数据集做图片识别，输入的一个X就是MNIST数据集中图片的一行28个像素点数据的向量。**在以下的数据维度说明中有更详细的介绍。

二、用RNNs预测MNIST数据

之前介绍了BP神经网络、CNN卷积神经网络用MNIST数据集做图像识别，现在介绍用RNNs循环神经网络也是用MNIST数据集做图像识别。这个识别原理也非常有趣。（详细解析处代码都是伪代码，源代码在最后附上）

RNNs做图像识别原理：MNIST数据集中一张图片数据包含28*28的像素点。RNNs是将一张图片数据的一行作为一个向量总体输入一个X中。也就是说，RNNs有28个输入X，一个输入X有28个像素点。t=1时刻输入X1，得到中间状态S1，由S1得到预测值O1（现在的O1由于只考虑一张图片的一行数据而已，预测结果很不可靠），S1也作为一部分记忆，再与图片下一行的输入X2相作用，得到中间状态S2，再得到预测值O2…循环迭代，直到将一张图片的28行全都代入，输出最后一个O28做为预测值。

2.1：MNIST数据集的读取

from tensorflow.examples.tutorials.mnist import input_data	
mnist = input_data.read_data_sets('MNIST_data',one_hot = True)
batch_size = 100
batch_xs,batch_ys = mnist.train.next_batch(batch_size)

这个MNIST数据集的读取我已经介绍了好多好多次了…如果本目录下没有MNIST数据集，程序会自动下载。读取的数据先存入“mnist”数组中，并按照每100个图片作为一个批次，将训练集的图片数据存入“batch_xs”数组，图片标签项存入“batch_ys ”。

2.2：输入数据维度说明

n_inputs = n_steps = 28
# batch_xs shape = [100,28,28]
X = batch_xs.reshape([batch_size,n_steps,n_inputs])
...
# X shape = (100batch,28steps,28inputs) ==> (100batch*28steps,28inputs)
X = tf.reshape(X,[-1,n_inputs])
# X_in shape ==> (100batch*28steps,128hidden)
X_in = tf.matmul(X,weights['in'])+biases['in']
# X_in shape ==> (100batch,28steps,128hidden)
X_in = tf.reshape(X_in,[-1,n_steps,n_hidden_number])

这里可以说是很烦人的地方了，输入数据的维度出错程序总是报错，真的烦了很久：（因为批次的原因使得数据变成三维，而权重阈值计算是二维的）

• 之前我们确定的每一个批次有100张图片数据，就相当于将100张28*28的图片叠放在一起，读取的就是一个三维立体的整体（长宽都是28，高100）。所以第3行代码先将读取的整批图片切割成[100,28,28]的单个图片；
• 依据上面介绍的RNNs做图像识别的原理出发，每个输入X都是一张图片的一行，再构造与图片行数相同个数的输入神经元就可以完成一张图片的识别。但现在是100张图片一起识别，就需要将三维立体的整体数据转化为二维才能与阈值、权重代入计算，第6行代码就是降维运算；
• 经过降维运算，RNNs神经网络输入层28个神经元中每一个神经元输入的维度是10028，经过第8行权值阈值处理后，得到X_in。（隐藏层有128个神经元，所以X_in此时维度是[10028，128]）
• 再将得到的X_in切割成[100，28，128]，继续后续cell核运算

2.3：RNNs的核运算

首先说明：这个“核运算”是我为书写方便自创的

lstm_cell = tf.nn.rnn_cell.BasicLSTMCell(n_hidden_number,forget_bias = 1.0)
# LSTM cell is divided into two parts(c_state,m_state)
init_state = lstm_cell.zero_state(batch_size,dtype=tf.float32)
outputs,states = tf.nn.dynamic_rnn(lstm_cell,X_in,initial_state=init_state,time_major=False)

这个核运算也是基于TensorFlow框架。

• 首先创建RNN运算核——lstm_cell，选择的cell是BasicLSTMCell（tf.nn.rnn中有许多，这里不做介绍），参数是隐藏层神经元个数；
• RNN的中间状态会得到两部分——一个是当前输出outputs，另一个是下时刻的记忆states，RNN在init_state中用c_state、m_state分别保存这两部分；
• 用dynamic_rnn的方法，用输入值X_in进行核内运算，将输出分别存入相应数组中。

2.4：计算输出

result = tf.matmul(states[1],weights['out'])+biases['out']

• 在核内以X_in为输入，得到输出outputs与states，当所有行都代入计算得到最后的输出预测值。其中states[1] = outputs[-1]，相当于最后一个输出值。

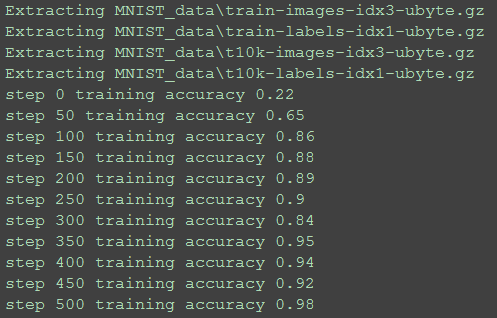
三、源码与效果展示

# -*- coding:utf-8 -*-
# -*- author：zzZ_CMing
# -*- 2018/02/05；09:58
# -*- python3.5

from tensorflow.examples.tutorials.mnist import input_data
import tensorflow as tf
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'

mnist = input_data.read_data_sets('MNIST_data',one_hot = True)

training_iters = 50001
batch_size = 100          #批量大小

n_inputs = n_steps = 28
n_hidden_number = 128    #隐藏层神经元个数
n_outputs = 10           #输出层神经元个数

x = tf.placeholder(tf.float32,[None,n_steps,n_inputs])
Y = tf.placeholder(tf.float32,[None,n_outputs])

weights = {
    # shape = (28,128)
    'in':tf.Variable(tf.random_normal([n_inputs,n_hidden_number])),
    # shape = (128,10)
    'out':tf.Variable(tf.random_normal([n_hidden_number,n_outputs]))}

biases = {
    # shape = (128,)
    'in':tf.Variable(tf.constant(0.1,shape = [n_hidden_number,])),
    # shape = (10,)
    'out':tf.Variable(tf.constant(0.1,shape = [n_outputs,]))}


def RNN(X,weights,biases):
    ### 输入层到核运算 ###
    # X shape = (100batch,28steps,28inputs) ==> (100batch*28steps,28inputs)
    X = tf.reshape(X,[-1,n_inputs])
    # X_in shape ==> (100batch*28steps,128hidden)
    X_in = tf.matmul(X,weights['in'])+biases['in']
    # X_in shape ==> (100batch,28steps,128hidden)
    X_in = tf.reshape(X_in,[-1,n_steps,n_hidden_number])

    ### cell核内运算 ###
    lstm_cell = tf.nn.rnn_cell.BasicLSTMCell(n_hidden_number,forget_bias = 1.0)
    # LSTM cell is divided into two parts-->(c_state,m_state)
    init_state = lstm_cell.zero_state(batch_size,dtype=tf.float32)
    outputs,states = tf.nn.dynamic_rnn(lstm_cell,X_in,initial_state=init_state,time_major=False)

    ### 核内运算到输出层 ###
    result = tf.matmul(states[1],weights['out'])+biases['out']
    return  result


prediction = RNN(x,weights,biases)
#二次代价函数:预测值与真实值的误差
loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=Y, logits=prediction))
#梯度下降法:数据庞大,选用AdamOptimizer优化器
train_step = tf.train.AdamOptimizer(1e-3).minimize(loss)
#结果存放在一个布尔型列表中
correct_prediction = tf.equal(tf.argmax(prediction,1), tf.argmax(Y,1))
#求准确率
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))

init = tf.global_variables_initializer()
with tf.Session() as sess:
    sess.run(init)
    step = 0
    while step*batch_size < training_iters:
        batch_xs,batch_ys = mnist.train.next_batch(batch_size)
        # batch_xs shape = [100,28,28]
        batch_xs = batch_xs.reshape([batch_size,n_steps,n_inputs])
        train_step.run(feed_dict={x:batch_xs,Y:batch_ys,})
        if step%50 == 0:
            train_accuracy = accuracy.eval(feed_dict={x:batch_xs,Y:batch_ys,})
            print("step", step, "training accuracy", train_accuracy)
        step += 1

效果展示：

–-----------------------------------------------------------------------------—--------------------------------------------------------—----
–-----------------------------------------------------------------------------—--------------------------------------------------------—----

系列推荐：

【监督学习】1：KNN算法实现手写数字识别的三种方法
–-----------------------------------------------------------------------------—--------------------------------------------------------—----
【无监督学习】1：K-means算法原理介绍，以及代码实现
【无监督学习】2：DBSCAN算法原理介绍，以及代码实现
【无监督学习】3：Density Peaks聚类算法（局部密度聚类）
–-----------------------------------------------------------------------------—--------------------------------------------------------—----
【深度学习】1：感知器原理，以及多层感知器解决异或问题
【深度学习】2：BP神经网络的原理，以及异或问题的解决
【深度学习】3：BP神经网络识别MNIST数据集
【深度学习】4：BP神经网络+sklearn实现数字识别
【深度学习】5：CNN卷积神经网络原理、MNIST数据集识别
【深度学习】8：CNN卷积神经网络识别sklearn数据集（附源码）
【深度学习】6：RNN递归神经网络原理、MNIST数据集识别
【深度学习】7：Hopfield神经网络（DHNN）原理介绍
–-----------------------------------------------------------------------------—--------------------------------------------------------—----
TensorFlow框架简单介绍
–-----------------------------------------------------------------------------—--------------------------------------------------------—----