熄灯问题-枚举

OpenJudge-NOI/2.1基本算法之枚举-1813:熄灯问题

总时间限制: 1000ms 内存限制: 65536kB

描述

有一个由按钮组成的矩阵，其中每行有6个按钮，共5行。每个按钮的位置上有一盏灯。当按下一个按钮后，该按钮以及周围位置(上边、下边、左边、右边)的灯都会改变一次。即，如果灯原来是点亮的，就会被熄灭；如果灯原来是熄灭的，则会被点亮。在矩阵角上的按钮改变3盏灯的状态；在矩阵边上的按钮改变4盏灯的状态；其他的按钮改变5盏灯的状态。

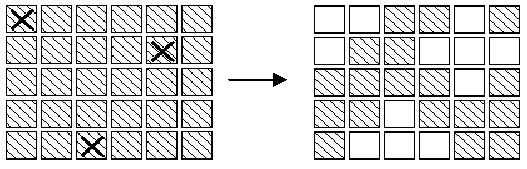
在上图中，左边矩阵中用X标记的按钮表示被按下，右边的矩阵表示灯状态的改变。对矩阵中的每盏灯设置一个初始状态。请你按按钮，直至每一盏等都熄灭。与一盏灯毗邻的多个按钮被按下时，一个操作会抵消另一次操作的结果。在下图中，第2行第3、5列的按钮都被按下，因此第2行、第4列的灯的状态就不改变。

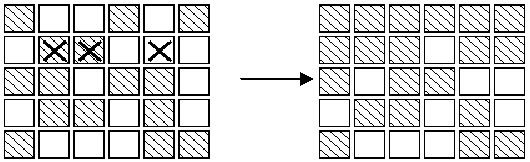
请你写一个程序，确定需要按下哪些按钮，恰好使得所有的灯都熄灭。根据上面的规则，我们知道1）第2次按下同一个按钮时，将抵消第1次按下时所产生的结果。因此，每个按钮最多只需要按下一次；2）各个按钮被按下的顺序对最终的结果没有影响；3）对第1行中每盏点亮的灯，按下第2行对应的按钮，就可以熄灭第1行的全部灯。如此重复下去，可以熄灭第1、2、3、4行的全部灯。同样，按下第1、2、3、4、5列的按钮，可以熄灭前5列的灯。

输入

5行组成，每一行包括6个数字（0或1）。相邻两个数字之间用单个空格隔开。0表示灯的初始状态是熄灭的，1表示灯的初始状态是点亮的。

输出

5行组成，每一行包括6个数字（0或1）。相邻两个数字之间用单个空格隔开。其中的1表示需要把对应的按钮按下，0则表示不需要按对应的按钮。

样例输入

0 1 1 0 1 0
1 0 0 1 1 1
0 0 1 0 0 1
1 0 0 1 0 1
0 1 1 1 0 0

样例输出

1 0 1 0 0 1
1 1 0 1 0 1
0 0 1 0 1 1
1 0 0 1 0 0
0 1 0 0 0 0

题解

首先，我们会想到暴力枚举，枚举所有可能的按钮（开关）的状态，然后对每个状态计算一下灯的最后情况，看所有灯是否都熄灭。
每个按钮有两种状态，按下或者不按下，一共有30个按钮，那么状态数就是2的30次方，如果真的要写那么就会有30重循环，这样就太多了，肯定会超时。
这里说一下，这道题的总体思路和我写的上一篇博客拨钟问题类似，但拨钟问题可以通过暴力枚举做出来并且不超时，因为拨钟问题暴力枚举只是一个九重循环，远远少于这道题的30重循环，有兴趣的话可以去看看我写的拨钟问题。

所以这就有了一个问题，怎么减少枚举的状态数目呢？
基本思路如下：
如果存在某个局部, 一旦这个局部的状态被确定, 那么剩余其他部分的状态只能是确定的一种, 或者不多的n 种, 那么就只需枚举这个局部的状态即可
局部思想这种思维十分的重要！
本题是否存在这样的 “局部” 呢? 经过观察发现，第1行就是这样的一个 “局部” 。
因为第1行的各开关状态确定的情况下, 这些开关作用过后, 将导致第1行某些灯是亮的, 某些灯是灭的。要熄灭第1行某个亮着的灯(假设位于第i列), 那么唯一的办法就是按下第2行第i列的开关。（因为第1行的开关已经作用过了, 而第3行及其后的开关不会影响到第1行），为了使第1行的灯全部熄灭，第2行的合理开关状态就是唯一的。
同理，第2行的开关起作用后，为了熄灭第2行的灯，第3行的合理开关状态就也是唯一的。以此类推，最后一行的开关状态也是唯一的。所以只要第1行的状态定下来，假若我们把它记作A，那么剩余行的情况就是唯一确定的了。最后我们推算出最后一行的开关状态，然后看看最后一行的开关起作用后, 最后一行的所有灯是否都熄灭：如果是，那么A就是一个解的状态。如果不是，那么A不是解的状态，第1行换个状态重新试试。
综上所述，只需枚举第一行的状态，状态数为2的6次方=64。
有没有状态数更少的做法？枚举第一列，状态数为2的5次方=32。

根据上述题解，我们有以下的具体实现方案：

方案一 采用二维数组

代码如下：

#include
#include
using namespace std;
int puzzle[6][8];
int press[6][8];

bool guess()  
{
	int r,c;
	for(r=1; r<5; r++)
		for(c=1; c<7; c++)
			press[r+1][c]=(press[r][c]+press[r][c-1]+press[r][c+1]+press[r-1][c]+puzzle[r][c])%2;
	for(c=1; c<7; c++)
	{
		if(puzzle[5][c] != ((press[5][c-1]+press[5][c]+press[5][c+1]+press[4][c])%2))
			return false;
	}
	return true;	
} 

void enumerate()
{
	int c;
	for(c=1; c<7; c++)
		press[1][c]=0;
	while(guess()==false)
	{
		press[1][6]++;
		c=6;
		while(press[1][c]>1)
		{
			press[1][c]=0;
			c--;
			press[1][c]++;
		}
	}
	return;
}

int main()
{
	//freopen("D:\\C++\\OpenJudge\\NOI\\in.txt","r",stdin);
	int r,c;
	for(r=0; r<6; r++)
		press[r][0]=press[r][7]=0;
	for(c=1; c<7; c++)
		press[0][c]=0;
	for(r=1; r<6; r++)
		for(c=1; c<7; c++)
			cin >> puzzle[r][c];
	enumerate();
	for(r=1; r<6; r++)
	{
		for(c=1; c<7; c++)
		{
			cout << press[r][c] << " ";
		}
		cout << endl;
	}
	return 0;
}

代码注释：

/*
r:row    行  
c:column 列 
*/
#include
#include
using namespace std;
int puzzle[6][8];//存储灯的初始状态，0表示灯是熄灭的，1表示灯是被点亮的 
int press[6][8];//存储最后计算的结果，0表示不按按钮，1表示按按钮 

bool guess()//判断确定好第一行按钮的状态后，推算第五行灯是否全熄灭   
{
	int r,c;
	for(r=1; r<5; r++)//根据 press第一行和 puzzle数组，计算 press其他行的值
		for(c=1; c<7; c++)
			press[r+1][c]=(press[r][c]+press[r][c-1]+press[r][c+1]+press[r-1][c]+puzzle[r][c])%2;
	for(c=1; c<7; c++)//判断所计算的 press数组能否熄灭第5行的所有灯
	{
		if(puzzle[5][c] != ((press[5][c-1]+press[5][c]+press[5][c+1]+press[4][c])%2))
			return false;
	}
	return true;	
} 

void enumerate()//枚举 将矩阵第一行看成一个二进制数从 000000 - 111111  (0-63) 共64种状态
{
	int c;
	for(c=1; c<7; c++)
		press[1][c]=0;
	while(guess()==false)//如果到最后一行时灯未全部熄灭(guess()==false)，则将第一行（第一行看成一个二进制数）进行++，换种状态进行枚举
	{
		press[1][6]++;
		c=6;
		while(press[1][c]>1)
		{
			press[1][c]=0;
			c--;
			press[1][c]++;
		}
	}
	return;
}

int main()
{
	//freopen("D:\\C++\\OpenJudge\\NOI\\in.txt","r",stdin);
	int r,c;
	for(r=0; r<6; r++)//第0列和第7列置为0
		press[r][0]=press[r][7]=0;
	for(c=1; c<7; c++)//第0行置为0
		press[0][c]=0;
	for(r=1; r<6; r++)
		for(c=1; c<7; c++)
			cin >> puzzle[r][c];
	enumerate();
	for(r=1; r<6; r++)
	{
		for(c=1; c<7; c++)
		{
			cout << press[r][c] << " ";
		}
		cout << endl;
	}
	return 0;
}

总结：此算法核心为enumerate()和guess()这两个函数。
1.枚举过程enumerate()这个函数作用是枚举第一行状态数，将press数组第一行看成一个二进制数，左边高位，右边低位，通过模拟二进制加法方式实现枚举，从000000到111111，过程如下所示：

0 0 0 0 0 0
0 0 0 0 0 1
0 0 0 0 1 0
0 0 0 0 1 1
0 0 0 1 0 0
0 0 0 1 0 1
......
1 1 1 1 1 1

2.推测验证过程guess()这个函数作用是判断确定好第一行按钮的状态后，推算第五行灯是否全熄灭。其中用一个6x8的按钮矩阵来简化一下按钮值的计算公式，并根据press[1][]和puzzle数组，用公式来计算使得1-4行所有灯熄灭的press其他行的值，再判断所计算的press数组能否熄灭矩阵第五行的所有灯。

若此方案想了解更多请参考这篇博客：
https://blog.csdn.net/NNNNNNNNNNNNY/article/details/51584247

方案二 采用位运算

因为灯只有两种状态，被点亮或者熄灭，并且题目中已经说了0表示灯的初始状态是熄灭的，1表示灯的初始状态是点亮的。只有0和1，故很容易想到二进制，进而想到用位运算去解决这道问题。我们可以将一行灯的状态用一个char类型的变量去存储，char类型变量占用存储空间为1个字节也就是8位，取其低六位来表示一行灯的状态，每位为一盏灯的状态。一共有5行所以只需用含五个元素的char类型一维数组来存储，开关状态同理。

代码如下：

#include
#include
#include 
using namespace std;
int GetBit(char c,int i)
{
	return (c >> i) & 1;
}

void SetBit(char & c,int i,int v)
{
	if(v)
		c |= (1 << i);
	else
		c &= ~(1 << i); 
}

void Flip(char & c,int i)
{
	c ^= (1 << i);
}

void Output(char result[])
{
	for(int r=0; r<5; r++)
	{
		for(int c=0; c<6; c++)
		{
			cout << GetBit(result[r],c) << " ";
		}
		cout << endl;
	}
}

int main()
{
	//freopen("D:\\C++\\OpenJudge\\NOI\\in.txt","r",stdin);
	char orilights[5];
	char lights[5];
	char result[5];
	char buttons;
	memset(orilights,0,sizeof(orilights));
	for(int r=0; r<5; r++)
		for(int c=0; c<6; c++)
		{
			int v;
			cin >> v;
			SetBit(orilights[r],c,v);
		}
	for(int n=0; n<64; n++)
	{
		memcpy(lights,orilights,sizeof(orilights));
		buttons=n;
		for(int r=0; r<5; r++)
		{
			result[r]=buttons;
			for(int c=0; c<6; c++)
			{
				if(GetBit(buttons,c))
				{
					if(c>0)
						Flip(lights[r],c-1);
					if(c<5)
						Flip(lights[r],c+1); 
					Flip(lights[r],c); 
				}
			}
			if(r<4)
			{
				lights[r+1] ^= buttons; 
			}
			buttons = lights[r];
		}
		if(lights[4]==0)
		{
			Output(result);
			break;
		}
	}
	return 0;
}

代码注释：

#include
#include
#include 
using namespace std;
int GetBit(char c,int i)//取c的第i位 
{
	return (c >> i) & 1;
}

void SetBit(char & c,int i,int v)//设置c的第i位为v 
{
	if(v)
		c |= (1 << i);
	else
		c &= ~(1 << i); 
}

void Flip(char & c,int i)//将c的第i位取反 
{
	c ^= (1 << i);
}

void Output(char result[])//输出结果 
{
	for(int r=0; r<5; r++)
	{
		for(int c=0; c<6; c++)
		{
			cout << GetBit(result[r],c) << " ";
		}
		cout << endl;
	}
}

int main()
{
	//freopen("D:\\C++\\OpenJudge\\NOI\\in.txt","r",stdin);
	char orilights[5];//最初灯矩阵，一个比特表示一盏灯 
	char lights[5];//不停变化的灯矩阵 
	char result[5];//最后计算的结果按钮矩阵 
	char buttons;//某一行的（按钮）开关状态 
	memset(orilights,0,sizeof(orilights));
	for(int r=0; r<5; r++)//读入最初灯状态 
		for(int c=0; c<6; c++)
		{
			int v;
			cin >> v;
			SetBit(orilights[r],c,v);
		}
	for(int n=0; n<64; n++)//遍历首行开关的64种状态，从 000000 - 111111
	{
		memcpy(lights,orilights,sizeof(orilights));
		buttons=n;//首行开关状态 
		for(int r=0; r<5; r++)
		{
			result[r]=buttons;//第i行的开关方案 
			for(int c=0; c<6; c++)
			{
				if(GetBit(buttons,c))
				{
					if(c>0)
						Flip(lights[r],c-1);//改左灯 
					if(c<5)
						Flip(lights[r],c+1);//改右灯 
					Flip(lights[r],c);//改开关位置的灯 
				}
			}
			if(r<4)
			{
				lights[r+1] ^= buttons;//改下一行的灯  
			}
			buttons = lights[r];//第i+1行开关方案和第i行灯情况相同
		}
		if(lights[4]==0)//如果第5行灯全熄灭也就是全为0，那么就输出result
		{
			Output(result);
			break;
		}
	}
	return 0;
}

最后，再强调一下，两种方案虽然实现过程不一样，一个采用二维数组实现，一个采用位运算实现，但是采用的思想都是一样的，都是局部思维，只用枚举一个局部即可，这道题的局部就是第一行。

此题的两种实现方案并非原创，而是出自北京大学的郭炜老师，郭老师牛逼！！！大家也可以去中国大学MOOC上学习郭炜老师的算法课程。
感谢阅读，若有错误还请指出，如果有什么不懂的也可以留言。