图像处理理论（八）——Meanshift, Camshift, Optical flow

Meanshift

Meanshift聚类

Meanshift（均值漂移）首先是个聚类算法，然后才应用到目标跟踪领域。它是Keinosuke Fukunaga和Larry D. Hostetler于1975年发明的。

Keinosuke Fukunaga，日本裔美国科学家，普渡大学教授。著有《Introduction to Statistical Pattern Recognition》一书。

我们首先来定义一下Mean Shift向量。

对于给定的d维空间 Rd R d 中的n个样本点 xi,i=1,⋯,n x i , i = 1 , ⋯ , n ，则对于x点，其Mean Shift向量的基本形式为：

Mh(x)=1k∑xi∈Sh(xi−x) M h ( x ) = 1 k ∑ x i ∈ S h ( x i − x )

其中， Sh S h 指的是一个半径为h的高维球区域，如上图中的蓝色的圆形区域。 Sh S h 的定义为：

Sh(x)=(y∣(y−x)(y−x)T⩽h2) S h ( x ) = ( y ∣ ( y − x ) ( y − x ) T ⩽ h 2 )

从物理的角度来看，由于 1k∑xi∈Shxi 1 k ∑ x i ∈ S h x i 实际上是 Sh S h 的质量中心，因此 Mh(x) M h ( x ) 实际上就是从x指向质心的向量，也被叫做归一化的概率密度梯度。所以，Meanshift聚类实际上是一种密度聚类。

下面来看一下Meanshift算法的具体步骤。

首先，在空间中任选一点x（上图中蓝色的圈），以x为圆心，h为半径做一个高维球（上图中蓝色的圆）。计算得到质心（上图中黄色的圈）。移动x到质心，并重复之前的步骤。最终x会收敛到最密集区域的质心。

基本的Mean Shift形式存在一个问题：在 Sh S h 的区域内，每一个点对x的贡献是一样的。而实际上，这种贡献与x到每一个点之间的距离是相关的。同时，对于每一个样本，其重要程度也是不一样的。

到了1995年，Yizong Cheng（现为University of Cincinnati副教授）对基本的Mean Shift算法在以下两个方面做了推广。

首先，定义了一族核函数,使得随着样本与被偏移点的距离不同,其偏移量对均值偏移向量的贡献也不同。

其次，还设定了一个权重系数,使得不同的样本点重要性不一样,这大大扩大了Mean Shift的适用范围。

基于以上的考虑，可对基本的Mean Shift向量形式中增加核函数和样本权重，得到如下的改进的Mean Shift向量形式：

Mh(x)=∑ni=1GH(xi−x)w(xi)(xi−x)∑ni=1GH(xi−x)w(xi) M h ( x ) = ∑ i = 1 n G H ( x i − x ) w ( x i ) ( x i − x ) ∑ i = 1 n G H ( x i − x ) w ( x i )

其中：

GH(xi−x)=|H|−12G(H−12(xi−x)) G H ( x i − x ) = | H | − 1 2 G ( H − 1 2 ( x i − x ) )

G(x)是一个单位的核函数。H是一个正定的对称d×d矩阵，称为带宽矩阵，其是一个对角阵。 w(xi)⩾0 w ( x i ) ⩾ 0 是每一个样本的权重。对角阵H的形式为：

H=⎛⎝⎜⎜⎜⎜⎜h210⋮00h22⋮0⋯⋯⋯00⋮h2d⎞⎠⎟⎟⎟⎟⎟d×d H = ( h 1 2 0 ⋯ 0 0 h 2 2 ⋯ 0 ⋮ ⋮ ⋮ 0 0 ⋯ h d 2 ) d × d

因此，上述Mean Shift向量也可以改写成：

Mh(x)=∑ni=1G(xi−xhi)w(xi)(xi−x)∑ni=1G(xi−xhi)w(xi) M h ( x ) = ∑ i = 1 n G ( x i − x h i ) w ( x i ) ( x i − x ) ∑ i = 1 n G ( x i − x h i ) w ( x i )

这里的核函数可以是Uniform核，也可以是Gaussian核。

参考：

https://wenku.baidu.com/view/5862334827d3240c8447ef40.html

meanshift算法简介

http://www.cnblogs.com/liqizhou/archive/2012/05/12/2497220.html

Meanshift，聚类算法

https://wenku.baidu.com/view/0d9eb876a417866fb84a8eb2.html

mean-shift算法概述

http://www.cnblogs.com/cfantaisie/archive/2011/06/10/2077188.html

meanshift聚类

https://blog.csdn.net/google19890102/article/details/51030884

Mean Shift聚类算法

反向投影图

在继续介绍Meanshift之前，我们先引入反向投影图的概念。

首先，我们对图像的像素值按照某种特征进行直方图统计，得到一组bin值。

然后，计算位置x上的bin值，并用该bin值替换原来的像素值，就得到了反向投影图。

参考：

https://blog.csdn.net/poiiy333/article/details/9051409

反向投影图

Meanshift与目标跟踪

由于RGB对光照的变化比较敏感，而这种敏感对目标跟踪而言是不利的。因此，通常我们要将图像转换到HSV颜色空间。

首先，统计目标box区域内H（色调）分量的直方图，并对其进行归一化，使得该直方图成为概率直方图。这一步相当于统计目标的颜色特征。

然后，使用统计得到的概率直方图，将全图转换为反向投影图，并应用Meanshift算法。由于前后两帧中目标通常不会隔的太远，原目标中心可能仍在目标范围内。因此，目标中心会向反向投影图中概率大的地方移动，从而达到了目标跟踪的效果。

总结：用meanshift进行跟踪最重要的一点是输入图像的把握，也就是要让它的迭代能越来越迭代到目标上。这种图像也不一定就是反向投影图，只要是一幅反映当前图像中每个像素点含有目标概率的图就可以了。反向投影图恰好就是这样的一幅图而已。

优点：

（1）算法计算量不大，在目标区域已知的情况下完全可以做到实时跟踪；

（2）采用核函数直方图模型，对边缘遮挡、目标旋转、变形和背景运动不敏感。

缺点：

（1）缺乏必要的模板更新；

（2）跟踪过程中由于窗口宽度大小保持不变，当目标尺度有所变化时，跟踪就会失败；

（3）当目标速度较快时，跟踪效果不好；

（4）直方图特征在目标颜色特征描述方面略显匮乏，缺少空间信息；

参考：

https://blog.csdn.net/li_dongxuan/article/details/70667170

目标跟踪：Meanshift, Camshift

http://www.cnblogs.com/cfantaisie/archive/2011/06/10/2077190.html

meanshift目标跟踪算法总结

https://blog.csdn.net/jinshengtao/article/details/30258833

基于MeanShift的目标跟踪算法及实现

Meanshift与图像分割

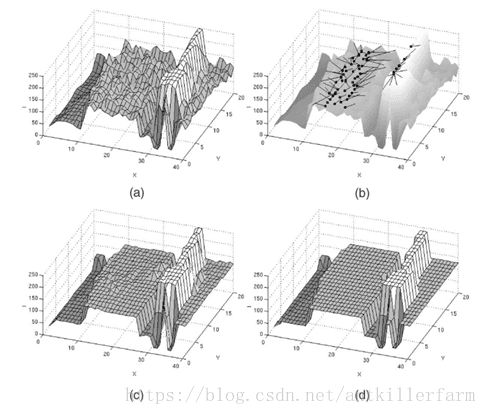
除此之外，mean shift还可以用于图像分割。

如上图所示，算法过程可分三步走：模点搜索/图像平滑、模点聚类/合并相似区域、兼并小区域（可选）。

模点搜索是为了找到每个数据点的到类中心，以中心的颜色代替自己的颜色，从而平滑图像。

但模点搜索得到的模点太多，并且很多模点挨得很近，若果将每个模点都作为一类的话，类别太多，容易产生过分割，即分割太细，所以要合并掉一些模点，也就是合并相似区域。

模点聚类后所得到的分割区域中，有些区域所包含的像素点太少，这些小区域也不是我们想要的，需要再次合并。

参考：

https://blog.csdn.net/ttransposition/article/details/38514127

mean shift图像分割

Camshift

Camshift算法是Continuously Adaptive Mean Shift algorithm的简称。它是一个基于MeanSift的改进算法。它首次由Gary R.Bradski等人提出和应用在人脸的跟踪上，并取得了不错的效果。

由于Meanshift在跟踪中搜索框的大小一直不变，对目标的尺度变化不具有鲁棒性。Camshift针对此点设计了自适应算法用于调整窗口的大小。该方法共有两步：

扩大：在计算窗口大小前，在MeanShift算出的窗口的四个方向上增大了TOLERANCE，即高和宽都增大了2TOLERANCE（此值自己调整设置）。

缩小：在扩大的窗口内重新计算0阶矩，1阶矩和2阶矩，利用矩的值重新计算高和宽。

缺点：

（1）只利用颜色统计做的跟踪，在背景有相似颜色时，会出现跟踪错误的情况。

（2）不能做多目标跟踪。

（3）由于它只在初始位置（而不是从每个像素点）开始迭代，所以有可能在初始位置错了后，收敛的位置还是原位置（即跟丢了后，可能会找不回来）。

参考：

http://blog.sina.com.cn/s/blog_5d1476580101a57j.html

Camshift算法

http://blog.163.com/thomaskjh@126/blog/static/370829982010113133152722/

CAMSHIFT原理

https://wenku.baidu.com/view/59596ac42cc58bd63186bd37.html

Camshift算法原理

Optical flow

基本概念

从本质上说，光流就是你在这个运动着的世界里感觉到的明显的视觉运动。例如，当你坐在火车上，然后往窗外看。你可以看到树、地面、建筑等等，他们都在往后退。这个运动就是光流。

一些比较远的目标，例如云、山，它们移动很慢，感觉就像静止一样。但一些离得比较近的物体，例如建筑和树，就比较快的往后退，然后离我们的距离越近，它们往后退的速度越快。可以通过不同目标的光流运动速度判断它们与我们的距离。

光流除了提供远近外，还可以提供角度信息。与咱们的眼睛正对着的方向成90度方向运动的物体速度要比其他角度的快。

以上是光流的一个直观的定义和特性，下面谈一下它的严谨的研究性定义。

光流的概念是Gibson在1950年首先提出来的。它是空间运动物体在观察成像平面上的像素运动的瞬时速度，是利用图像序列中像素在时间域上的变化以及相邻帧之间的相关性来找到上一帧跟当前帧之间存在的对应关系，从而计算出相邻帧之间物体的运动信息的一种方法。一般而言，光流是由于场景中前景目标本身的移动、相机的运动，或者两者的共同运动所产生的。

当人的眼睛观察运动物体时，物体的景象在人眼的视网膜上形成一系列连续变化的图像，这一系列连续变化的信息不断“流过”视网膜（即图像平面），好像一种光的“流”，故称之为光流（optical flow）。光流表达了图像的变化，由于它包含了目标运动的信息，因此可被观察者用来确定目标的运动情况。

研究光流场的目的就是为了从图片序列中近似得到不能直接得到的运动场。运动场（motion field），其实就是物体在三维真实世界中的运动；光流场，是运动场在二维图像平面上（人的眼睛或者摄像头）的投影。

光流约束方程

1981年，Horn和Schunck创造性地将二维速度场与灰度相联系，引入光流约束方程，得到光流计算的基本算法。人们基于不同的理论基础提出各种光流计算方法，算法性能各有不同。Barron等人对多种光流计算技术进行了总结，按照理论基础与数学方法的区别把它们分成四种：基于梯度的方法、基于匹配的方法、基于能量的方法、基于相位的方法。近年来神经动力学方法也颇受学者重视。