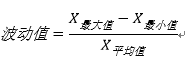用户流失预警模型——LM神经网络+CART决策树

据当代市场学权威菲利普.科特勒研究结论，若一个公司的用户流失率降低5%，则利润将会增加25%-85%。企业若想获得一位新客户，成本往往比挽留一位存量客户所用的成本要高，运营商行业挽留一位有拆机倾向的客户往往只需一个电话或者一个优惠政策即可。本文针对近期争议颇高的不限量套餐用户展开，通过数据挖掘模型对历史数据进行建模，对有流失风险的用户进行精准定位。

我们把该命题归结为如下2个问题：

• 问题1：预测哪些客户（尤其是高价值客户）可能会流失?
• 问题2：可能流失客户的特征是什么?

当然，如果考虑成本费用问题，可以衍生问题3，市场挽留活动的预计收益是什么。

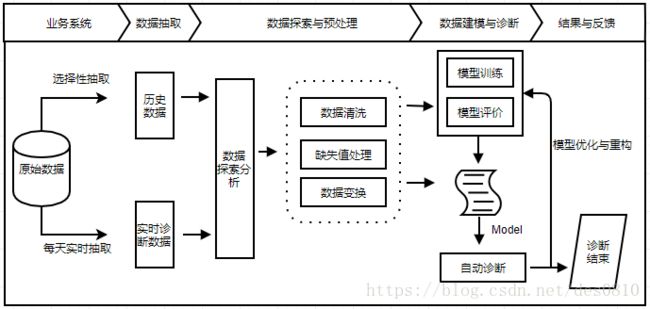
流失用户识别主要包括以下步骤

本案例共抽取了过去10个月的历史数据，累计813683条记录，其中前8个月数据作为模型训练数据，后选取1月数据作为模型测试数据，选取1月数据作为模型检验数据。

注：训练数据是指数据挖掘过程中用于训练数据挖掘模型的数据。训练数据选择一般有以下要求：数据样本尽可能大、数据多样化，数据样本质量较高。测试数据用于模型检验，检验数模作为评估模型的准确率。

1. 数据抽取与数据变换

在数据准备阶段，我们需要考虑有哪些描述用户的数据可以作为预测用户流失变量，包含两个类别数据，分别为：

• 用户基本信息数据：包含用户类型，用户入网时间，用户办理套餐，套餐积分等，这类基本数据一般都可以从业务系统数据库获得。
• 用户行为数据：主要是用户使用电信产品的行为数据，包括用户通话时长，用户使用流量，用户收入等。

为了取得良好的数据挖掘效果，我们偶尔需要对数据进行变化或者生产相关的衍生变量。下面总结一些常用的衍生变量的方法。

• 强度相对指标：有一定联系的的两个指标之间相比的结果的到的指标，如通话时长和通话次数两个指标相比，得到每次通话时长，使我们了解用户的通话习惯，是长话短说型，还是短话长说型。
• 比例相对指标：用来反映总体中各个部分所占比例的一个指标，例如通话时长的被动通话时长和主叫通话时长占比。
• 汇总类指标：在本案例中，一个用户对应有10个月的数据，对应着10条记录，而对应一条是否流失记录，为了便于建立挖掘模型，我们需要将这6条数据变为1条数据，可以根据变量求和、计算平均值、最大值、最小值、标准差等汇总指标。
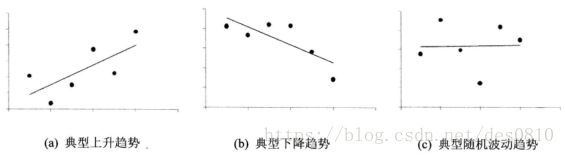
• 趋势类指标：对于时间序列变量而言，最重要的方面是看趋势，如针对收入这个变量，即看一个用户收入在10月期间是变多了还是变少了，还是随机性波动? 我们有理由假设假如一个用户收入变少，是否更有可能流失。 

其中x代表月份，y代表待计算趋势的字段，如收入 ，n代表月份数。序列常见的趋势有：

• 波动类指标：对时间序列而言，趋势只反映了大致方向，而波动类指标衡量波动大小。本案例波动值计算公式如下：

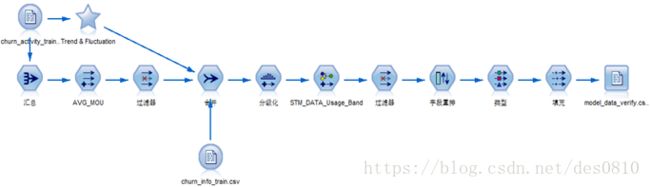
本案例数据变化通过Spss Modeler实现，流程图如下：

2. 数据探索性分析 

• 离散型变量的探索性分析方法：离散变量可通过频数分布表，饼图，条形图等可视化变量取值以及各个取值占比是多少。
• 连续型变量的探索型分析方法：使用描述统计量，如反映集中趋势指标有均值，中位数等，反映趋势和离散程度的标准差、级差等；使用图形，如直线图，核密度估计图等

注： kdeplot(核密度估计图):

核密度估计(kernel density estimation)是在概率论中用来估计未知的密度函数，属于非参数检验方法之一。通过核密度估计图可以比较直观的看出数据样本本身的分布特征。

seaborn.kdeplot(data,data2=None,shade=False,vertical=False,kernel='gau',bw='scott',gridsize=100,cut=3,clip=None,legend=True,cumulative=False,shade_lowest=True,cbar=False, cbar_ax=None, cbar_kws=None, ax=None, *kwargs)

具体示例如下：

#核密度估计图示例

import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif']=['SimHei']#用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False#用来正常显示负号

sns.set_style("darkgrid",{'font.sans-serif':['simhei','Arial']}) #设置主题
inputfile = 'D:/ProgramData/Anaconda2/envs/python36/project/project02/data/model_data_jiangwei_train.csv'
train = pd.read_csv(inputfile)

fig, axes = plt.subplots(2,2)
ax0=sns.kdeplot(train['ONLINE_TIME'][train['IS_CJ']==1],color='#C74F54',label="已拆机",ax=axes[0,0])
ax0=sns.kdeplot(train['ONLINE_TIME'][train['IS_CJ']==0],color='#8CB9D0',shade=True,label="未拆机",ax=axes[0,0])
axes[0,0].set_title('ONLINE_TIME')
ax1=sns.kdeplot(train['AVG_MOU'][train['IS_CJ']==1],color='r',label="已拆机",ax=axes[0,1])
ax1=sns.kdeplot(train['AVG_MOU'][train['IS_CJ']==0],color='b',shade=True,label="未拆机",ax=axes[0,1])
axes[0,1].set_title('AVG_MOU')
ax1=sns.kdeplot(train['FEE_Trend'][train['IS_CJ']==1],color='r',label="已拆机",ax=axes[1,0])
ax1=sns.kdeplot(train['FEE_Trend'][train['IS_CJ']==0],color='b',shade=True,label="未拆机",ax=axes[1,0])
axes[1,0].set_title('FEE_Trend')
ax1=sns.kdeplot(train['FEE_Fluctuation'][train['IS_CJ']==1],color='r',label="已拆机",ax=axes[1,1])
ax1=sns.kdeplot(train['FEE_Fluctuation'][train['IS_CJ']==0],color='b',shade=True,label="未拆机",ax=axes[1,1])
axes[1,1].set_title('FEE_Fluctuation')
plt.show()

sns.lmplot(x="MOU_COUNT_Sum", y="MOU_Sum",hue="IS_CJ",data=train)
plt.show()

输出结果如下： 可以看出，已拆机用户的在线时长集中子啊0-10月的概率更高，户均通话时长集中在0，收入几乎无波动

3. 数据模型建立与评估

3.1  特征选择

本案例数据共有43个字段，选用不同字段训练出来的模型是不同的，特征选择主要有两个功能：

• 减少特征数量、降维可以使模型泛化能力更强，减少过拟合
• 增强对特征和特征值之间的理解

几种常用的特征选择方法如下：

1）单变量特征选择 

单变量特征选择能够对每一个特征进行测试，衡量该特征和响应变量之间的关系，根据得分扔掉不好的特征。对于回归和分类问题可以采用卡方检验等方式对特征进行测试。皮尔森相关系数是一种最简单的，能帮助理解特征和响应变量之间关系的方法，该方法衡量的是变量之间的线性相关性，结果的取值区间为[-1，1]，-1表示完全的负相关(这个变量下降，那个就会上升)，+1表示完全的正相关，0表示没有线性相关。

注：Pearson相关系数要求两个连续性变量符合正态分布,不服从正态分布的变量、分类或等级变量之间的关联性可采用Spearman秩相关系数，也称为等级相关系数

2) 基于学习模型的特征排序

假如某个特征和响应变量之间的关系是非线性的，可以用基于树的方法（决策树、随机森林）、或者扩展的线性模型等。基于树的方法比较易于使用，因为他们对非线性关系的建模比较好，并且不需要太多的调试。但要注意过拟合问题，因此树的深度最好不要太大，再就是运用交叉验证。

在 波士顿房价数据集 上使用sklearn的 随机森林回归 给出一个单变量选择的例子：

from sklearn.cross_validation import cross_val_score, ShuffleSplit
from sklearn.datasets import load_boston
from sklearn.ensemble import RandomForestRegressor
 
#Load boston housing dataset as an example
boston = load_boston()
X = boston["data"]
Y = boston["target"]
names = boston["feature_names"]
 
rf = RandomForestRegressor(n_estimators=20, max_depth=4)
scores = []
for i in range(X.shape[1]):
     score = cross_val_score(rf, X[:, i:i+1], Y, scoring="r2",
                              cv=ShuffleSplit(len(X), 3, .3))
     scores.append((round(np.mean(score), 3), names[i]))
print sorted(scores, reverse=True)

3) 线性模型

 

通过回归模型的系数来选择特征。越是重要的特征在模型中对应的系数就会越大，而跟输出变量越是无关的特征对应的系数就会越接近于0。在噪音不多的数据上，或者是数据量远远大于特征数的数据上，如果特征之间相对来说是比较独立的，那么即便是运用最简单的线性回归模型也一样能取得非常好的效果。

import pandas as pd
import numpy as np
from sklearn.utils import shuffle

inputfile1 = 'D:/ProgramData/Anaconda2/envs/python36/project/project02/data/model_data_jiangwei_train.csv'
data = pd.read_csv(inputfile1)
# data = shuffle(data)

from sklearn.linear_model import LogisticRegression as LR
from sklearn.linear_model import RandomizedLogisticRegression as RLR
x=data.iloc[:,:42].as_matrix()
y=data.iloc[:,42].as_matrix()
#随机逻辑回归模型筛选特征
rlr=RLR(selection_threshold=0.5)
rlr.fit(x,y)
rlr.get_support()
print(u'通过随机逻辑回归模型筛选特征结束。')
print(u'有效特征为：%s'%','.join(data.drop('IS_CJ',axis=1).columns[rlr.get_support()]))
x=data[data.drop('IS_CJ',axis=1).columns[rlr.get_support()]].as_matrix()
lr=LR()
lr.fit(x,y)
print(u'逻辑回归模型训练结束。')
print(u'模型的平均正确率为：%s'%lr.score(x,y))

#随机森林筛选特征
from sklearn.ensemble import RandomForestClassifier

3.2  LM神经网络模型

人工神经网络（Artificial Neural Networks，ANN）是模拟生物神经网络进行信息处理的一种数学模型。常用的分类与预测的人工神经网络算法有BP神经网络和LM神经网络。BP神经网络是一种按误差逆向传播算法训练的多层前馈网络，LM神经网络是基于梯度下降法和牛顿法结合的多层前馈网络，LM神经网络迭代次数少，收敛速度快和精确度高，故文案例选用LM神经网络进行用户分类。

设定LM神经网络的输入节点数为10，激活函数为tanh，输出节点数为1，激活函数为sigmoid，实验后选取隐含层数为6，输入节点数分别为40、40、30、30、20、20，输出节点数分别为40、30、30、20、20、10，激活函数为relu。

训练模型脚本如下：

from __future__ import print_function
import pandas as pd
import pandas as np
import matplotlib.pyplot as plt
from keras.models import Sequential
from keras.layers.core import Dense, Dropout, Activation
from sklearn.metrics import accuracy_score
from sklearn.metrics import roc_curve #导入ROC曲线函数

inputfile1 = 'D:/ProgramData/Anaconda2/envs/python36/project/project02/data/model_data_train_2.xlsx'
inputfile2 = 'D:/ProgramData/Anaconda2/envs/python36/project/project02/data/model_data_test_2.xlsx'

data_train = pd.read_excel(inputfile1)
data_train[u'FEE_Trend'] = (data_train[u'FEE_Trend'] - data_train[u'FEE_Trend'].mean())/(data_train[u'FEE_Trend'].std())
data_train[u'FEE_Sum'] = (data_train[u'FEE_Sum'] - data_train[u'FEE_Sum'].mean())/(data_train[u'FEE_Sum'].std())
data_train[u'STM_DATA_Sum'] = (data_train[u'STM_DATA_Sum'] - data_train[u'STM_DATA_Sum'].mean())/(data_train[u'STM_DATA_Sum'].std())
data_train[u'STM_DATA_Fluctuation'] = (data_train[u'STM_DATA_Fluctuation'] - data_train[u'STM_DATA_Fluctuation'].mean())/(data_train[u'STM_DATA_Fluctuation'].std())

y_train = data_train.iloc[:, 2].as_matrix()
x_train = data_train.iloc[:, 3:].as_matrix()
x_train = round(pd.DataFrame(x_train), 2).values.tolist()

data_test = pd.read_excel(inputfile2)
data_test[u'FEE_Trend'] = (data_test[u'FEE_Trend'] - data_test[u'FEE_Trend'].mean())/(data_test[u'FEE_Trend'].std())
data_test[u'FEE_Sum'] = (data_test[u'FEE_Sum'] - data_test[u'FEE_Sum'].mean())/(data_test[u'FEE_Sum'].std())
data_test[u'STM_DATA_Sum'] = (data_test[u'STM_DATA_Sum'] - data_test[u'STM_DATA_Sum'].mean())/(data_test[u'STM_DATA_Sum'].std())
data_test[u'STM_DATA_Fluctuation'] = (data_test[u'STM_DATA_Fluctuation'] - data_test[u'STM_DATA_Fluctuation'].mean())/(data_test[u'STM_DATA_Fluctuation'].std())

y_test = data_test.iloc[:, 2].as_matrix()
x_test = data_test.iloc[:, 3:].as_matrix()
x_test = round(pd.DataFrame(x_test), 2).values.tolist()

model = Sequential() #建立模型
model.add(Dense(input_dim = 10, units = 40))
model.add(Activation('tanh'))
model.add(Dense(input_dim = 40, units = 40))
model.add(Activation('relu'))
model.add(Dropout(0.2)) #随机忽略20%神经元，防止训练数据过于拟合
model.add(Dense(input_dim = 40, units = 30))
model.add(Activation('relu'))
model.add(Dropout(0.2))
model.add(Dense(input_dim = 30, units = 30))
model.add(Activation('relu'))
model.add(Dropout(0.2))
model.add(Dense(input_dim = 30, units = 20))
model.add(Activation('relu'))
model.add(Dropout(0.2))
model.add(Dense(input_dim = 20, units = 20))
model.add(Activation('relu'))
model.add(Dense(input_dim = 20, units = 10))
model.add(Activation('relu'))
model.add(Dense(input_dim = 10, units = 1))
model.add(Activation('sigmoid'))
model.compile(loss='mean_squared_error', optimizer='adam')
model.fit(x_train, y_train, epochs = 500, batch_size = 200)
model.save('D:/ProgramData/Anaconda2/envs/python36/project/project02/tmp/neural_net0.model')

def cm_plot(y, yp):
    from sklearn.metrics import confusion_matrix  # 导入混淆矩阵函数
    cm = confusion_matrix(y, yp)  # 混淆矩阵
    import matplotlib.pyplot as plt  # 导入作图库
    plt.matshow(cm, cmap=plt.cm.Greens)  # 画混淆矩阵图
    plt.colorbar()  # 颜色标签
    for x in range(len(cm)):  # 数据标签
        for y in range(len(cm)):
            plt.annotate(cm[x, y], xy=(x, y), horizontalalignment='center', verticalalignment='center')
    plt.ylabel('Predicted label')  # 坐标轴标签
    plt.xlabel('True label')  # 坐标轴标签
    return plt
yp = model.predict_classes(x_train).reshape(len(y_train))
print(accuracy_score(y_train, yp)) #计算模型准确率
cm_plot(y_test,yp).show()

predict_result = model.predict(x_test).reshape(len(y_test))
fpr, tpr, thresholds = roc_curve(y_test, predict_result, pos_label=1)
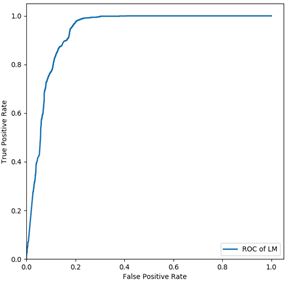
plt.plot(fpr, tpr, linewidth=2, label = 'ROC of LM') #作出ROC曲线
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.ylim(0,1.05)
plt.xlim(0,1.05)
plt.legend(loc=4)
plt.show()

 训练模型混淆矩阵结果：

通过混淆矩阵可算得分类准确率为：

（109512+12455）/（109512+12455+6835+3281）= 92.34%

流失覆盖率为：

12455/（12455+3281）= 79.15%

模型评估：

 

3.3  CART决策树模型

决策树在分类、预测、规则提取等领域有着广泛的应用。决策树是一树状结构，它的每一个叶节点对应着一个分类，非叶节点对应着某个属性的划分，根据样本在该属性上的不同取值将其划分成若干个子集。构造决策树的核心问题是在每一步如何选择适当的属性对样本做拆分。

常用的决策树算法见下表：

训练模型脚本如下：

import pandas as pd
from sklearn.tree import DecisionTreeClassifier #导入决策树模型
from sklearn.metrics import confusion_matrix
import matplotlib.pyplot as plt
from sklearn.tree import export_graphviz
from sklearn.externals.six import StringIO
from sklearn.externals import joblib
from sklearn.metrics import classification_report
from sklearn.metrics import roc_curve #导入ROC曲线函数

inputfile1 = 'D:/ProgramData/Anaconda2/envs/python36/project/project02/data/model_data_train_2.xlsx'
inputfile2 = 'D:/ProgramData/Anaconda2/envs/python36/project/project02/data/model_data_test_2.xlsx'
treefile = 'D:/ProgramData/Anaconda2/envs/python36/project/project02/tmp/tree_net1.pkl' #模型输出名字
dotfilr = 'D:/ProgramData/Anaconda2/envs/python36/project/project02/tmp/tree_net1.dot'

data_train = pd.read_excel(inputfile1)
data_train[u'FEE_Trend'] = (data_train[u'FEE_Trend'] - data_train[u'FEE_Trend'].mean())/(data_train[u'FEE_Trend'].std())
data_train[u'FEE_Sum'] = (data_train[u'FEE_Sum'] - data_train[u'FEE_Sum'].mean())/(data_train[u'FEE_Sum'].std())
data_train[u'STM_DATA_Sum'] = (data_train[u'STM_DATA_Sum'] - data_train[u'STM_DATA_Sum'].mean())/(data_train[u'STM_DATA_Sum'].std())
data_train[u'STM_DATA_Fluctuation'] = (data_train[u'STM_DATA_Fluctuation'] - data_train[u'STM_DATA_Fluctuation'].mean())/(data_train[u'STM_DATA_Fluctuation'].std())
y_train = data_train.iloc[:, 2].as_matrix()
x_train = data_train.iloc[:, 3:].as_matrix()
x_train = round(pd.DataFrame(x_train), 2).values.tolist()

data_test = pd.read_excel(inputfile2)
data_test[u'FEE_Trend'] = (data_test[u'FEE_Trend'] - data_test[u'FEE_Trend'].mean())/(data_test[u'FEE_Trend'].std())
data_test[u'FEE_Sum'] = (data_test[u'FEE_Sum'] - data_test[u'FEE_Sum'].mean())/(data_test[u'FEE_Sum'].std())
data_test[u'STM_DATA_Sum'] = (data_test[u'STM_DATA_Sum'] - data_test[u'STM_DATA_Sum'].mean())/(data_test[u'STM_DATA_Sum'].std())
data_test[u'STM_DATA_Fluctuation'] = (data_test[u'STM_DATA_Fluctuation'] - data_test[u'STM_DATA_Fluctuation'].mean())/(data_test[u'STM_DATA_Fluctuation'].std())
y_test = data_test.iloc[:, 2].as_matrix()
x_test = data_test.iloc[:, 3:].as_matrix()
x_test = round(pd.DataFrame(x_test), 2).values.tolist()

tree = DecisionTreeClassifier() #建立决策树模型
tree.fit(x_train,y_train) #训练
joblib.dump(tree, treefile)
result = tree.predict(x_test)
x=data_train.iloc[:,3:].astype(int)
with open(dotfilr,'w') as f:
    f = export_graphviz(tree,feature_names=x.columns,out_file=f)

def cm_plot(y, yp):
    from sklearn.metrics import confusion_matrix  # 导入混淆矩阵函数
    cm = confusion_matrix(y, yp)  # 混淆矩阵
    import matplotlib.pyplot as plt
    plt.matshow(cm, cmap=plt.cm.Greens)
    plt.colorbar()
    for x in range(len(cm)):
        for y in range(len(cm)):
            plt.annotate(cm[x, y], xy=(x, y), horizontalalignment='center', verticalalignment='center')
    plt.ylabel('Predicted label')
    plt.xlabel('True label')
    return plt
yp = tree.predict(x_train).reshape(len(y_train))
print('准确率：',tree.score(x_train,y_train))
print('其他指标：',classification_report(yp,y_train,target_names=['1','0']))
cm_plot(y_train,yp).show()

fpr, tpr, thresholds = roc_curve(y_test, tree.predict_proba(x_test)[:,1], pos_label=1)
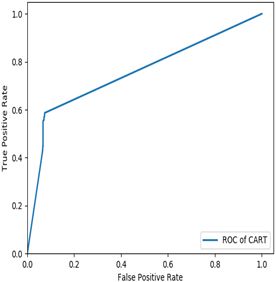
plt.plot(fpr, tpr, linewidth=2, label = 'ROC of CART') #作出ROC曲线
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.ylim(0,1.05)
plt.xlim(0,1.05)
plt.legend(loc=4)
plt.show()

 训练模型混淆矩阵结果：

通过CART决策树 矩阵可算得分类准确率为：

（115695+14991）/（115695+14991+662+745）= 98.93%%

流失覆盖率为：

14991/（14991+745）=95.27%%

模型评估：

对于训练样本， CART决策树分类的模型准确率和流失覆盖率稍微比LM神经网络模型的好，为了进一步评估模型分类的性能，利用测试样本对两个模型进行评价，采用ROC曲线评价方法进行评估，一个良好的分类器对应的ROC曲线应该是尽量靠近左上角，真正越高且假正越小越好。

经过对比发现测试样本下，LM神经网络的ROC曲线比CART决策树的ROC曲线更加靠近单位方形的左上角，LM神经网络ROC曲线下的面积更大。说明CART决策树有过拟合情况存在，LM神经网络模型拟合分类性能相对更好。

本文脚本及数据可从以下地址获得：

https://github.com/shuzhenxie/-