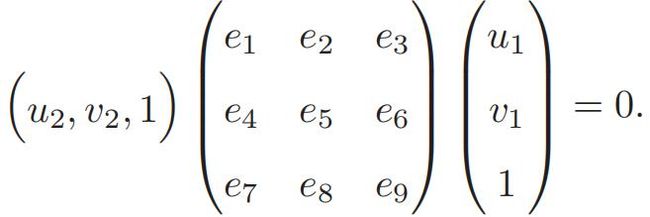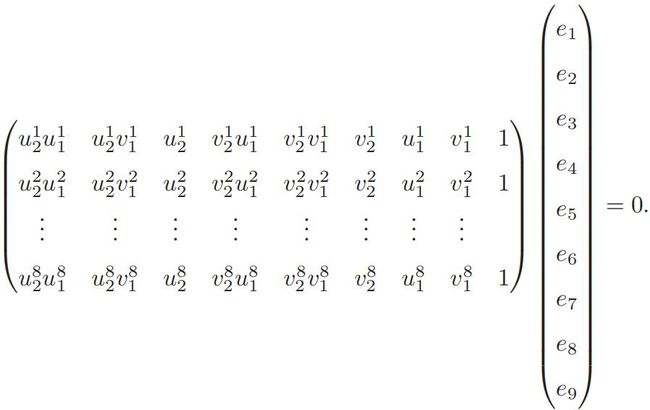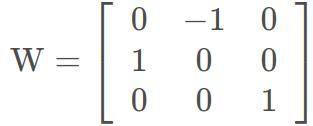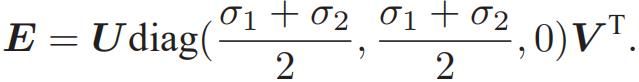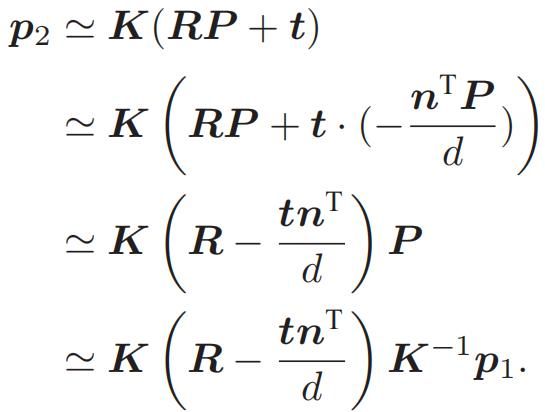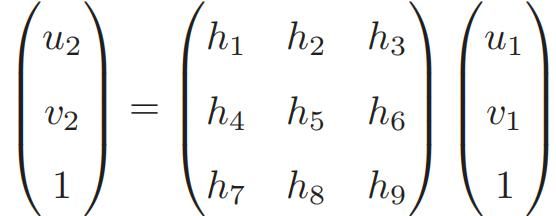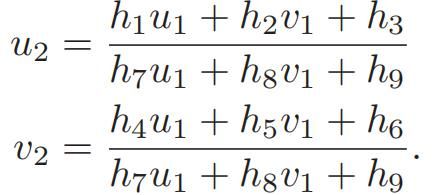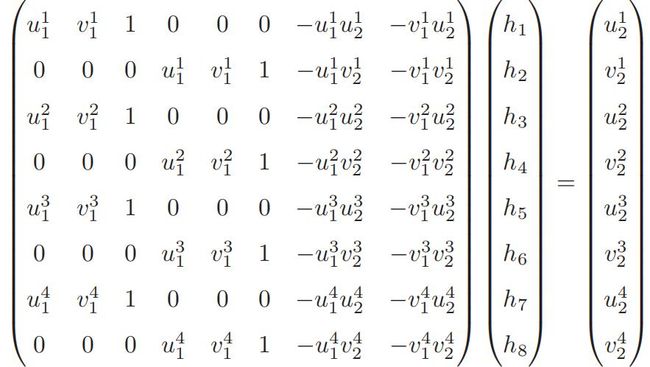对极几何和三角测量

 个人博客：http://www.chenjianqu.com/

原文链接：http://www.chenjianqu.com/show-94.html

在多种应用场景中，我们需要根据运动中相邻的两张图像恢复相机的运动，并计算空间点的深度信息，这个问题可以由对极约束和三角测量解决。

 

对极约束

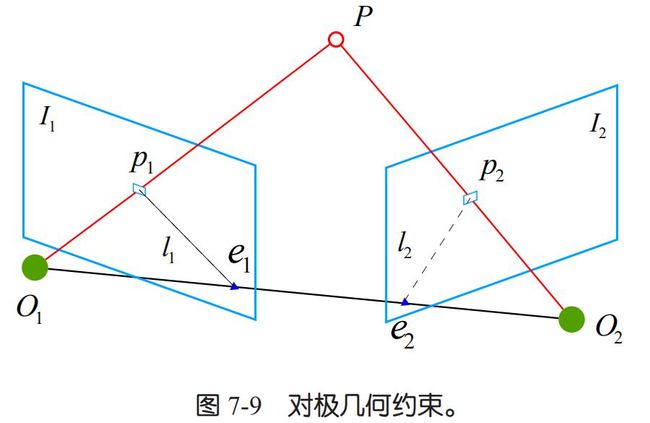
    对极约束可以根据两张图像的匹配的一组特征点计算出相机从第一张图像到第二张的运动。关于计算特征匹配可以使用特征点法、光流法、直接法求解出，比如LK光流跟踪，ORB特征匹配。下面开始介绍对极几何，其示意图如下：

    我们希望求取两帧图像 I1, I2 之间的运动，设第一帧到第二帧的运动为 R, t，两个相机中心分别为 O1, O2，考虑 I1 中有一个特征点 p1，它在 I2 中对应着特征点 p2。连线O1p1和连线O2p2在三维空间相较于点 P，O1O2 P三个点的平面称为极平面(Epipolar plane)。O1O2连线称为基线(Baseline)，基线与像平面I1, I2的交点分别为e1, e2，称为极点(Epipoles)。极平面与两个像平面I1, I2之间的相交线l1, l2为极线(Epipolar line)。

    在第一帧的坐标系下，设 P=[X,Y,Z]，根据相机模型，有 s1p1=KP，s2p2=K(RP+t)，s1,s2是P点在两个坐标系的z轴坐标，K为相机内参矩阵，R, t为第一个坐标系到第二个坐标系的运动。在使用齐次坐标时，一个向量将等于它自身乘上任意的非零常数，这通常用于表达一个投影关系，称为尺度意义下相等(equal up to a scale)。此时，有sp≃p。因此有：p1≃KP，p2≃K(RP+t)。 

    根据相机模型，我们知道 z = 1 平面是归一化平面，归一化坐标 p 和像素坐标 x 的关系为p=Kx ,x=P/s，即x1=K-1p1，x2=K-1p2。将x1 x2代入上式，得 x2≃Rx1+t。两边与平移向量t 做外积：t^ x2≃t^ Rx1+t^ t，t^ t=0，得：t^ x2≃t^ Rx1。等式两侧同时左乘x2T，得 x2T t^ x2≃x2T t^ Rx1。由于t^ x2与x2垂直，故：x2T t^ x2=0 ，得：

    公式一：x2T t^ Rx1 = 0。

    代入p1,p2，而且 x2T=(K-1p2)T = p2T K-T，得：

    公式二：p2T K-T x2T t^ R K-1p1 = 0 。

    记基础矩阵(Fundamental Matrix) F=K-T E K-1 和本质矩阵(Essential Matrix) E=t^ R，最终得：

    对极约束：x2T E x1 = p2T F p1 = 0 。

    于是，相机位姿估计问题变为以下两步：1.根据配对点的像素位置求出E或者F。2.根据E或F求出R,t。下面介绍E的求解方法。

 

本质矩阵的求解

    本质矩阵E=t^ R，是一个3x3的矩阵，后面会证明，奇异值必定是 [σ, σ, 0]T 的形式，这称为本质矩阵的内在性质。由于平移和旋转各有 3 个自由度，故 t^ R 共有 6 个自由度。由于对极约束是等式为零的约束，所以对 E 乘以任意非零常数后，对极约束依然满足，即E在不同尺度下是等价的，故 E 实际上有 5 个自由度。这表明我们最少可以用 5 对点来求解 E。但是，E 的内在性质是一种非线性性质，在估计时会带来麻烦，因此，也可以只考虑它的尺度等价性，使用 8 对点来估计 E——这就是经典的八点法（Eight-point-algorithm）。

    设一对匹配点的归一化坐标为x1=[u1,v1,1]，x2=[u2,v2,1]，对极约束为：x2T E x1=0，矩阵形式为：

    将上式展开，将本质矩阵E展开，e=[e1,e2,e3,e4,e5,e6,e7,e8,e9]T，则对极约束写成e有关的形式：[u2u1,u2v1,u2,v2u1,v2v1,v2,u1,v1,1]*e=0。将8对匹配点放在同一方程组里，得：

    如果 8 对匹配点组成的矩阵满足秩为 8 的条件，那么 E 的各元素就可由上述方程解得。

 

本质矩阵的分解

    得到E之后，由E=t^ R，我们想要通过E恢复得到R,t。

本质矩阵的性质

   证明：一个3×3的矩阵是本质矩阵的充要条件是它的奇异值中有两个相等而第三个是0。 本质矩阵的定义：E=t^ R=SR，其中 t^=S是反对称矩阵。根据反对称矩阵的基本性质，有S=UBUT，其中B是diag(a1Z, a2Z, ..., amZ, 0, ..., 0)的分块对角阵，Z=[[0,1],[-1,0]]。反对称矩阵的特征矢量都是纯虚数并且奇数阶的反对称矩阵必是奇异的。则可以将S写成S=kUZUT，其中Z为：

    Z可以写成Z=diag(1,1,0)W，其中W为：

    因此E矩阵可以分解为：E = SR = U diag(1,1,0) (WUTR)。由此证明E的奇异值必定是 [σ, σ, 0]T 的形式。

SVD分解

    上面说过，S=kUZUT，在相差一个常数因子的情况下S=UZUT。设旋转矩阵R的SVD分解为R=UXVT。则有：

    U diag(1,1,0) VT= E = SR = (UZUT)(UXVT) = U(ZX)VT

    即ZX=diag(1,1,0)，因此X=W或X=WT。因此：

    E的SVD两种分解形式为：E=SR，S=UZUT，R=UWVT或R=UWTVT

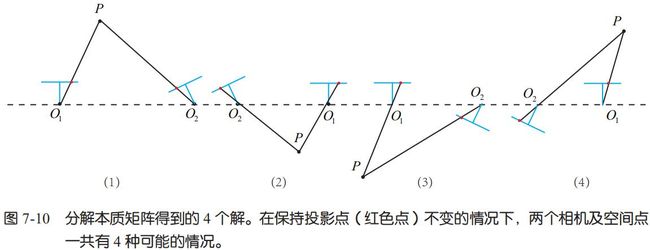
    又因为St=0，|t|=1，因此t=U(0,0,1)T=u3，即矩阵U的最后一列。因为t的符号不确定，R也有两种情况，故分解有四种情况：

    变换矩阵 T = [UWVT∣+u3] or [UWVT∣−u3]or[UWTVT∣+u3] or [UWTVT∣−u3]

    因此，从 E 分解到 t, R 时，一共存在 4 个可能的解。    

    上面只有第一种解中 P 在两个相机中都具有正的深度。因此，只要把任意一点代入 4 种解中，检测该点在两个相机下的深度，就可以确定哪个解是正确的了。

    根据线性方程解出的 E，可能不满足 E 的内在性质：奇异值为 (σ, σ, 0)。通常的做法是，对八点法求得的 E 进行 SVD 分解后，会得到奇异值矩阵 Σ = diag(σ1, σ2, σ3)，设 σ1 ⩾ σ2 ⩾ σ3，取：

    这相当于是把求出来的矩阵投影到了 E 所在的流形上。更简单的做法是将奇异值矩阵取成diag(1, 1, 0)，因为 E 具有尺度等价性，所以这样做也是合理的。

 

单应矩阵的求解

    单应矩阵(Homography)H，描述了两个平面之间的映射关系。若场景中的特征点都落在同一平面上（比如墙、地面等），则可以通过单应性来进行运动估计。这种情况在无人机携带的俯视相机或扫地机携带的顶视相机中比较常见。

    单应矩阵通常描述处于共同平面上的一些点在两张图像之间的变换关系。考虑在图像 I1, I2有一对匹配好的特征点 p1, p2。这些特征点落在平面 P上，设这个平面满足方程：nT P+d=0，整理得 -nTP/d = 1。由尺度意义下相等，有：

    于是得到了一个直接描述图像坐标 p1, p2 之间的变换，把中间这部分记为 单应矩阵H，于是：p2≃Hp1，它与旋转、平移及平面的参数有关。与基础矩阵 F 类似，单应矩阵 H 也是一个 3 × 3 的矩阵，求解时的思路也和 F 类似，同样可以先根据匹配点计算 H，然后将它分解以计算旋转和平移。把上式展开，得：

    展开有：

    在实际处理中通常乘以一个非零因子使得h9 = 1（在它取非零值时），得：

    这样一组匹配点对就可以构造出两项约束，于是自由度为 8 的单应矩阵可以通过 4 对匹配特征点算出（注意，这些特征点不能有三点共线的情况），即求解以下的线性方程组（当 h9 = 0 时，右侧为零）：

    这种做法把 H 矩阵看成了向量，通过解该向量的线性方程来恢复H，又称直接线性变换法(Direct Linear Transform)。与本质矩阵相似，求出单应矩阵以后需要对其进行分解，才可以得到相应的旋转矩阵 R 和平移向量 t。分解的方法包括数值法与解析法。单应矩阵的分解同样会返回 4 组旋转矩阵与平移向量，并且同时可以计算出它们分别对应的场景点所在平面的法向量。如果已知成像的地图点的深度全为正值（即在相机前方），则又可以排除两组解。最后仅剩两组解，这时需要通过更多的先验信息进行判断。

    单应性在 SLAM 中具有重要意义。当特征点共面或者相机发生纯旋转时，基础矩阵的自由度下降，这就出现了所谓的退化（degenerate）。现实中的数据总包含一些噪声，这时候如果继续使用八点法求解基础矩阵，基础矩阵多余出来的自由度将会主要由噪声决定。为了能够避免退化现象造成的影响，通常我们会同时估计基础矩阵 F 和单应矩阵 H，选择重投影误差比较小的那个作为最终的运动估计矩阵。

 

三角测量

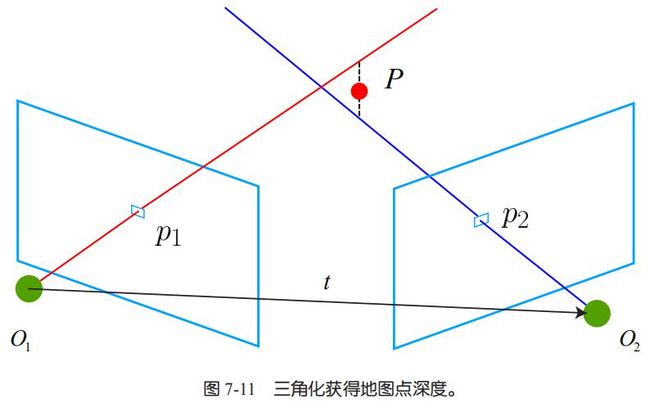
    在单目 SLAM 中，仅通过单张图像无法获得像素的深度信息，需要通过三角测量(Triangulation)的方法来估计地图点的深度，如下图：

    三角测量是指，通过在两处观察同一个点的夹角，从而确定该点的距离。考虑图像 I1, I2，以左图为参考，右图的变换矩阵为 T。相机光心为O1, O2。在I1 中有特征点 p1，对应 I1 中有特征点 p2。理论上直线 O1p1 与 O2p2 在场景中会相交于一点 P，该点即两个特征点所对应的地图点在三维场景中的位置。然而由于噪声的影响，这两条直线往往无法相交。因此，可以通过最二小乘法求解。

    设 x1, x2为两个特征点的归一化坐标，那么它们满足：s1x1 = s2Rx2 + t。现在已经知道了 R, t，想要求解的是两个特征点的深度 s1, s2。可以对上式两侧左乘一个 x1^ ，得：

    求解公式：s1 x1^ x1 = 0 = s2 x1^ R x2 + x1^ t。

    上式右侧看成s2的一个方程，可以求得s2。有了s2，就可以求出s1。由于噪声的存在，更常见的做法是求最小二乘解而不是零解。

    纯旋转是无法使用三角测量的，因为对极约束将永远满足。下面是三角测量的矛盾：

    当平移很小时，像素上的不确定性将导致较大的深度不确定性。也就是说，如果特征点运动一个像素 δx，使得视线角变化了一个角度 δθ，那么将测量到深度值有 δd 的变化。从几何关系可以看到，当 t 较大时，δd 将明显变小，这说明平移较大时，在同样的相机分辨率下，三角化测量将更精确。

    因此，要提高三角化的精度，其一是提高特征点的提取精度，也就是提高图像分辨率——但这会导致图像变大，增加计算成本。另一方式是使平移量增大。但是，这会导致图像的外观发生明显的变化，比如箱子原先被挡住的侧面显示出来，又比如反射光发生变化，等等。外观变化会使得特征提取与匹配变得困难。总而言之，再增大平移，会导致匹配失效；而平移太小，则三角化精度不够——这就是三角化的矛盾。

    如果假设特征点服从高斯分布，并且不断地对它进行观测，在信息正确的情况下，我们就能够期望它的方差会不断减小乃至收敛。这就得到了一个滤波器，称为深度滤波器（Depth Filter）。

 

代码实现

    代码用到的OpenCV函数：

1.在图片上显示文字
void cv::putText(
            cv::Mat& img, // 待绘制的图像
            const string& text, // 待绘制的文字
            cv::Point origin, // 文本框的左下角
            int fontFace, // 字体 (如cv::FONT_HERSHEY_PLAIN)
            double fontScale, // 尺寸因子，值越大文字越大
            cv::Scalar color, // 线条的颜色（RGB）
            int thickness = 1, // 线条宽度
            int lineType = 8, // 线型（4邻域或8邻域，默认8邻域）
            bool bottomLeftOrigin = false // true='origin at lower left'
);


2.本质矩阵求解函数
Mat findEssentialMat(
    InputArray points1, //第一帧中特征匹配点，
    InputArray points2, //第二帧中特征匹配点
    double focal = 1.0, //相机焦距
    Point2d pp = Point2d(0, 0), //相机主点
    int method = RANSAC, //这里采用RANSAC算法计算本质矩阵，还有LMEDS算法
    double prob = 0.999,
    double threshold = 1.0, 
    OutputArray mask = noArray() 
);


3.从本质矩阵中恢复旋转和平移信息.
int recoverPose( 
    InputArray E, //本质矩阵
    InputArray points1, //第一帧中特征匹配点，
    InputArray points2, //第二帧中特征匹配点，
    OutputArray R, //旋转矩阵
    OutputArray t, //平移向量
    double focal = 1.0, //相机焦距
    Point2d pp = Point2d(0, 0),  //相机主点
    InputOutputArray mask = noArray() 
);


4.三角测量函数
void triangulatePoints( 
    InputArray projMatr1, //从源坐标系到第一张图片的变换矩阵，在这里以该图像坐标系为原点，因此设为单位阵
    InputArray projMatr2,  //从源坐标系到第而张图片的变换矩阵，这里为第一帧到第二帧的变换矩阵
    InputArray projPoints1, //第一帧中特征匹配点，归一化坐标
    InputArray projPoints2,  //第二帧中特征匹配点，归一化坐标
    OutputArray points4D //测量好的三维点，采取4维齐次坐标的形式
);

    

 

    下面的代码首先匹配ORB特征，然后计算本质矩阵，求解处两帧图像之间的运动，最后采用三角测量计算每个特征点的深度，代码如下：

#include 
#include 

using namespace std;
using namespace cv;

//特征匹配
void find_feature_matches(
  const Mat &img_1, const Mat &img_2,
  std::vector &keypoints_1,
  std::vector &keypoints_2,
  std::vector &matches);

//运动估计
void pose_estimation_2d2d(
  const std::vector &keypoints_1,
  const std::vector &keypoints_2,
  const std::vector &matches,
  Mat &R, Mat &t);
  
 //三角测量
void triangulation(
  const vector &keypoint_1,
  const vector &keypoint_2,
  const std::vector &matches,
  const Mat &R, const Mat &t,
  vector &points
);

//根据深度返回不同的颜色
inline cv::Scalar get_color(float depth) {
  float up_th = 50, low_th = 10, th_range = up_th - low_th;
  if (depth > up_th) depth = up_th;
  if (depth < low_th) depth = low_th;
  return cv::Scalar(255 * depth / th_range, 255 * depth / th_range, 255 * depth / th_range);
}

// 像素坐标转相机归一化坐标
Point2f pixel2cam(const Point2d &p, const Mat &K);

int main(int argc, char **argv) 
{
  //读取图像
  Mat img_1 = imread("1.png", CV_LOAD_IMAGE_COLOR);
  Mat img_2 = imread("2.png", CV_LOAD_IMAGE_COLOR);
  
  //特征匹配
  vector keypoints_1, keypoints_2;
  vector matches;
  find_feature_matches(img_1, img_2, keypoints_1, keypoints_2, matches);
  
  cout << "一共找到了" << matches.size() << "组匹配点" << endl;
  
  //估计两张图像间运动
  Mat R, t;
  pose_estimation_2d2d(keypoints_1, keypoints_2, matches, R, t);
  
  //三角化
  vector points;
  triangulation(keypoints_1, keypoints_2, matches, R, t, points);
  
  //验证三角化点与特征点的重投影关系
  Mat K = (Mat_(3, 3) << 520.9, 0, 325.1, 0, 521.0, 249.7, 0, 0, 1);
  Mat img1_plot = img_1.clone();
  Mat img2_plot = img_2.clone();
  for (int i = 0; i < matches.size(); i++) {
    // 第一个图
    float depth1 = points[i].z;
    cout << "depth: " << depth1 << endl;
    Point2d pt1_cam = pixel2cam(keypoints_1[matches[i].queryIdx].pt, K);
    cv::circle(img1_plot, keypoints_1[matches[i].queryIdx].pt, 2, get_color(depth1), 2);
    
    if(i%5==0)
        cv::putText(img1_plot,to_string(int(depth1)), keypoints_1[matches[i].queryIdx].pt, cv::FONT_HERSHEY_PLAIN, 1,(255,255,255), 1);

    // 第二个图
    Mat pt2_trans = R * (Mat_(3, 1) << points[i].x, points[i].y, points[i].z) + t;
    float depth2 = pt2_trans.at(2, 0);
    
    cv::circle(img2_plot, keypoints_2[matches[i].trainIdx].pt, 2, get_color(depth2), 2);
  }
  cv::imshow("img 1", img1_plot);
  cv::imshow("img 2", img2_plot);
  cv::waitKey();
  return 0;
}


void find_feature_matches(const Mat &img_1, const Mat &img_2,
                          std::vector &keypoints_1,
                          std::vector &keypoints_2,
                          std::vector &matches) {
  //-- 初始化
  Mat descriptors_1, descriptors_2;
  Ptr detector = ORB::create();
  Ptr descriptor = ORB::create();
  Ptr matcher = DescriptorMatcher::create("BruteForce-Hamming");
  //-- 第一步:检测 Oriented FAST 角点位置
  detector->detect(img_1, keypoints_1);
  detector->detect(img_2, keypoints_2);
  //-- 第二步:根据角点位置计算 BRIEF 描述子
  descriptor->compute(img_1, keypoints_1, descriptors_1);
  descriptor->compute(img_2, keypoints_2, descriptors_2);
  //-- 第三步:对两幅图像中的BRIEF描述子进行匹配，使用 Hamming 距离
  vector match;
  matcher->match(descriptors_1, descriptors_2, match);
  //-- 第四步:匹配点对筛选
  double min_dist = 10000, max_dist = 0;
  //找出所有匹配之间的最小距离和最大距离, 即是最相似的和最不相似的两组点之间的距离
  for (int i = 0; i < descriptors_1.rows; i++) {
    double dist = match[i].distance;
    if (dist < min_dist) min_dist = dist;
    if (dist > max_dist) max_dist = dist;
  }
  //当描述子之间的距离大于两倍的最小距离时,即认为匹配有误.但有时候最小距离会非常小,设置一个经验值30作为下限.
  for (int i = 0; i < descriptors_1.rows; i++)
    if (match[i].distance <= max(2 * min_dist, 30.0))
      matches.push_back(match[i]);
}



void pose_estimation_2d2d(const std::vector &keypoints_1,
  const std::vector &keypoints_2,
  const std::vector &matches,
  Mat &R, 
  Mat &t) 
{
  // 相机内参,TUM Freiburg2
  Mat K = (Mat_(3, 3) << 520.9, 0, 325.1, 0, 521.0, 249.7, 0, 0, 1);

  vector points1,points2;  
  for (int i = 0; i < (int) matches.size(); i++) {
    int index1=matches[i].queryIdx;
    int index2=matches[i].trainIdx;
    points1.push_back(keypoints_1[index1].pt);
    points2.push_back(keypoints_2[index2].pt);
  }
  //计算本质矩阵
  Point2d principal_point(325.1, 249.7);        //相机主点, TUM dataset标定值
  int focal_length = 521;            //相机焦距, TUM dataset标定值
  Mat essential_matrix;
  essential_matrix = findEssentialMat(points1, points2, focal_length, principal_point);
  //-- 从本质矩阵中恢复旋转和平移信息.
  recoverPose(essential_matrix, points1, points2, R, t, focal_length, principal_point);
}


void triangulation(
  const vector &keypoint_1,
  const vector &keypoint_2,
  const std::vector &matches,
  const Mat &R, const Mat &t,
  vector &points) 
{
    
  Mat T1 = (Mat_(3, 4) <<
    1, 0, 0, 0,
    0, 1, 0, 0,
    0, 0, 1, 0);
  Mat T2 = (Mat_(3, 4) <<
    R.at(0, 0), R.at(0, 1), R.at(0, 2), t.at(0, 0),
    R.at(1, 0), R.at(1, 1), R.at(1, 2), t.at(1, 0),
    R.at(2, 0), R.at(2, 1), R.at(2, 2), t.at(2, 0)
  );
  Mat K = (Mat_(3, 3) << 520.9, 0, 325.1, 0, 521.0, 249.7, 0, 0, 1);
  
  vector pts_1, pts_2;
  for (DMatch m:matches) {
    pts_1.push_back(pixel2cam(keypoint_1[m.queryIdx].pt, K));// 将像素坐标转换至相机坐标
    pts_2.push_back(pixel2cam(keypoint_2[m.trainIdx].pt, K));
  }
  Mat pts_4d;
  cv::triangulatePoints(T1, T2, pts_1, pts_2, pts_4d);
  // 转换成非齐次坐标
  for (int i = 0; i < pts_4d.cols; i++) {
    Mat x = pts_4d.col(i);
    x /= x.at(3, 0); // 归一化
    Point3d p(
      x.at(0, 0),
      x.at(1, 0),
      x.at(2, 0)
    );
    points.push_back(p);
  }
}


Point2f pixel2cam(const Point2d &p, const Mat &K) {
  return Point2f
    (
      (p.x - K.at(0, 2)) / K.at(0, 0),
      (p.y - K.at(1, 2)) / K.at(1, 1)
    );
}

 

 

 

 

参考文献

[0]高翔.视觉SLAM14讲

[1]Jichao_Peng.多视图几何总结——从本质矩阵恢复摄像机矩阵.https://blog.csdn.net/weixin_44580210/article/details/90344511.  2019-05-20