WaWa的奇妙冒险（第四周集训自闭现场）

（一）wlacm例题记录

A-FBI树 （水题，位运算）

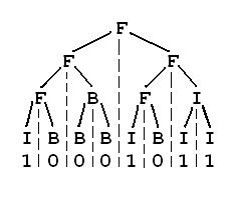
我们可以把由“0”和“1”组成的字符串分为三类：全“0”串称为B串，全“1”串称为I串，既含“0”又含“1”的串则称为F串。
FBI树是一种二叉树[ 二叉树：二叉树是结点的有限集合，这个集合或为空集，或由一个根结点和两棵不相交的二叉树组成。这两棵不相交的二叉树分别称为这个根结点的左子树和右子树。]，它的结点类型也包括F结点，B结点和I结点三种。由一个长度为2N的“01”串S可以构造出一棵FBI树T，递归的构造方法如下：
T的根结点为R，其类型与串S的类型相同；
若串S的长度大于1，将串S从中间分开，分为等长的左右子串S1和S2；由左子串S1构造R的左子树T1，由右子串S2构造R的右子树T2。
现在给定一个长度为2N的“01”串，请用上述构造方法构造出一棵FBI树，并输出它的后序遍历。

Input

输入的第一行是一个整数N（0 <= N <= 10），第二行是一个长度为2^N的“01”串。

Output

输出包括一行，这一行只包含一个字符串，即FBI树的后序遍历序列。

Sample Input

3
10001011

Sample Output

IBFBBBFIBFIIIFF

理解

	很简单的建树题，简单考了一下建树的方式而已，拿出来记录一下也是因为这题我用了一下位运算，就当熟悉一下

AC代码

#include 
using namespace std;
 
string k,post;
struct node{
    char val;
    node *left,*right;
    node(int val = 0,node *left = NULL,node *right = NULL):val(val),left(left),right(right){}
};
  
void buildtree(int l,int r,node* &root){
    int sum = 0;
    for(int i = l;i < r;i++){
        sum = sum*2 + k[i] - '0';  ##　分割输入的字符串
    }
     
    if(!sum) root = new node('B');
    else if(sum == (1 << (r - l)) - 1) root = new node('I');  ##  位运算判断是否全1，==可以写成&
    else root = new node('F');
 
    if(l == r - 1) return;
    buildtree(l,(l+r)/2,root -> left);  ##  二分的思想
    buildtree((l+r)/2,r,root -> right);
}
  
void postorder(node *root){
    if(root != NULL){
        postorder(root -> left);
        postorder(root -> right);
        if(root -> val != '.') post += root -> val;　　##　后序遍历得到路径
    }
    return;
}
  
int main()
{
    int n;
    cin >> n;
    n = 1 << n;
    cin >> k;
     
    node *root;
    buildtree(0,n,root);
    post = "";
    postorder(root);
    cout << post << endl;
    return 0;
}

B-查找二叉树 （模拟先序遍历）

已知一棵二叉树用邻接表结构存储，中序查找二叉树中值为x的结点，并指出是第几个结点。

Input

第一行n为二叉树的结点个树，n<=100；第二行x表示要查找的结点的值；以下第一列数据是各结点的值，第二列数据是左儿子结点编号，第三列数据是右儿子结点编号。

Output

输出要查找的结点数目。

Sample Input

7
15
5 2 3
12 4 5
10 0 0
29 0 0
15 6 7
8 0 0
23 0 0

Sample Output

4

理解

	这题还是很有趣的，首先你要理解先序查找的方式，他永远是左中右的遍历方式，因此我们可以把问题细化
	（１）往左走，走的路上不会计数，因为先到最左，返程计数
	（２）往右走，他必然先检查左子树，返回（１）的思路，左子树走完，或者没有之后，自身计数，再想右走
	根据这两点就能写出代码了，但刚开始确实卡了挺久，没想清楚，可以写的时候自己调整递归出口的位置

AC代码

#include 
using namespace std;
 
int m,ans = 0;
struct node{
    int val;
    int left,right;
} P[105];  ##  数组建树，这题需要内存空间不大
 
void dfs(int x){
    if(P[x].left) dfs(P[x].left);　##  往左走先卡死，到底计数
    ans++;
     
    if(P[x].val == m){  ##  递归出口要放中间，之前习惯性写开头错了
        cout << ans << endl;
        exit(0);  ##  直接结束程序，避免不必要的递归
    }
     
    if(P[x].right) dfs(P[x].right);  ##  往右走如果没有左子树卡死，直接计数
     
    return;
}
 
int main()
{
    memset(P,0,sizeof(P));
    ans = 0;
    int n;
    cin >> n >> m;
    for(int i = 1;i <= n;i++){
        cin >> P[i].val >> P[i].left >> P[i].right;
    }
    dfs(1);
    return 0;
}

C-删数问题 （栈的运用）

输入一个高精度的正整数N，去掉其中任意S个数字后剩下的数字按原左右次序组成一个新的正整数。编程对给定的N和S，寻找一种方案使得剩下的数字组成的新数最小。
输出新的正整数。（N不超过240位）输入数据均不需判错。

Input

n
s

Output

最后剩下的最小数。

Sample Input

175438
4

Sample Output

13

理解

	这题刚开始以为去掉最大数就好，结果发现错了。
	后面用了暴力模拟的方式substr找规律，发现只要找到第一个非下降序列的末尾，删掉即可
	不过emm 要注意先导0的情况，代码也是写的比较差

AC代码

#include 
using namespace std;
  
int main()
{
    string s;
    int n,k = -1;
    cin >> s >> n;
    for(int i = 0;i < s.size();i++){  ##  找到第一个非0，这里推荐改成upper_bound，当时写的时候比较菜
        if(s[i] != '0'){
            k = i;
            break;
        }
    }
    if(k == -1){  ##  如果全是0，无论怎么删都是0，直接输出0即可
        cout << 0 << endl;
        return 0;
    }
    else s = s.substr(k,s.size() - k);  ##  不然的话，去掉先导0
      
    for(int i = 0;i < n;i++){
        int j;
        for(j = 0;j < s.size() - 1;j++){
            if(s[j] > s[j + 1]) break;
        }
        s = s.substr(0,j) + s.substr(j + 1,s.size() - j - 1);  ##  很简单的删数操作，可以而erase来着，个人substr用的比较习惯
    }
     
    k = -1;
    for(int i = 0;i < s.size();i++){  ##  找删完之后的非0位置
        if(s[i] != '0'){
            k = i;
            break;
        }
    }
     
    if(k != -1) s = s.substr(k,s.size() - k);  ##  删完后不是0就去前导0
    else s = "";  ##  如果值为0就定位空串
    if(s != "") cout << s << endl;  ##  根据是否为空串看它该输出啥（这里当时思路不清，写复杂了，直接-1判断即可）
    else cout << 0 << endl;
    return 0;
}

D-导弹拦截 （贪心）

某国为了防御敌国的导弹袭击，开发出一种导弹拦截系统，但是这种拦截系统有一个缺陷：虽然它的第一发炮弹能够到达任意的高度，但是以后每一发炮弹都不能高于前一发的高度。某天，雷达捕捉到敌国的导弹来袭，由于该系统还在试用阶段。所以一套系统有可能不能拦截所有的导弹。

   输入导弹依次飞来的高度（雷达给出的高度不大于30000的正整数）。计算要拦截所有导弹最小需要配备多少套这种导弹拦截系统。

Input

n颗依次飞来的高度（1≤n≤1000）

Output

要拦截所有导弹最小配备的系统数k

Sample Input

389 207 155 300 299 170 158 65

Sample Output

2

理解

	刚开始想起来很复杂，后来写代码的时候发现，其实就是对于每个新来的的导弹都应该判断是否能被老的系统接下导弹，如果可以，优先挑位置低的系统
	接导弹，刚开始还写了一个排序，每次接完导弹排个序，后来发现，其实按顺序遍历的过程中，他已经起到了一个排序的作用。

AC代码

#include 
using namespace std;
    
int main()
{
    int a[1005],k = 0,ans = 0;
    int b[1005] = {0};
    while(cin >> a[k++]);
    k--;
       
    for(int i = 0;i < k;i++){
        bool f = 1;
        for(int j = 1;j <= ans;j++){  ##  看现有的系统能不能拦截导弹
            if(a[i] <= b[j]){
                f = 0;
                b[j] = a[i];  ##  如果能，就更行该系统的最低高度
                break;
            }
        }
        if(f){  ##  如果不能，新建一个系统
            ans++;
            b[ans] = a[i];
        }
    }
    cout << ans << endl;
    return 0;
}

E-整数区间 （贪心）

请编程完成以下任务：

1.读取闭区间的个数及它们的描述； 　　
2.找到一个含元素个数最少的集合,使得对于每一个区间,都至少有一个整数属于该集合，输出该集合的元素个数。

Input

首行包括区间的数目n,1<=n<=10000,接下来的n行,每行包括两个整数a,b,被一空格隔开,0<=a<=b<=10000,它们是某一个区间的开始值和结束值。

Output

第一行集合元素的个数,对于每一个区间都至少有一个整数属于该区间,且集合所包含元素数目最少。

Sample Input

4
3 6
2 4
0 2
4 7

Sample Output

2

理解

	emm 理解起来也挺简单的，就是订钉子的想法，把尽可能多的木板钉在一起，那么我肯定拿第一个木板的末尾作为开始钉的地方
	按区间尾从小到大，区间头从小到大排序然后贪心就好

AC代码

#include 
using namespace std;
 
typedef pair <int,int> P;
 
int main()
{
    int n,ans = 0;
    P a[10005];
    cin >> n;
    for(int i = 0;i < n;i++) cin >> a[i].second >> a[i].first;
    sort(a,a + n,less<P>());  ##  利用pair自带的cmp函数
     
    int x = -1;
    for(int i = 0;i < n;i++){
        if(x < a[i].second){  ##  相等能钉在一起，因为这是区间
            ans++;
            x = a[i].first;
        }
    }
    cout << ans << endl;
    return 0;
}

F-标准部件 （贪心）

某公司生产了一些标准部件，这些部件有固定的尺寸（xi）和重量（yi）。为了更好地加工它们，需要分组，使每一组的部件都能排成一个尺寸和重量都不下降（若i

Input

第一行为一个整数N（N<=1000），表示部件的个数。第二行有N对正整数，每对正整数表示这些部件的尺寸和重量，均不超过10000。

Output

    Output will consist of a series of lines. Each line will consist of a single word that is a relative ananagram in the input dictionary. Words must be output in lexicographic (case-sensitive) order. There will always be at least one relative ananagram.

Sample Input

5
8 4 3 8 2 3 9 7 3 5

Sample Output

2

理解

	其实和导弹拦截差不多的贪心方式
	先保证其中一行是非降序，在看另外一行来确认分几个组，因为循环循序是一定的，必然先开出来的组的最大值，会比后开出来的组的最大值大

AC代码

#include 
using namespace std;
 
typedef pair<int,int> P;
 
int main()
{
    int n;
    P bj[1010];
    cin >> n;
    for(int i = 0;i < n;i++) cin >> bj[i].first >> bj[i].second;
    sort(bj,bj + n,less<P>() );
     
    int as[1010] = {0};
    as[0] = bj[0].second;
    int ans = 1,k = 1;
    for(int i = 1; i < n;i++){
        bool f = 0;
        for(int j = 0; j < k;j++){
            if(bj[i].second < as[j]) f = 1;  ##  假设会开新的组
            else{
                f = 0;
                as[j]=bj[i].second;  ##  更新最高高度
                break;
            }
        }
        if(f){
            as[k] = bj[i].second;
            k++;
            ans++;
        }
    }
    cout << ans << endl;
    return 0;
}

G-便利店 （贪心）

天宝来到便利店想买些饮料。便利店有各种型号的瓶装饮料售卖，不同型号的饮料卖不同的价格。1瓶0.25升的卖A元，1瓶0.5升的饮料卖B元，1瓶1升的卖C元，1瓶2升的卖D元。便利店里每种饮料都是无限供应。

天宝要买N升的饮料，最少需要花多少钱呢？聪明的你写个程序帮她算算吧。

已知

1） 1≤A,B,C,D≤108 ，1≤N≤109

2） 输入的数据都是整数

Input

输入数据按照下面格式

A B C D

N

Output

输出天宝要买N升的饮料所需要花的钱最小值。

Sample Input

20 30 70 90
3

Sample Output

150

理解

	简单的贪心，被long long卡了一下
	大概就是算单位价格，然后整取就好了

AC代码

#include 
using namespace std;
 
struct node{
    long long val,tj,dval;
};
 
bool comp(node a,node b){
    return a.dval < b.dval;
}
 
int main()
{
    node a[4];
    long long n;
    a[0].tj = 25;a[1].tj = 50;a[2].tj = 100;a[3].tj = 200;
    for(int i = 0;i < 4;i++){cin >> a[i].val;}
    a[0].dval = a[0].val * 8;  ##  防止整除丢失精度
    a[1].dval = a[1].val * 4;
    a[2].dval = a[2].val * 2;
    a[3].dval = a[3].val;
    cin >> n;
    n *= 100;
    sort(a,a+4,comp);
     
    long long sum = 0;
    for(int i = 0;i < 4;i++){
        sum += n/a[i].tj*a[i].val;
        n %= a[i].tj;
    }
    cout << sum << endl;
    return 0;
}

因为输入的是整数，其实可以除了2升之外的都做 归一处理（老师的方法），比这么写优秀很多，代码也好些，这里就不写一遍了

H-循环比赛日程表 （分治）

设有N个选手进行循环比赛，其中N=2M，要求每名选手要与其他N-1名选手都赛一次，每名选手每天比赛一次，循环赛共进行N-1天，要求每天没有选手轮空。

Input

M（1<=M<=6）

Output

表格形式的比赛安排表，每个数占3列。

Sample Input

3

Sample Output

1 2 3 4 5 6 7 8
2 1 4 3 6 5 8 7
3 4 1 2 7 8 5 6
4 3 2 1 8 7 6 5
5 6 7 8 1 2 3 4
6 5 8 7 2 1 4 3
7 8 5 6 3 4 1 2
8 7 6 5 4 3 2 1

理解

	这题规律也不难找，将其分成四块，你会发现左上右下，右上左下是完全相同的，所以，考虑缩小规模写这一题，写着一个递归即可
	刚开始想岔了，想成了2*2 4*4 8*8等比方法，只对小规模进行处理，发现怎么写都写不出来
	后来换了个dfs思路发现就能过了，分治的方法很重要，注意选用合适的方法进行操作

AC代码

#include 
using namespace std;
const double eps = 1e-6;
 
int maps[70][70],n;
 
void dfs(int x,int y,int m){
    if(m == 1) return;
    dfs(x,y,m/2);  ##  等比缩小规模，处理刚开始1 2那一块
    dfs(x + m/2,y,m/2);  ##  要处理4*4时左下角那一块，不然填不出来
     
    for(int i = 0;i < m/2;i++){
        for(int j = 0;j < m/2;j++){
            maps[x + m/2 + i][y + m/2 + j] = maps[x + i][y + j];  ##  右下填涂
            maps[x + i][y + m/2 + j] = maps[x + m/2 + i][y + j];  ##  右上填涂
        }
    }
}
 
int main(){
    cin >> n;
    n = 1 << n;
    for(int i = 0;i < n;i++) maps[i][0] = i + 1;  ##  对第一列进行处理，使后面能进行复制
    dfs(0,0,n);
    for(int i = 0;i < n;i++){
        for(int j = 0;j < n;j++){
            printf("%3d",maps[i][j]);
        }
        printf("\n");
    }
    return 0;
}

I-麦森数 （高精度，压位）

形如2P-1的素数称为麦森数，这时P一定也是个素数。但反过来不一定，即如果P是个素数，2P-1不一定也是素数。到2016年底，人们已找到了49个麦森数。

美国中央密苏里大学数学家库珀领导的研究小组通过参加一个名为“互联网梅森素数大搜索”(GIMPS)项目，于2016年1月7日发现了第49个梅森素数——274207281-1。该素数也是目前已知的最大素数，有22338618位。这是库珀教授第四次通过GIMPS项目发现新的梅森素数，刷新了他的记录。他上次发现第48个梅森素数257,885,161-1是在2013年1月，有17425170位。

梅森素数在当代具有重大意义和实用价值。它是发现已知最大素数的最有效途径，其探究推动了“数学皇后”——数论的研究，促进了计算技术、密码技术、程序设计技术和计算机检测技术的发展。难怪许多科学家认为，梅森素数的研究成果，在一定程度上反映了一个国家的科技水平。英国数学协会主席马科斯 索托伊甚至认为它的研究进展不但是人类智力发展在数学上的一种标志，也是整个科技发展的里程碑之一。

Input

输入P（1000

Output

输出共11行。

第1行：十进制高精度数2P-1的位数；

第2-11行：十进制高精度数2P-1的最后500位数字（每行输出50位，共输出10行，不足500位时高位补0）；

不必验证2P-1与P是否为素数。

Sample Input

1279

Sample Output

386
00000000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000
00000000000000104079321946643990819252403273640855
38615262247266704805319112350403608059673360298012
23944173232418484242161395428100779138356624832346
49081399066056773207629241295093892203457731833496
61583550472959420547689811211693677147548478866962
50138443826029173234888531116082853841658502825560
46662248318909188018470682222031405210266984354887
32958028878050869736186900714720710555703168729087

理解

	这是一道刚开始让人摸不着头脑的题目，看完直接自闭
	后来和大佬一顿分析，得出一些结论
	（1）位数可以用log10(2^p-1)+1来求，又问题二的倍数末尾都是2,4,6,8，所以显而易见，减一不会出现10的倍数，等同于log10(2^p)+1 = p*log10(2)+1
	（2）第二点大佬是用了递归快速幂的方法求的高精度，刚开始不懂，不过看高精度的时候看到一个叫做压位的东西，可以用来减少循环次数，果断用之，
	成功ac

AC代码

#include 
using namespace std;
const long long val = 10000000000;
  
long long p,k;
long long a[60];
void cal(){
    a[1] = 1;
    while(p >= 25){  ##  按2^25做乘法，减少循环次数，不能开太大，会溢出，2^30次溢出
        k = 0;
        for(int i = 1;i <= 50;i++){
            a[i] = (a[i] << 25) + k;
            k = a[i]/val;  ##  10000000000进制中间的过程要自己写进位
            a[i] %= val;
        }
        p -= 25;
    }
    k = 0;
    for(int i = 1;i <= 50;i++){  ##  把最后小于25次的处理掉
        a[i] = (a[i] << p) + k;
        k = a[i]/val;
        a[i] %= val;
    }
    return;
} 
  
int main()
{
    cin >> p;
    cout << (int)(p*log10(2) + 1) << endl;  ##  输出位数
    cal();
    a[1]--;
    int f = 0;
    for(int i = 50;i >= 1;i--){  ##  输出500位
        printf("%010lld",a[i]);  ##  空位补0，控制格式
        f++;
        if(f == 5){
            f = 0;
            printf("\n");
        }
    }
    return 0;
}

J-向右看齐 （贪心，中位数）

新学年开始了。有一批新生要军训了。休息时间到了，同学们站在自己喜欢的位置。每个位置由整数坐标(x,y)表示。同学们可以向前、向后、向左、向右移动一步，但在同一时刻任一位置点上只能有一名同学。按照教官的指令“向右看齐”，同学们要整齐地列成一个水平队列，即排列成(x,y),(x+1,y),…,(x+n-1,y)。如何选择x 和y的值才能使同学们用最少的总移动步数排成一列呢？ 有请作为编程高手的你，计算一下同学们排成一行所需要移动的最少步数。

Input

输入数据有多行。第1 行是学生人数n，1≤n≤10000。接下来n 行是同学们的初始位置，每行2个整数x 和y，-10000≤x，y≤10000。

Output

输出同学们排成一行所需要移动的最少步数。

Sample Input

5
1 2
2 2
1 3
3 -2
3 3

Sample Output

8

理解

	看上去很复杂的题目，要求你找到第一个人的坐标(x,y)，然后以他开始排成一列，叫你计算所有同学走到相应队列所花的时间（走的时候不能两个人
	同时站在一个坐标点上）。
	这种问题我们很容易可以想到，把人分为从两边都早上y轴上，再在y轴上调整位置
	从两边到y轴我们可以看做是找中位线
	而在y轴上的调整，可以看做每个人到固定位置的距离总和最小，也能看做找一个中位线
	所以这道题可以看做找两个中位线即可

AC代码

#include 
using namespace std;
  
int main(){
    int n;
    cin >> n;
    int x[10005],y[10005];
    for(int i = 0;i < n;i++){
        cin >> x[i] >> y[i];
    }
    sort(x,x+n);
    for(int i = 0;i < n;i++) x[i] = x[i] - i;  ##  第i个人到i位置的距离
     
    sort(x,x+n);
    sort(y,y+n);
     
    int k1 = x[(n - 1)/2],k2 = y[(n - 1)/2];  ##  找出两条中位线
    int sum = 0;
    for(int i = 0;i < n;i++){
        sum += abs(k1 - x[i]);  ##  计算累加和
        sum += abs(k2 - y[i]);
    }
    cout << sum << endl;
    return 0;
}

（二）vj例题记录

A-Dropping Balls （思维题） UVA - 679

    A number of K balls are dropped one by one from the root of a fully binary tree structure FBT. Each time the ball being dropped first visits a non-terminal node. It then keeps moving down, either follows the path of the left subtree, or follows the path of the right subtree, until it stops at one of the leaf nodes of FBT. To determine a ball’s moving direction a flag is set up in every non-terminal node with two values, either false or true. Initially, all of the flags are false. When visiting a non-terminal node if the flag’s current value at this node is false, then the ball will first switch this flag’s value, i.e., from the false to the true, and then follow the left subtree of this node to keep moving down. Otherwise, it will also switch this flag’s value, i.e., from the true to the false, but will follow the right subtree of this node to keep moving down. Furthermore, all nodes of FBT are sequentially numbered, starting at 1 with nodes on depth 1, and then those on depth 2, and so on. Nodes on any depth are numbered from left to right.
    For example, Fig. 1 represents a fully binary tree of maximum depth 4 with the node numbers 1,2, 3, …, 15. Since all of the flags are initially set to be false, the first ball being dropped will switch flag’s values at node 1, node 2, and node 4 before it finally stops at position 8. The second ball being dropped will switch flag’s values at node 1, node 3, and node 6, and stop at position 12. Obviously, the third ball being dropped will switch flag’s values at node 1, node 2, and node 5 before it stops at position 10.
    Fig. 1: An example of FBT with the maximum depth 4 and sequential node numbers.
    Now consider a number of test cases where two values will be given for each test. The first value is D, the maximum depth of FBT, and the second one is I, the I-th ball being dropped. You may assume the value of I will not exceed the total number of leaf nodes for the given FBT.
    Please write a program to determine the stop position P for each test case.
    For each test cases the range of two parameters D and I is as below:
    2 ≤ D ≤ 20, and 1 ≤ I ≤ 524288.

Input

Contains l + 2 lines.
Line 1 l the number of test cases
Line 2 D1 I1 test case #1, two decimal numbers that are separated by one blank
…
Line k + 1 Dk Ik test case #k
Line l + 1 Dl Il test case #l
Line l + 2 -1 a constant ‘-1’ representing the end of the input file

Output

Contains l lines.
Line 1 the stop position P for the test case #1
…
Line k the stop position P for the test case #k
…
Line l the stop position P for the test case #l

Sample Input

5
4 2
3 4
10 1
2 2
8 128
-1

Sample Output

12
7
512
3
255

理解

	题目大意就是一颗满二叉树的结点上有一个键值（true或flase），flase往右，true往左，问第x个球最终的位置在哪
	刚开始直接无脑复制acm的模拟代码提交，发现tle了，异常自闭
	后面找了一下规律，发现每个节点往左往右只要看上一个节点的次数/2做一个判断即可
	用这种方式直接找第x个球的移动轨迹，得到下标，成功ac

AC代码

#include 
using namespace std;
 
int main()
{
    int t;
    cin >> t;
    t++;
    while(t--){
    	int d,x,k;
    	cin >> d;
    	if(d == -1) break;
    	cin >> x;
        k = 1;
        
       	for(int j = 1;j < d;j++){
            if(x % 2){
                x = (x + 1)/2;
                k = k*2;
            }
            else{
                x /= 2;
                k = k*2 + 1;
            }
        }
        
    	cout << k << endl;
    }
    return 0;
}

B-Trees on the level（模拟建树） UVA - 122

    Trees are fundamental in many branches of computer science (Pun definitely intended). Current stateof-the art parallel computers such as Thinking Machines’ CM-5 are based on fat trees. Quad- and octal-trees are fundamental to many algorithms in computer graphics.
    This problem involves building and traversing binary trees.
    Given a sequence of binary trees, you are to write a program that prints a level-order traversal of each tree. In this problem each node of a binary tree contains a positive integer and all binary trees have have fewer than 256 nodes.
    In a level-order traversal of a tree, the data in all nodes at a given level are printed in left-to-right order and all nodes at level k are printed before all nodes at level k + 1.
    For example, a level order traversal of the tree on the right is: 5, 4, 8, 11, 13, 4, 7, 2, 1.
    In this problem a binary tree is specified by a sequence of pairs ‘(n,s)’ where n is the value at the node whose path from the root is given by the string s. A path is given be a sequence of ‘L’s and ‘R’s where ‘L’ indicates a left branch and ‘R’ indicates a right branch. In the tree diagrammed above, the node containing 13 is specified by (13,RL), and the node containing 2 is specified by (2,LLR). The root node is specified by (5,) where the empty string indicates the path from the root to itself. A binary tree is considered to be completely specified if every node on all root-to-node paths in the tree is given a value exactly once.

Input

The input is a sequence of binary trees specified as described above. Each tree in a sequence consists of several pairs ‘(n,s)’ as described above separated by whitespace. The last entry in each tree is ‘()’.
No whitespace appears between left and right parentheses.
    All nodes contain a positive integer. Every tree in the input will consist of at least one node and
no more than 256 nodes. Input is terminated by end-of-file.

Output

For each completely specified binary tree in the input file, the level order traversal of that tree should
be printed. If a tree is not completely specified, i.e., some node in the tree is NOT given a value or a
node is given a value more than once, then the string ‘not complete’ should be printed.

Sample Input

(11,LL) (7,LLL) (8,R)
(5,) (4,L) (13,RL) (2,LLR) (1,RRR) (4,RR) ()
(3,L) (4,R) ()

Sample Output

5 4 8 11 13 4 7 2 1
not complete

理解

	这题写起来还蛮有难度的，刚开始想用数组建树，看一下256个节点，自动放弃该想法（2^256 - 1）内存装不下，后面使用链表模拟建树，成功ac
	要注意一下几点
	（1）当建树过程中发现同一位置重复赋值，说明非法，输出错误
	（2）树的连接上有连不上的部分，说明非法，输出错误

AC代码

#include 
using namespace std;

vector <int> ans;
bool f = 0;
struct node{
	bool fz;
    int val;
    node *left,*right;
    node(int val = 0,bool fz = 0,node *left = NULL,node *right = NULL):val(val),fz(fz),left(left),right(right){}
} *root;

void build(int v,string s,node* x){  ##  建树过程，没去过的地方就分配新的内存，但表示没被赋值过
	for(int i = 0;i < s.size();i++){
		if(s[i] == 'L'){
			if(x -> left == NULL) x -> left = new node();
			x = x -> left;
		}
		else if(s[i] == 'R'){
			if(x -> right == NULL) x -> right = new node();
			x = x -> right;
		}
	}
	if(x -> fz) f = 1;  ##  如果重复赋值，标记非法
	x -> fz = 1;
	x -> val = v;
	
	return;
}

bool read(){  ##  读取输入，他的输入很难处理，学大佬写一个read才处理掉
	string s;
	root = new node();  ##  创造树根
	ans.clear();
	f = 0;
	while(cin >> s){
		if(s == "()") break;
		
		int v,k = s.find(',');
		string p;
		v = atoi(s.substr(1,k - 1).c_str());
		p = s.substr(k + 1,s.size() - k - 2);
		build(v,p,root);  ##  根据得到的字符串和值建立链表树
	}
	return !cin.eof();
}

bool bfs(node *root){
	queue <node*> q;
	q.push(root);
	
	while(!q.empty()){  ##  层遍历链表数得到答案准备输出
		node* temp = q.front();q.pop();
		
		if(!(temp -> fz)) return 0;  ##  如果这个地方没赋值过，说明树断了，非法，直接退出
		ans.push_back(temp -> val);
		if(temp -> left != NULL) q.push(temp -> left);
		if(temp -> right != NULL) q.push(temp -> right);
	}
	
	return 1;
}

int main()
{	
	while(read()){
		if(f) cout << "not complete" << endl;
		else if(!bfs(root)) cout << "not complete" << endl;
		else{
			cout << ans[0];
			for(int i = 1;i < ans.size();i++) cout << ' ' << ans[i];
			cout << endl;
		}
	}
	return 0;
}

C-Not so Mobile （栈的运用） UVA - 839

    Before being an ubiquous communications gadget, a mobile was just a structure made of strings and wires suspending colourfull things. This kind of mobile is usually found hanging over cradles of small babies.
    The figure illustrates a simple mobile. It is just a wire,suspended by a string, with an object on each side. It can also be seen as a kind of lever with the fulcrum on the point where the string ties the wire. From the lever principle we know that to balance a simple mobile the product of the weight of the objects by their distance to the fulcrum must be equal. That is Wl × Dl = Wr × Dr where Dl is the left distance,
Dr is the right distance, Wl is the left weight and Wr is the right weight.

    In a more complex mobile the object may be replaced by a sub-mobile, as shown in the next figure.In this case it is not so straightforward to check if the mobile is balanced so we need you to write a program that, given a description of a mobile as input, checks whether the mobile is in equilibrium or not.

Input

    The input begins with a single positive integer on a line by itself indicating the number of the cases following, each of them as described below. This line is followed by a blank line, and there is also a blank line between two consecutive inputs.
    The input is composed of several lines, each containing 4 integers separated by a single space.
    The 4 integers represent the distances of each object to the fulcrum and their weights, in the format:
    Wl Dl Wr Dr
    If Wl or Wr is zero then there is a sub-mobile hanging from that end and the following lines define the the sub-mobile. In this case we compute the weight of the sub-mobile as the sum of weights of all its objects, disregarding the weight of the wires and strings. If both Wl and Wr are zero then the following lines define two sub-mobiles: first the left then the right one.

Output

For each test case, the output must follow the description below. The outputs of two consecutive cases will be separated by a blank line.
Write ‘YES’ if the mobile is in equilibrium, write ‘NO’ otherwise.

Sample Input

1
0 2 0 4
0 3 0 1
1 1 1 1
2 4 4 2
1 6 3 2

Sample Output

YES

理解

	这题刚开始相差了，以为只要每对子节点权重一样即可，后来发现还要考虑树的平衡
	可以参考UVA - 1596 找Bug 中递归解决[]的方式，用递归解决这题，返回子树累加的重量即可

AC代码

#include 
using namespace std;
 
bool f = 1;
int dfs(){
	int w1,d1,w2,d2;
	cin >> w1 >> d1 >> w2 >> d2;
	
	if(!w1) w1 = dfs();  ##  如果左边重量为空，要得到其子树的质量
	if(!w2) w2 = dfs();  ##  同理，得到右边子树的质量
	
	if(w1*d1 != w2*d2) f = 0;  ##  如果不能平衡，标记为f = 0；
	
	return w1 + w2;  ##  返回质量和
}
 
int main()
{	
	int t;
	cin >> t;
	while(t--){
		f = 1;
		dfs();
		if(f) cout << "YES" << endl;
		else cout << "NO" << endl;
		if(t) cout << endl;
	}
    return 0;
}

D-Strange fuction （玄学退火） HDU - 2899

Now, here is a fuction:
        F(x) = 6 * x^7+8*x6+7x^3+5*x2-yx (0 <= x <=100)
Can you find the minimum value when x is between 0 and 100.

Input

The first line of the input contains an integer T(1<=T<=100) which means the number of test cases. Then T lines follow, each line has only one real numbers Y.(0 < Y <1e10)

Output

Just the minimum value (accurate up to 4 decimal places),when x is between 0 and 100.

Sample Input

2
100
200

Sample Output

-74.4291
-178.8534

理解

	第一道写的退火题，第一次接触退火感觉这算法是真的玄学，然而深入了解之后，又对这种神奇的模拟方法感到惊叹
	后面会详细讲讲我对退火的理解

AC代码

#include 
using namespace std;
const double eps = 1e-8;

double y;
double func(double x) {return 6*pow(x,7.0) + 8*pow(x,6.0) + 7*pow(x,3.0) + 5*pow(x,2.0) - y*x;}  ##  能量函数

double th(){
	double T = 100;
	double delta = 0.98;
	double x = 50.0;
	double now = func(x);
	double ans = now;
	while(T > eps){
		int f[2] = {1,-1};
		double newx = x + f[rand() % 2] * T;  ##  随机产生新的位置（x）
		if(newx >= 0 && newx <= 100){  ##  控制范围（这题可以这么控制）
			double next = func(newx);
			ans = min(ans,next);
			if(now - next > eps) {x = newx;now = next;}  ##  误差移动
		}
		T *= delta;
	}
	return ans;
}

int main()
{
	int t;
	cin >> t;
	while(t--){
		cin >> y;
		printf("%.4f\n",th());
	}
	return 0;
}

E-coins （贪心） HDU - 3348

“Yakexi, this is the best age!” Dong MW works hard and get high pay, he has many 1 Jiao and 5 Jiao banknotes(纸币), some day he went to a bank and changes part of his money into 1 Yuan, 5 Yuan, 10 Yuan.(1 Yuan = 10 Jiao)
“Thanks to the best age, I can buy many things!” Now Dong MW has a book to buy, it costs P Jiao. He wonders how many banknotes at least,and how many banknotes at most he can use to buy this nice book. Dong MW is a bit strange, he doesn’t like to get the change, that is, he will give the bookseller exactly P Jiao.

Input

T(T<=100) in the first line, indicating the case number.
T lines with 6 integers each:
P a1 a5 a10 a50 a100
ai means number of i-Jiao banknotes.
All integers are smaller than 1000000.

Output

Two integers A,B for each case, A is the fewest number of banknotes to buy the book exactly, and B is the largest number to buy exactly.If Dong MW can’t buy the book with no change, output “-1 -1”.

Sample Input

3
33 6 6 6 6 6
10 10 10 10 10 10
11 0 1 20 20 20

Sample Output

6 9
1 10
-1 -1

理解

	题目大意就是找出能组成P的最少纸币数和最多纸币数量
	最少纸币数量非常好求，因为纸币的面额被设置为两倍及以上，所以简单的贪心就能算出来
	最多纸币数量刚开始有两个想法，就是大额换小额，但感觉写起来太麻烦了，就进行了另一个方法的尝试
	设所有纸币的面值总和为sum ， 纸币总数量为 k
	当我们对P取最小纸币数量m时，我们能得到（sum-P）的最多纸币数量为k - m
	如果理解不了多想想就好
	所以，我们反向求（sum-P）的最小纸币数量，做差，即可得到P的最多纸币数量

AC代码

#include 
using namespace std;

int coins[] = {1,5,10,50,100};

int minh(int p,int a[]){  ##  求最小纸币数量
	int sum = 0;
	for(int i = 4;i >= 0;i--){
		int k = p/coins[i] > a[i] ?a[i] :p/coins[i];
		sum += k;
		p -= k*coins[i];
		if(!p) break;
	}
	return !p ?sum :-1;  ##  要考虑能否取到P这个总和的纸币
}

int main()
{
	int t;
	cin >> t;
	while(t--){
		int p,a[5] = {0},sum = 0,cnt = 0;
		cin >> p;
		for(int i = 0;i < 5;i++){
			cin >> a[i];
			sum += a[i]*coins[i];
			cnt += a[i];
		}
		int mins = 0,maxs = 0;
		
		mins = minh(p,a);  ##  最少纸币数量
		maxs = cnt - minh(sum - p,a);  ##  最多纸币数量
		
		if(mins != -1 && maxs != -1) cout << mins << ' ' << maxs << endl;
		else cout << "-1 -1" << endl;
	}
	return 0;
}

F-Task （贪心） HDU - 4864

Today the company has m tasks to complete. The ith task need xi minutes to complete. Meanwhile, this task has a difficulty level yi. The machine whose level below this task’s level yi cannot complete this task. If the company completes this task, they will get (500xi+2yi) dollars.
The company has n machines. Each machine has a maximum working time and a level. If the time for the task is more than the maximum working time of the machine, the machine can not complete this task. Each machine can only complete a task one day. Each task can only be completed by one machine.
The company hopes to maximize the number of the tasks which they can complete today. If there are multiple solutions, they hopes to make the money maximum.

Input

The input contains several test cases.
The first line contains two integers N and M. N is the number of the machines.M is the number of tasks(1 < =N <=100000,1<=M<=100000).
The following N lines each contains two integers xi(0 The following M lines each contains two integers xi(0

Output

For each test case, output two integers, the maximum number of the tasks which the company can complete today and the money they will get.

Sample Input

1 2
100 3
100 2
100 1

Sample Output

1 50004

理解

	题目大意就是给出你有机器数量，以及他能处理的任务的时间上限和级别上限，并且给出所有任务的时间和级别，要你求出最多能得到多大的收益
	500*xi+2*yi 求收益的公式
	因为x和y至少为1，所以我们可以发现在求收益方面x的权重远大于y的权重，所以我们按x从小到大再y从小到大的方式排个序
	之后的想法刚开始是趋向于上周atcoder的第四题，因为两者的贪心思路高度类似，但难点是这里没有给出级别上限，所以我们写法就不同了
	优先处理时间长度在范围内，且优先级最低的任务（因为高级别的任务只有高级别的机器能处理，而低级别则不是，简单的贪心思路）

AC代码

#include 
using namespace std;

typedef pair <int,int> P;

int main()
{
	int n,m;
	while(cin >> n >> m){
		P mac[100010],task[100010];
		for(int i = 0;i < n;i++) cin >> mac[i].first >> mac[i].second;
		for(int i = 0;i < m;i++) cin >> task[i].first >> task[i].second;
		
		sort(mac,mac+n,greater<P>());
		sort(task,task+m,greater<P>());
		
		int cnt = 0,k = 0,a[110] = {0};
		long long sum = 0;
		for(int i = 0;i < m;i++){
			while(mac[k].first >= task[i].first){  ##  把时间上能处理这个任务的机器找出来，先存起来
				a[mac[k].second]++;
				k++;
			}
			
			for(int j = task[i].second;j <= 100;j++){  ##  优先给级别低的机器
				if(a[j]){
					a[j]--;
					sum += task[i].first*500 + task[i].second*2;  ##  累计收益
					cnt++;
					break;
				}
			}
		}
		cout << cnt << ' ' << sum << endl;
	}
	return 0;
}

G-Radar Installation （贪心） POJ - 1328

Assume the coasting is an infinite straight line. Land is in one side of coasting, sea in the other. Each small island is a point locating in the sea side. And any radar installation, locating on the coasting, can only cover d distance, so an island in the sea can be covered by a radius installation, if the distance between them is at most d.

We use Cartesian coordinate system, defining the coasting is the x-axis. The sea side is above x-axis, and the land side below. Given the position of each island in the sea, and given the distance of the coverage of the radar installation, your task is to write a program to find the minimal number of radar installations to cover all the islands. Note that the position of an island is represented by its x-y coordinates.

Figure A Sample Input of Radar Installations

Input

The input consists of several test cases. The first line of each case contains two integers n (1<=n<=1000) and d, where n is the number of islands in the sea and d is the distance of coverage of the radar installation. This is followed by n lines each containing two integers representing the coordinate of the position of each island. Then a blank line follows to separate the cases.

The input is terminated by a line containing pair of zeros

Output

For each test case output one line consisting of the test case number followed by the minimal number of radar installations needed. “-1” installation means no solution for that case.

Sample Input

3 2
1 2
-3 1
2 1

1 2
0 2

0 0

Sample Output

Case 1: 2
Case 2: 1

理解

	题目大意，找到能覆盖所有海岛的雷达的最小值（雷达一定在x轴上），如果有覆盖不了的，输出-1
	刚开始写这题的思路就是单纯的往右拉圆圈，每次都要计算理圆心的距离，写起来贼麻烦
	后来换了个角度，从雷达考虑，得出每个可以被雷达覆盖到的区间，题目就成了找反应所有区间的点的最小集合
	和acm上写过的题目不谋而合，简单ac

AC代码

#include 
#include 
#include 
#include 
#include 
using namespace std;

typedef pair <double,double> P;

int main()
{
	P a[1010];
	int n,cnt = 0;
	double r;
	while(~scanf("%d%lf",&n,&r) && n && r){
		for(int i = 0;i < n;i++) scanf("%lf%lf",&a[i].first,&a[i].second);
		
		int f = 0;
		for(int i = 0;i < n;i++){
			if(a[i].second > r){
				f = -1;
				break;
			}
			else{
				double d = sqrt(r*r - a[i].second*a[i].second);
				a[i].second = a[i].first - d;  ##  转换为海岛能被雷达覆盖到的区间
				a[i].first = a[i].first + d;
			}
		}
		
		if(f) printf("Case %d: %d\n",++cnt,f);
		else{
			sort(a,a+n,less<P>());
			double x = a[0].first;
			int sum = 1;
			for(int i = 1;i < n;i++){  ##  求最小集合
				if(a[i].second > x){
					x = a[i].first;
					sum++;
				}
			}
			printf("Case %d: %d\n",++cnt,sum);
		}
	}
	return 0;
}

H-Buried memory （最小覆盖圆） HDU - 3007

Each person had do something foolish along with his or her growth.But,when he or she did this that time,they could not predict that this thing is a mistake and they will want this thing would rather not happened.
The world king Sconbin is not the exception.One day,Sconbin was sleeping,then swakened by one nightmare.It turned out that his love letters to Dufein were made public in his dream.These foolish letters might ruin his throne.Sconbin decided to destroy the letters by the military exercises’s opportunity.The missile is the best weapon.Considered the execution of the missile,Sconbin chose to use one missile with the minimum destruction.
Sconbin had writen N letters to Dufein, she buried these letters on different places.Sconbin got the places by difficult,he wants to know where is the best place launch the missile,and the smallest radius of the burst area. Let’s help Sconbin to get the award.

Input

There are many test cases.Each case consists of a positive integer N(N<500,^V,our great king might be a considerate lover) on a line followed by N lines giving the coordinates of N letters.Each coordinates have two numbers,x coordinate and y coordinate.N=0 is the end of the input file.

Output

For each case,there should be a single line in the output,containing three numbers,the first and second are x and y coordinates of the missile to launch,the third is the smallest radius the missile need to destroy all N letters.All output numbers are rounded to the second digit after the decimal point.

Sample Input

3
1.00 1.00
2.00 2.00
3.00 3.00
0

Sample Output

2.00 2.00 1.41

理解

	又是神奇的退火算法，此处也是仅给代码，套模板即可，后面会详细写自己的理解

AC代码

#include 
using namespace std;
const double eps = 1e-8;

struct node{
	double x,y;
} p[510];

int n;
double ansx,ansy,r;
double getr(double x,double y){  ##  能力函数，算目前这个点的最大半径
	double dx,dy,tr = 0;
	for(int i = 0;i < n;i++){
		dx = x - p[i].x;
		dy = y - p[i].y;
		tr = max(sqrt(pow(x - p[i].x,2) + pow(y - p[i].y,2)),tr);
	}
	return tr;
}

void th(){
	double T = 10;
	double delta = 0.95;
	r = getr(ansx,ansy);
	while(T > eps){
		double x = ansx + (rand()*2-RAND_MAX)*T;
		double y = ansy + (rand()*2-RAND_MAX)*T;
		double d = getr(x,y);
		double k = d - r;
		if(k < eps){
			ansx = x;
			ansy = y;
			r = d;
		}
		else if(exp(-k/T) > rand()){  ##  选择接受
			ansx = x;
			ansy = y;
		}
		T *= delta;
	}
	return;
}

int main()
{
	while(cin >> n && n){
		ansx = 0,ansy = 0;
		for(int i = 0;i < n;i++){
			cin >> p[i].x >> p[i].y;
			ansx += p[i].x;
			ansy += p[i].y;
		}
		ansx /= n;  ##  假定他们和做除法为中心点
		ansy /= n;
		
		th();
		printf("%.2lf %.2lf %.2lf\n",ansx,ansy,r);
	}
	return 0;
}

（三）其他地方的例题记录

A-Polynomial （签到题） 百度之星2019初赛一

度度熊最近学习了多项式和极限的概念。
现在他有两个多项式 f(x) 和 g(x)，他想知道当 x 趋近无限大的时候，f(x)/g(x) 收敛于多少。

Input

第一行一个整数 T (1≤T≤100) 表示数据组数。
对于每组数据，第一行一个整数 n (1≤n≤1,000)，n−1 表示多项式 f 和 g 可能的最高项的次数（最高项系数不一定非0）。
接下来一行 n 个数表示多项式 f，第 i 个整数 fi (0≤fi≤1,000,000) 表示次数为 i−1 次的项的系数。
接下来一行 n 个数表示多项式 g，第 i 个整数 gi (0≤gi≤1,000,000) 表示次数为 i−1 次的项的系数。
数据保证多项式 f 和 g 的系数中至少有一项非0。

Output

对于每组数据，输出一个最简分数 a/b（a 和 b 的最大公约数为1）表示答案。
如果不收敛，输出 1/0。

Sample Input

3
2
0 2
1 0
2
1 0
0 2
3
2 4 0
1 2 0

Sample Output

1/0
0/1
2/1

样例描述
这些多项式分别为
$f(x)=2x$
$g(x)=1$
$f(x)=1$
$g(x)=2x$
$f(x)=4x+2$
$g(x)=2x+1$

理解

	高数学的不好，刚开始一眼看过去直接懵逼，后来和大佬手动算了算可能性，发现题目就是从最高次项开始
	找起，找到其中一项不为0的位置，做一个比较即可
	假设分子系数为x，分母系数为y
	如果x = 0，y != 0 易得极限收敛于0
	如果x != 0，y = 0 易得极限发散
	如果x != 0，y != 0 易得极限收敛于(x/gcd(x,y))/(y/gcd(x,y))

AC代码

签到题，代码简单，不做注释
#include 
using namespace std;

int gcd(int a,int b){
    return b == 0 ?a :gcd(b,a%b);
}

int main()
{    
    int t;
    cin >> t;
    while(t--){
        int n;
        int f[1005],g[1005];
        cin >> n;
        for(int i = 0;i < n;i++) cin >> f[i];
        for(int i = 0;i < n;i++) cin >> g[i];
        
        int x = -1,y = -1;
        for(int i = n - 1;i >= 0;i--){
            if(f[i] == 0 && g[i] == 0) continue;
            x = f[i];
            y = g[i];
            break;
        }
        
        if(y == 0) printf("1/0\n");
        else if(x == 0) printf("0/1\n");
        else{
            int k = gcd(x,y);
            printf("%d/%d\n",x/k,y/k);
        }
    }
    return 0;
}

B-Seq（签到题） 百度之星2019初赛一

度度熊有一个递推式 an=(∑n−1i=1ai∗i)%n
其中 a1=1。现给出 n，需要求 an。

Input

第一行输入一个整数 T，代表 T (1≤T≤100000) 组数据。
接下 T 行，每行一个数字 n (1≤n≤1012)。

Output

输出 T 行，每行一个整数表示答案。

Sample Input

5
1
2
3
4
5

Sample Output

1
1
0
3
0

理解

	第一眼看完数据，发现太大了，暴力求解完全不可能
	自动打表找规律，经过几次修改后，可得规律以6做循环，就简单a掉了
	（不知道正解是啥，蒟蒻只能找找规律这种，也算对于这种找规律的题型练了练手）

AC代码

签到题，代码简单，不做注释
#include 
using namespace std;

int main()
{    
    int t;
    cin >> t;
    while(t--){
        long long n,ans;
        cin >> n;
        if(n % 6 == 1) ans = 1 + n/6*4;
        if(n % 6 == 2) ans = 1 + n/6*3;
        if(n % 6 == 3) ans = n/6;
        if(n % 6 == 4) ans = 3 + n/6*6;
        if(n % 6 == 5) ans = n/6;
        if(n % 6 == 0) ans = n/2;
        printf("%lld\n",ans);
    }
    return 0;
}

C-度度熊与排列 （伪签到题） 百度之星2019初赛二

度熊有一个机器，这个机器有一个 1∼M 的排列 p[1…M] 当作参数，若丢进一个长度为 M 的字符串，此机器会将此字符串重新排列后再输出，重新排列的方式为：原本第 i 个位置的字符会变到第 p[i] 个位置。

举例来说，当 M=3，p[1]=3,p[2]=1,p[3]=2，那么丢 “abc” 进入这个机器后，机器会输出"bca";若丢进的是 “ded”，那么机器会输出 “edd”。

某天，度熊不小心忘记这个机器的参数了，只记得参数的长度是 M，于是他丢了 N 长度为 M 的字符串进去，并记录下对于每个字符串机器的输出结果，请你根据这些结果，帮度熊找回这个机器的参数。若有多组参数都满足度熊的记录，请输出字典序最小的排列作为参数。若并不存在任何参数满足度熊的记录，请输出 −1。

注：对于两个相异的排列a: a[1…M] 和 b[1…M]，我们称 a 比 b 小当且仅当 存在一个 i，满足对于所有小于 i 的 j 都有 aj=bj 且 ai

Input

有多组询问，第一行包含一个正整数 T 代表有几组询问。

每组询问的第一行包含两个正整数 N,M，分别代表度熊丢进机器的字符串数目以及参数的长度。接下来还有 2×N 行，每行有一个长度为 M 的字符串，当中的第 2×i−1 行的字符串代表度熊丢进去机器的第 i 个字符串，而第 2×i 行的字符串代表机器对于第 i 个字符串的输出结果。

• 1≤T≤100

• 1≤N≤20

• 1≤M≤50

• 字符串由英文小写字母(‘a’ 至 ‘z’) 组成

Output

对于每一个询问，输出一行，若不存在任何参数满足度熊的记录，这行只包含一个整数 −1。否则这行包含一个排列，代表此机器所有可能的参数中字典序最小的那个。

Sample Input

4
1 3
abc
bca
2 4
aaab
baaa
cdcc
cccd
3 3
aaa
aaa
bbb
bbb
ccc
ccc
1 1
a
z

Sample Output

3 1 2
2 4 3 1
1 2 3
-1

Note
第一组询问中， $p[1]=3,p[2]=1,p[3]=2$ 是唯一的机器可能的参数。

第二组询问中， $p=[2,4,3,1]$ 和 $p=[3,4,2,1]$ 都是机器可能的参数，不过 $[2,4,3,1]$ 的字典序比 $[3,4,2,1]$ 还小，故必须输出 2,4,3,1。

理解

	刚开始尝试写了一个dfs，毫无意外直接超时
	后面开始思考题意，发现本质上就是对i位置可以移动的方向做一个记录，找到所有组都能使用的数字即可
	因为找的方式是从小到大，自动完成了找最小字典序的任务

AC代码

#include 
using namespace std;

map <int,int> p[55];
bool vis[55];

int main()
{
    int t;
    cin >> t;
    while(t--){
        memset(vis,0,sizeof(vis));
        for(int i = 0;i < 52;i++) p[i].clear();
        
        string a,b;
        int n,l;
        cin >> n >> l;
        for(int i = 0;i < n;i++){
            cin >> a >> b;
            for(int j = 0;j < l;j++){
                for(int k = 0;k < l;k++){
                    if(a[j] == b[k]) p[j][k]++;  ##  记录该位置能去的位置
                }
            }
        }
        
        vector <int> ss;
        map <int,int> :: iterator it;
        for(int i = 0;i < l;i++){
            for(it = p[i].begin();it != p[i].end();it++){
                if(it -> second == n && !vis[it -> first]){  ##  已经被使用过的数字无法被使用，且该数字的出现次数达到组数才能被采用
                    vis[it -> first] = 1;
                    ss.push_back(it -> first + 1);
                    break;
                }
            }
        }
        
        if(ss.size() != l) cout << -1 << endl;  ##  如果找出来的数字数量和长度不符，说明无解
        else{
            cout << ss[0];
            for(int i = 1;i < ss.size();i++) cout << ' ' << ss[i];
            cout << endl;
        }
    }
    return 0;
}

D-RGB Balls （贪心） Atcoder Grand 037

Time Limit: 2 sec / Memory Limit: 1024 MB

Score :
800
points

Problem Statement
We have 3N colored balls with IDs from 1 to 3N. A string S of length 3N represents the colors of the balls. The color of Ball i is red if Si is R, green if Si is G, and blue if Si is B. There are N red balls, N green balls, and N blue balls.

Takahashi will distribute these 3N balls to N people so that each person gets one red ball, one blue ball, and one green ball. The people want balls with IDs close to each other, so he will additionally satisfy the following condition:

Let aj Then, ∑j(cj−aj) should be as small as possible.

Find the number of ways in which Takahashi can distribute the balls. Since the answer can be enormous, compute it modulo 998244353. We consider two ways to distribute the balls different if and only if there is a person who receives different sets of balls.

Constraints
1≤N≤105
|S| = 3N
S consists of R, G, and B, and each of these characters occurs N times in S.

理解

	题目大意，把3*n个球分给n个人，每个人必须得到R,B,G三种球，且得到的球的序号必须是从小到大的，问
	在最后一个球的序号减去第一个球的序号的累加和最小的情况下，有多少种分配方式
	
	这题主要还是死在了题意上，题意刚开始没看懂，以为必须要按R,G,B的方式得到球，导致样例都弄不出来
	，后来看完题解才理解题意（蒟蒻的常态），贪心思路并不难想，对于已有的组合，优先完成肯定是距离最
	小的，对于同时有两者满足组合条件，先后对距离总和并无影响，可以自己想几个样例试试，思路会更清晰
	点，因此，开6个槽位储存已有的不同组合即可，因为未完成的组合只有R,G,B,RG,RB,GB

AC代码

#include 
#define MOD 998244353
using namespace std;
typedef long long ll;
// 1 = R 2 = B 3 = G 4 = RG 5 = RB 6 = GB

int main()
{
	ll n,ans = 1;
	ll a[7] = {0};
	string s;
	cin >> n >> s;
	a[0] = n;  ##  0下标的位置存人数，1~6存未完成组的状态和数量
	
	for(int i = 0;i < s.size();i++){
		if(s[i] == 'R'){  ##  三者类似，就讲一个
			if(a[6]) {ans = ans*a[6]%MOD;a[6]--;}  ##  先看GB有没有
			else if(a[2]) {ans = ans*a[2]%MOD;a[2]--;a[5]++;}  ##  再看B有没有
			else if(a[3]) {ans = ans*a[3]%MOD;a[3]--;a[4]++;}  ##  再看G有没有，这两种上下变化无区别
			else {ans = ans*a[0]%MOD;a[0]--;a[1]++;}  ##  如果都没有，拿一个人，新开一个组
		}
		else if(s[i] == 'B'){
			if(a[4]) {ans = ans*a[4]%MOD;a[4]--;}
			else if(a[1]) {ans = ans*a[1]%MOD;a[1]--;a[5]++;}
			else if(a[3]) {ans = ans*a[3]%MOD;a[3]--;a[6]++;}
			else {ans = ans*a[0]%MOD;a[0]--;a[2]++;}
		}
		else{
			if(a[5]) {ans = ans*a[5]%MOD;a[5]--;}
			else if(a[2]) {ans = ans*a[2]%MOD;a[2]--;a[6]++;}
			else if(a[1]) {ans = ans*a[1]%MOD;a[1]--;a[4]++;}
			else {ans = ans*a[0]%MOD;a[0]--;a[3]++;}
		}
	}
	
	cout << ans << endl;
	return 0;
}

E-Numbers on a Circle （贪心，迭代） Atcoder Grand 037

Time Limit: 2 sec / Memory Limit: 1024 MB
Score : 800 points

Problem Statement
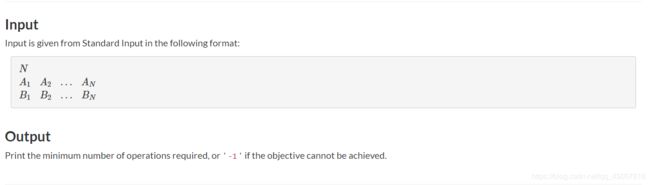
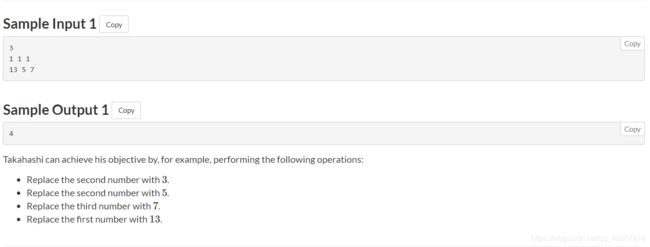
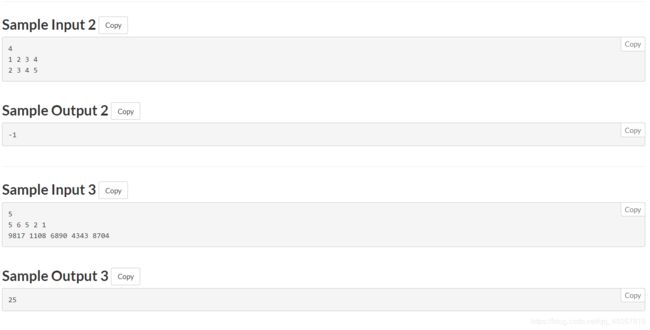
There are N positive integers arranged in a circle.

Now, the i-th number is Ai. Takahashi wants the i-th number to be Bi. For this objective, he will repeatedly perform the following operation:

Choose an integer i such that 1≤i≤N.Let a,b,c be the (i−1)-th, i-th, and (i+1)-th numbers, respectively. Replace the i-th number with a+b+c.
Here the 0-th number is the N-th number, and the (N+1)-th number is the 1-st number.

Determine if Takahashi can achieve his objective. If the answer is yes, find the minimum number of operations required.

Constraints
3≤N≤2×1051≤Ai,Bi≤109
All values in input are integers.

理解

	题目大意，要求把环状数组a变成环状数组b，求所用的最小次数
	变化方式：i - 1，i，i + 1，位置i的值加上i - 1和i + 1上的值
	第一反应bfs，看完数据大小果断放弃，果真写不出来
	后来看完题解，他提到把b变成a，且从b最大值用迭代的方式直接无限接近或直接等于a位置上的值
	刚开始真的没想通为啥能用这种方式得到结果，但后来想了想，给了自己一个可能还算合理的解释？

	要在某个位置上以最少的次数达到要求的值，最简单的做法，把相邻位置的值提到最大后，进行数次迭代
	即可，那么反向从大往小的变化正好反推了这个过程，实现了最小步数（贪心的思维）

AC代码

#include 
using namespace std;
 
struct node{  ##  定义结构体，记录当前位置的下标和值
	int val,idx;
	node(int val,int idx):val(val),idx(idx){}
	friend bool operator < (node a,node b){
		return a.val < b.val;
	}
};
 
int n;
int a[200010],b[200010];
 
int pre(const int i) {return (i+n-1)%n;}  ##  找它前一个位置的值
int pot(const int i) {return (i+n+1)%n;}  ##  同理，后一个位置
bool check(const int i){return (b[i] > a[i] && b[i] - a[i] >= b[pre(i)] + b[pot(i)]);}  ##  检查是否可以放入优先队列中bfs
priority_queue <node> q;  ##  用来实现每次找最大的值优先迭代
 
int main()
{
	long long ans = 0;
	cin >> n;
	for(int i = 0;i < n;i++) cin >> a[i];
	for(int i = 0;i < n;i++){
		cin >> b[i];
		if(a[i] > b[i]){
			cout << -1 << endl;
			return 0;
		}
	}
	
	for(int i = 0;i < n;i++) {if(check(i)) q.push(node(b[i],i));}  ##  判断能否迭代，要求b[i] - b[i-1] + b[i+1] >= a[i],才可以进行迭代
	
	while(!q.empty()){
		node temp = q.top();q.pop();
		int dis = temp.val - a[temp.idx];
		int dis2 = b[pre(temp.idx)] + b[pot(temp.idx)];
		ans += dis/dis2;
		b[temp.idx] = a[temp.idx] + dis%dis2;
		if(check(pre(temp.idx))) q.push(node(b[pre(temp.idx)],pre(temp.idx)));  ##  简单i-1是否再该操作后满足迭代的调节
		if(check(pot(temp.idx))) q.push(node(b[pot(temp.idx)],pot(temp.idx)));  ##  同上
	}
	
	for(int i = 0;i < n;i++){
		if(a[i] != b[i]){  ##  如果无法完场，必然有值不相等，输出-1
			cout << -1 << endl;
			return 0;
		}
	}
	cout << ans << endl;  ##  否则输出答案即可
	return 0;
}

F-[JSOI2004]平衡点 / 吊打XXX （退火） 洛谷P1337

如图：有n个重物，每个重物系在一条足够长的绳子上。每条绳子自上而下穿过桌面上的洞，然后系在一起。图中X处就是公共的绳结。假设绳子是完全弹性的（不会造成能量损失），桌子足够高（因而重物不会垂到地上），且忽略所有的摩擦。

问绳结X最终平衡于何处。

注意：桌面上的洞都比绳结X小得多，所以即使某个重物特别重，绳结X也不可能穿过桌面上的洞掉下来，最多是卡在某个洞口处。

Input

文件的第一行为一个正整数n（1≤n≤1000），表示重物和洞的数目。接下来的n行，每行是3个整数：Xi.Yi.Wi，分别表示第i个洞的坐标以及第 i个重物的重量。(-10000≤x,y≤10000, 0

Output

你的程序必须输出两个浮点数（保留小数点后三位），分别表示处于最终平衡状态时绳结X的横坐标和纵坐标。两个数以一个空格隔开。

Sample Input

3
0 0 1
0 2 1
1 1 1

Sample Output

0.577 1.000

理解

	老师找的blog推荐的退火题目，姑且做了尝试，尝试完之后才知道退火调参有多难受
	问最后平衡在何处，根据简单的物理知识，能量越小越稳定，能量最小的点也就是最后的平衡点
	套个退火模板，慢慢调参吧（交了20来次，永远卡一个点，提交到快自闭）

AC代码

#include 
using namespace std;
  
const double eps = 1e-15;
 
struct node{
	int x,y,w;
} p[1005];

int n;
double ansx,ansy,anse;

double gete(double x,double y){  ##  能量函数
	double tx,ty,eng = 0;
	for(int i = 0;i < n;i++){
		tx = x - p[i].x;
		ty = y - p[i].y;
		eng += sqrt(tx*tx + ty*ty)*p[i].w;
	}
	return eng;
}

void sa(){  ##  经典退火模板
	double t = 2500;
	double detla = 0.997;
	anse = gete(ansx,ansy);
	while(t > eps){
		double nowx = ansx + (rand()*2-RAND_MAX)*t;  ##  生成正负-32768~32767
		double nowy = ansy + (rand()*2-RAND_MAX)*t;
		double nowe = gete(nowx,nowy);
		double k = nowe - anse;
		if(k < eps){
			ansx = nowx;
			ansy = nowy;
			anse = nowe;
		}
		else if(exp(-k/t)*RAND_MAX>rand()){  ##  概率接受，后面收获那里有细讲
			ansx = nowx;
			ansy = nowy;
		}
		t *= detla;
	}
}

int main()
{
	cin >> n;
	ansx = 0;ansy = 0;
	for(int i = 0;i < n;i++){
		cin >> p[i].x >> p[i].y >> p[i].w;
		ansx += p[i].x;
		ansy += p[i].y;
	}
	ansx /= n;ansy /= n;
	sa();sa();
	printf("%.3lf %.3lf\n",ansx,ansy);
	return 0;
}

也是第一道感受到退火玄学之处的题目，试了别人的参数都出不来，最后试了两页的题解参数靠运气ac，退火确实要慎用，不过退火还是蛮有趣的，接下来有空打算在洛谷怼一点退火练练

（四）一些收获

关于树（数据结构）

之前是接触过链表的，确实在学树的时候有一定的帮助（链表建树在空间上的优势极大），建树这一块感觉也没啥好谈的，目前学的大概也就四类（学的还比较浅）

	1.根据中序 + 前序/后序/层序 建树，方法也是比较简单，此处不贴代码，只要对建树有理解随便建
	2.根据先序加特殊的方式，如加入. #之类的符号建树，也比较简单
	3.建二分字典树，也挺简单的，每次从树根遍历向下即可
	4.建huffman树（最优编码树[得到最短编码]），个人使用链表加优先队列实现了，不过写了蛮久的，有点难度，这个贴一下代码

huffman树

#include 
using namespace std;
   
struct node{
	int val;
	char x;
	node *left,*right;
	node(int val = 0,char x = 0,node *left = NULL,node *right = NULL):val(val),x(x),left(left),right(right){}
};

map <char,string> p;

struct comp{  ##  定义优先队列的比较方式
	bool operator () (node *x,node *y){
		if(x -> val != y -> val) return x -> val > y -> val;
		else{
		    	if(x -> left != NULL) return x -> val >= y -> val;
		    	if(y -> left != NULL) return y -> val >= x -> val;
		    	return 0;
		}
	}
};

void dfs(node* root,string s){  ##  先序遍历找出编码
	if(root -> left == NULL && root -> right == NULL){
		p[root -> x] = s;
		return;
	}

	if(root -> left != NULL) dfs(root -> left,s + "0");
	if(root -> right != NULL) dfs(root -> right,s + "1");

	return;
}

node* build(node* a,node* b){  ##  造树
	node *temp = new node(a -> val + b -> val);
	temp -> left = a;
	temp -> right = b;

	return temp;
}

void removes(node *root){
	if(root == NULL) return;
	removes(root -> left);
	removes(root -> right);
	delete root;
}

int main()
{
	priority_queue <node*,vector<node*>,comp > q;  ##  优先队列存结点
	string s;
	while(cin >> s){
		int sum[200] = {0};
		vector <char> zm;
		for(int i = 0;i < s.size();i++){
			sum[s[i]]++;
			if(find(zm.begin(),zm.end(),s[i]) == zm.end()) zm.push_back(s[i]);
		}
	
		while(!zm.empty()){
			node *temp = new node(sum[zm[0]],zm[0]);
			zm.erase(zm.begin());
			q.push(temp);
		}
	
		while(q.size() > 1){
			node *a = q.top();q.pop();
			node *b = q.top();q.pop();
			
			node *temp = build(a,b);
			q.push(temp);
		}
	
		node *root = q.top();q.pop();
		dfs(root,"");
	
		for(map<char,string>::iterator it = p.begin();it != p.end();it++){
			cout << it -> first << ' ' << it -> second << endl;
		}
	
		removes(root);
		p.clear();
	}
	return 0;
}

关于贪心

之前也是写过不少贪心算法的题，但趋于简单，而且没有对大概类型做一个系统性的学习，这周练完也是对贪心多了不少理解

	1.贪心策略是很灵活的，没有固定的形式（但有些题型就是我们学过的基础贪心模板做一下装饰），应根据题目进行相应的贪心策略的选择
	2.判断你的贪心思路是否可行，最简单的方法就是自行构思一些特殊样例找漏洞，如果问题不大，不妨一试（在没其他想法的情况下）
	3.贪心策略的确定，必须是对题目中每个元素都有一个确定的贪法再进行尝试，思路要清晰，确认每个元素的优先级

说了一堆，其实总结而言，贪心主要就是靠悟性和刷题，刷提是让你最基础的贪心思路得到开阔，而悟性则决定了你对于藏得极深的贪心能否想到合适的贪心策略

简而言之，对于贪心，多想，多练，总会有一定的提高

关于退火（玄学之下的概率算法）

初次接触退火之后蛮感兴趣的，就对其做了一点学习，发现其玄学外表之下的神奇之处，退火拿代码的模板来讲比较合适空谈有点水，姑且拿洛谷 P1337 [JSOI2004]平衡点 / 吊打XXX 来谈谈目前我对退火的看法

#include 
using namespace std;
  
const double eps = 1e-15;  ##  eps,及终止温度，其的大小一定程度上决定了我们所找到得到值的精度，看情况条件即可
 
struct node{
	int x,y,w;
} p[1005];

int n;
double ansx,ansy,anse;

double gete(double x,double y){  ##  能量函数，这题的能量函数式距离和权重的和，实际上能量函数是用来评估当前状态下的结果是否比之前
	double tx,ty,eng = 0;			 的状态更优，不同题目的能量函数不同，看题目来写（个人认为类似于a*算法里的启发函数）
	for(int i = 0;i < n;i++){
		tx = x - p[i].x;
		ty = y - p[i].y;
		eng += sqrt(tx*tx + ty*ty)*p[i].w;
	}
	return eng;
}

void sa(){
	double t = 2500;  ##  起始温度，他决定了迭代次数和搜索范围，根据题意进行调整
	double detla = 0.997;  ##  降温系数，他一定层度上决定了搜索精度，也决定了迭代次数（不能开太大，容易tle）
	anse = gete(ansx,ansy);
	while(t > eps){
		double nowx = ansx + (rand()*2-RAND_MAX)*t;  ##  随机生成下一个目标点，客服“贪心”缺陷
		double nowy = ansy + (rand()*2-RAND_MAX)*t;
		double nowe = gete(nowx,nowy);
		double k = nowe - anse;
		if(k < eps){  ##  如果状态更优，必然接受
			ansx = nowx;
			ansy = nowy;
			anse = nowe;
		}
		else if(exp(-k/t)*RAND_MAX>rand()){  ##  如果状态更差了，用e为低的指数函数进行计算，然后概率接受
			ansx = nowx;
			ansy = nowy;
		}
		t *= detla;
	}
}

int main()
{
	cin >> n;
	ansx = 0;ansy = 0;
	for(int i = 0;i < n;i++){
		cin >> p[i].x >> p[i].y >> p[i].w;
		ansx += p[i].x;  ##  刚开始设立“中点”有利于更快找到结果
		ansy += p[i].y;
	}
	ansx /= n;ansy /= n;
	sa();sa();  ##　多次退火貌似能提升精度
	printf("%.3lf %.3lf\n",ansx,ansy);
	return 0;
}

退火算法实际上而言，是通过极其多次的迭代，使优先级高的地区以极高的概率进入答案，并且剔除优先级低的区域。

做一个简单的推论
（1）在到达优先级更高的区域的情况下，移动必然发生，其必然趋向优先级高的区域
（2）在到达优先级更低的区域的情况下，他概率接受移动（后面详细说说指数函数的作用），就算他发生了移动，在下一步中，他的一部分区域重新变为高优先级，更容易被概率接受，且一旦他离开低优先级的区域，因为搜索范围的收缩，它必然无法回到之前的低优先级区域，随着迭代次数达到一个极大地值，高优先级区域必然被锁定（换一个理解思路，利用指数函数的运算，优先级低到一定程度的区域，因为太小，概率太低，几乎无法到达，而一些优先级稍微低一点的，咋有稍大的概率到达，这就完成了一个翻山的过程）【如果用图来表示这个过程，把到达次数高的地方涂成深色，低的地方则为浅色，应该理解起来会简单很多，用地形图也行，高峰为高概率区域】

关于exp函数
当到达优先级低的区域时，我们代入的分子是负数，根据指数函数可知
（1）分子越小，值越小，相对来说概率也就越低
（2）分子越大，值越大，想多来说概率也就越大
分母为T
（1）T刚开始很大，起到了范围很大时，限制位置移动的作用
（2）T后面很小，起到了小范围内多次移动，寻找顶峰的作用
实际上exp函数是退火算法的灵魂之一（个人认为，另一个是随机值）

关于退火精度
（1）终点温度肯定是能起到一个提高精度的作用的
（2）降温系数在末尾的时候应该也是能起到一个提高精度的作用

简单总结：
（1）如果发现精度不够高，优先调节降温系数和终点温度
（2）如果发现区域不太对，极可能是迭代次数还不够，可以提高降温系数或者起始温度（多次退火应该也有一点帮助）

退火最大缺点：本质而言，退火客服了贪心可能陷入死局的缺点，但能求出来的值，也成了极度逼近答案的近似值，很多时候可能等于答案，但也有很答案相差极小导致无法ac的情况（这题目我交了近20次不断卡一两个点，调了很多次参数），很多题目上，退火终究不是正解，退火更适用于能分段拿分且自己没有正解思路的情况下

一点点小建议（大雾）：
（1）真的调不出ac参数时，可以试试来自东方的神秘质数作为随机数种子19260817（滑稽）
（2）改不出可行参数的时候，拉欧皇朋友帮你改改然后提交

总结而言：退火是一种很神奇且值得学习的算法，退火要会用，并且要慎用

关于分治

分治思想也就起了一个头吧，而且自己用的也不熟，也还只讲了归并排序，下周学完再做一个总结好了

（五）感想

大概就以下几点
1.贪心思维的养成是一个逐渐思考练习的过程，还需要多练习，而且几个典型的贪心模板必须熟练使用，因为这是敲好的模板，很多时候题型转换一下可能就能套，虽然概率比较小，但确实是有价值的

2.注意对于题目本质的理解，这周做的贪心题目，大多都可以归为思维题，也许有些可以暴力搜索或者硬模拟，但终究tle风险很大。类似雷达那题，注意题目的本质就很容易套用已知的实用模板

3.关于建树，建树的过程可能不是解题过程中必备的，有些模拟一个树的过程即可，要注意思考。另一方面，建树也是必须要会的，一方面能帮助暴力过题，一方面有些题以树为数据结构才能做

4.关于退火，这应该是本周学的最有意思的东西了，也是最难理解的东西了，虽然很多时候不能算一个正解，但它存在的价值还是不低的，之后打算在洛谷试着练练，至少达到基础掌握

5.关于分治，这一块感觉自己掌握比较差，很多题就直接暴力a过去了，貌似分治用不太惯？？？，还得加强这方面的学习。

（革命尚未成功，同志尚需努力[狗头]）