R语言实现随机森林

转自简书
链接：http://www.jianshu.com/p/ca09dedb0541

1、让两个以及两个以上组合树变成一颗树：combine()

combine(...)

…：每个随机森林对象

data(iris)
rf1 <- randomForest(Species ~ ., iris, ntree=50, norm.votes=FALSE)
rf2 <- randomForest(Species ~ ., iris, ntree=50, norm.votes=FALSE)
rf3 <- randomForest(Species ~ ., iris, ntree=50, norm.votes=FALSE)
rf.all <- combine(rf1, rf2, rf3)
print(rf.all)

2、从森林中提取一颗树：getTree()

getTree(rfobj, k=1, labelVar=FALSE)

rfobj：随机森林对象
k：提取树的个数
labelVar：FALSE or TRUE，更好的标签被用于分裂变量和预测的类别
对于数值预测，数据与变量的值小于或等于分裂点去到左子节点。
对于分类的预测，分裂点代表一个整数，依据其二进制扩展可以判断该类别是去左子节点还是去右子节点。
例如，如果一个预测四大类，分裂点为13。13的二进制扩展是（1，0，1，1）（因为
13 = 1(2^0)+0(2^1)+1(2^2)+1(2^3)），所以类别1、3或4被预测到左子节点，其余的到右子节点。
一个矩阵（或数据框，如果labelvar = true）六列六行，总数等于树中的节点数。六列是：

左子女：左子节点所在的行；如果节点为终端的话，则为0
右子女：右子节点所在的行；如果节点为终端的话，则为0
分裂的变量：被用来分割的节点；如果节点是终端，则为0
分裂点：最好的分裂点
状态：节点终端（- 1）或不（1）
预测：节点的预测；如果节点不是终端，则为0

## Look at the third trees in the forest.
getTree(randomForest(iris[,-5], iris[,5], ntree=10), 3, labelVar=TRUE)

3、增加树的数量：grow()

grow(x, how.many, ...)

x：随机森林对象
how.many：增加树的数量

data(iris)
iris.rf <- randomForest(Species ~ ., iris, ntree=50, norm.votes=FALSE)
iris.rf <- grow(iris.rf, 50)
print(iris.rf)

4、提取特征的重要性：importance()

importance(x, type=NULL, class=NULL, scale=TRUE, ...)

x：随机森林对象
type ：1或者2,重要性度量类型，1代表均值降序精度，2代表均值降序节点纯度
class：类别度量

set.seed(4543)
data(mtcars)
mtcars.rf <- randomForest(mpg ~ ., data=mtcars, ntree=1000,
keep.forest=FALSE, importance=TRUE)
importance(mtcars.rf)
importance(mtcars.rf, type=1)

5、画图：plot()

plot(x, sort=TRUE, ...)
set.seed(1)
data(iris)
iris.rf <- randomForest(Species ~ ., iris, keep.forest=FALSE)
plot(margin(iris.rf))

6、分类图：MDSplot()

MDSplot(rf, fac, k=2, palette=NULL, pch=20, ...)

rf：随机森林对象
fac：训练随机森林的因子
k：维度数
palette：颜色

set.seed(1)
data(iris)
iris.rf <- randomForest(Species ~ ., iris, proximity=TRUE,
keep.forest=FALSE)
MDSplot(iris.rf, iris$Species)
## Using different symbols for the classes:
MDSplot(iris.rf, iris$Species, palette=rep(1, 3), pch=as.numeric(iris$Species))

7、填补缺失值的中位数：na.roughfix()

na.roughfix(object, ...)

数值变量：缺失值使用中位数替代
因子自变量：缺失值使用最常出现的替代

data(iris)
iris.na <- iris
set.seed(111)
iris.na
## artificially drop some data values.
for (i in 1:4) iris.na[sample(150, sample(20)), i] <- NA
iris.roughfix <- na.roughfix(iris.na)
iris.narf <- randomForest(Species ~ ., iris.na, na.action=na.roughfix)
print(iris.narf)

8、异常值（离群点）：outlier()

outlier(x, ...)
set.seed(1)
iris.rf <- randomForest(iris[,-5], iris[,5], proximity=TRUE)
plot(outlier(iris.rf), type="h",
col=c("red", "green", "blue")[as.numeric(iris$Species)])

9、用图形化描述变量的边际效应（分类或回归）：partialPlot()

partialPlot(x, pred.data, x.var, which.class,
w, plot = TRUE, add = FALSE,
n.pt = min(length(unique(pred.data[, xname])), 51),
rug = TRUE, xlab=deparse(substitute(x.var)), ylab="",
main=paste("Partial Dependence on", deparse(substitute(x.var))),
...)

x：随机森林对象
pred.data：预测数据
x.var：变量名称
which.class：分类数据
w：权重

data(iris)
set.seed(543)
iris.rf <- randomForest(Species~., iris)
partialPlot(iris.rf, iris, Petal.Width, "versicolor")
## Looping over variables ranked by importance:
data(airquality)
airquality <- na.omit(airquality)
set.seed(131)
ozone.rf <- randomForest(Ozone ~ ., airquality, importance=TRUE)
imp <- importance(ozone.rf)
impvar <- rownames(imp)[order(imp[, 1], decreasing=TRUE)]
op <- par(mfrow=c(2, 3))
for (i in seq_along(impvar)) {
  partialPlot(ozone.rf, airquality, impvar[i], xlab=impvar[i],
              main=paste("Partial Dependence on", impvar[i]),
              ylim=c(30, 70),col='blue')
}
par(op)

10、画均值方差：Plot()

plot(x, type="l", main=deparse(substitute(x)), ...)
data(mtcars)
plot(randomForest(mpg ~ ., mtcars, keep.forest=FALSE, ntree=100), log="y",col='red')

11、预测测试数据：predict()

predict(object, newdata, type="response",
norm.votes=TRUE, predict.all=FALSE, proximity=FALSE, nodes=FALSE,
cutoff, ...)

object：随机森林对象
newdata：预测新的数据
type：使用概率矩阵或者还是使用计数投票矩阵
norm.votes：计数投票矩阵标准化
predict.all：是否使用所有的树进行预测
nodes：最终端的节点
cutoff：

data(iris)
set.seed(111)
ind <- sample(2, nrow(iris), replace = TRUE, prob=c(0.8, 0.2))
iris.rf <- randomForest(Species ~ ., data=iris[ind == 1,])
iris.pred <- predict(iris.rf, iris[ind == 2,])
table(observed = iris[ind==2, "Species"], predicted = iris.pred)
## Get prediction for all trees.
predict(iris.rf, iris[ind == 2,], predict.all=TRUE)
## Proximities.
predict(iris.rf, iris[ind == 2,], proximity=TRUE)
## Nodes matrix.
str(attr(predict(iris.rf, iris[ind == 2,], nodes=TRUE), "nodes"))

12、随机森林模型：randomForest()

## S3 method for class ’formula’
randomForest(formula, data=NULL, ..., subset, na.action=na.fail)
## Default S3 method:
randomForest(x, y=NULL, xtest=NULL, ytest=NULL, ntree=500,
mtry=if (!is.null(y) && !is.factor(y))
max(floor(ncol(x)/3), 1) else floor(sqrt(ncol(x))),
replace=TRUE, classwt=NULL, cutoff, strata,
sampsize = if (replace) nrow(x) else ceiling(.632*nrow(x)),
nodesize = if (!is.null(y) && !is.factor(y)) 5 else 1,
maxnodes = NULL,
importance=FALSE, localImp=FALSE, nPerm=1,
proximity, oob.prox=proximity,
norm.votes=TRUE, do.trace=FALSE,
keep.forest=!is.null(y) && is.null(xtest), corr.bias=FALSE,
keep.inbag=FALSE, ...)

## S3 method for class ’randomForest’
print(x, ...)

分类:

> data(iris)
> set.seed(71)
> iris.rf <- randomForest(Species ~ ., data=iris, importance=TRUE,
+ proximity=TRUE)
> print(iris.rf)
Call:
 randomForest(formula = Species ~ ., data = iris, importance = TRUE,      proximity = TRUE) 
               Type of random forest: classification
                     Number of trees: 500
No. of variables tried at each split: 2

        OOB estimate of  error rate: 5.33%
Confusion matrix:
           setosa versicolor virginica class.error
setosa         50          0         0        0.00
versicolor      0         46         4        0.08
virginica       0          4        46        0.08
> round(importance(iris.rf), 2)
             setosa versicolor virginica MeanDecreaseAccuracy
Sepal.Length   6.04       7.85      7.93                11.51
Sepal.Width    4.40       1.03      5.44                 5.40
Petal.Length  21.76      31.33     29.64                32.94
Petal.Width   22.84      32.67     31.68                34.50
             MeanDecreaseGini
Sepal.Length             8.77
Sepal.Width              2.19
Petal.Length            42.54
Petal.Width             45.77
> iris.mds <- cmdscale(1 - iris.rf$proximity, eig=TRUE)
> op <- par(pty="s")
> pairs(cbind(iris[,1:4], iris.mds$points), cex=0.6, gap=0,
+ col=c("red", "green", "blue")[as.numeric(iris$Species)],
+ main="Iris Data: Predictors and MDS of Proximity Based on RandomForest")
> par(op)

无监督案例:

> set.seed(17)
> iris.urf <- randomForest(iris[, -5])
> MDSplot(iris.urf, iris$Species)
> ## stratified sampling: draw 20, 30, and 20 of the species to grow each tree.
> (iris.rf2 <- randomForest(iris[1:4], iris$Species,
+ sampsize=c(20, 30, 20)))

Call:
 randomForest(x = iris[1:4], y = iris$Species, sampsize = c(20,      30, 20)) 
               Type of random forest: classification
                     Number of trees: 500
No. of variables tried at each split: 2

        OOB estimate of  error rate: 5.33%
Confusion matrix:
           setosa versicolor virginica class.error
setosa         50          0         0        0.00
versicolor      0         47         3        0.06
virginica       0          5        45        0.10

回归:

data(airquality)
set.seed(131)
ozone.rf <- randomForest(Ozone ~ ., data=airquality, mtry=3,
                         importance=TRUE, na.action=na.omit)
print(ozone.rf)
## Show "importance" of variables: higher value mean more important:
round(importance(ozone.rf), 2)
## "x" can be a matrix instead of a data frame:
set.seed(17)
x <- matrix(runif(5e2), 100)
y <- gl(2, 50)
(myrf <- randomForest(x, y))
(predict(myrf, x))
## "complicated" formula:
(swiss.rf <- randomForest(sqrt(Fertility) ~ . - Catholic + I(Catholic < 50),
                          data=swiss))
(predict(swiss.rf, swiss))
## Test use of 32-level factor as a predictor:
set.seed(1)
x <- data.frame(x1=gl(53, 10), x2=runif(530), y=rnorm(530))
(rf1 <- randomForest(x[-3], x[[3]], ntree=10))
## Grow no more than 4 nodes per tree:
(treesize(randomForest(Species ~ ., data=iris, maxnodes=4, ntree=30)))
## test proximity in regression
iris.rrf <- randomForest(iris[-1], iris[[1]], ntree=101, proximity=TRUE, oob.prox=FALSE)
str(iris.rrf$proximity)

13、交叉验证进行特征选择：rfcv()

rfcv(trainx, trainy, cv.fold=5, scale="log", step=0.5,
mtry=function(p) max(1, floor(sqrt(p))), recursive=FALSE, ...)
trainx：自变量
trainy：因变量
cv.fold：几折交叉验证
set.seed(647)
myiris <- cbind(iris[1:4], matrix(runif(96 * nrow(iris)), nrow(iris), 96))
result <- rfcv(myiris, iris$Species, cv.fold=3)
with(result, plot(n.var, error.cv, log="x", type="o", lwd=2))
## The following can take a while to run, so if you really want to try
## it, copy and paste the code into R.
## Not run:
result <- replicate(5, rfcv(myiris, iris$Species), simplify=FALSE)
error.cv <- sapply(result, "[[", "error.cv")
matplot(result[[1]]$n.var, cbind(rowMeans(error.cv), error.cv), type="l",
lwd=c(2, rep(1, ncol(error.cv))), col=1, lty=1, log="x",
xlab="Number of variables", ylab="CV Error")
## End(Not run)

14、随机森林填补缺失值：rfImpute ()

## Default S3 method:
rfImpute(x, y, iter=5, ntree=300, ...)

## S3 method for class ’formula’
rfImpute(x, data, ..., subset)

x：自变量
y：因变量

data：数据框
data(iris)
iris.na <- iris
set.seed(111)
## artificially drop some data values.
for (i in 1:4) iris.na[sample(150, sample(20)), i] <- NA
set.seed(222)
iris.imputed <- rfImpute(Species ~ ., iris.na)
set.seed(333)
iris.rf <- randomForest(Species ~ ., iris.imputed)
print(iris.rf)

15、最优抽样：rfImpute()

tuneRF(x, y, mtryStart, ntreeTry=50, stepFactor=2, improve=0.05,
trace=TRUE, plot=TRUE, doBest=FALSE, ...)
data(fgl, package="MASS")
fgl.res <- tuneRF(fgl[,-10], fgl[,10], stepFactor=1.5)

16、变量的重要性：varImpPlot()

arImpPlot(x, sort=TRUE, n.var=min(30, nrow(x$importance)),
type=NULL, class=NULL, scale=TRUE,
main=deparse(substitute(x)), ...)

set.seed(4543)
data(mtcars)
mtcars.rf <- randomForest(mpg ~ ., data=mtcars, ntree=1000, keep.forest=FALSE,
                          importance=TRUE)
varImpPlot(mtcars.rf)

随机森林中决策树分裂方法

https://www.stat.berkeley.edu/~breiman/RandomForests/cc_home.htm
Gini importance
Every time a split of a node is made on variable m the gini impurity criterion for the two descendent nodes is less than the parent node. Adding up the gini decreases for each individual variable over all trees in the forest gives a fast variable importance that is often very consistent with the permutation importance measure.

变量重要性评价

随机森林变量重要性的计算方法有两种，分别是Gini指数和测试集(OOB)错误率。

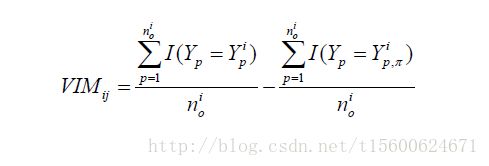
importance(mtcars.rf)
       %IncMSE IncNodePurity
cyl  16.799437     173.03496
disp 18.946107     241.43741
hp   17.282802     186.55081
drat  6.961155      70.14317
wt   19.012343     248.53222
qsec  5.179746      30.64678
vs    5.147341      31.76982
am    5.357654      18.35507
gear  4.324805      16.00897
carb  9.825615      27.77433

其中，%IncMSE和IncNodePurity分别是相对重要性和节点纯度，其中，相对重要性基于OOB错误率，节点纯度基于Gini指数。