武科大许志伟
武科大许志伟

论文研读-多目标优化中的多源选择迁移框架

论文研读-多目标优化中的多源选择迁移框架

Multisource Selective Transfer Framework in Multiobjective Optimization Problems

觉得有用的话,欢迎一起讨论相互学习~

我的微博我的github我的B站

  • 此篇文章为 J. Zhang, W. Zhou, X. Chen, W. Yao and L. Cao, "Multisource Selective Transfer Framework in Multiobjective Optimization Problems," in IEEE Transactions on Evolutionary Computation, vol. 24, no. 3, pp. 424-438, June 2020, doi: 10.1109/TEVC.2019.2926107. 的论文学习笔记，只供学习使用，不作商业用途，侵权删除。并且本人学术功底有限如果有思路不正确的地方欢迎批评指正！

Abstract

  • 在实际复杂系统设计中，当启动具有另一个参数配置的新优化实例时，总是从头开始执行，浪费大量时间重复类似的搜索过程。受可以重用过去经验来解决相关任务的迁移学习的启发，许多研究人员更加注重探索如何从过去的优化实例中学习以加速目标实例。在实际应用中，数据库中已经存储了相似资源实例。 基本问题是如何评价迁移能力以避免负迁移 ， 为了获得源实例与目标实例之间的关联性，我们开发了一种名为质心分布的优化实例表示方法，该方法借助于精英候选解在进化过程中估计分布算法（EDA）中学习的概率模型的帮助。Wasserstein距离用于评估不同优化实例的质心分布之间的相似性，在此基础上，我们提出了一种新颖的框架，称为多源选择性转移优化，其中包括三种合理选择源的策略。为了选择合适的策略，根据源和目标质心分布之间的相似性总结了四个选择建议。该框架有利于选择最合适的资源，从而可以提高解决多目标优化问题的效率。 为了评价提出的框架和选择方法的有效性，我们进行了两个实验：
  1. 复杂多目标优化问题benchmark
  2. 一个实际的卫星布局优化设计问题
    实验结果证明，提出的算法有更好的收敛速度和HV值
  • 摘要：估计分布算法(EDA),多目标优化，多源迁移，迁移优化， Wasserstein distance

Introduction

  • 对于实际工程中的复杂系统设计问题，以卫星系统设计为例，有很多过去的经验，例如在启动新设计之前，已将不同布局的卫星布局解决方案设计存储在数据库中。 利用以往的经验不仅可以提高优化效果，而且可以提高收敛速度。 对于复杂的系统设计而言，这非常重要，因为它通常涉及计算成本高昂的多学科分析[1]。但是，如何利用这些知识来加快新设计的速度，会使卫星设计者感到困惑。 转移学习关注从一个域到另一个域的数据迁移。 各种研究已成功应用于经典机器学习任务，如分类任务[2]-[4]，如情绪分析[5]，数字识别[6]。近年来，进化算法界的研究人员试图将迁移学习应用到优化任务[7]-[10]中。

  • 三个需要关注的问题

  • Q1 (可迁移性) :如何识别相似的问题的可迁移性以降低不合适的负迁移。

  • Q2 (迁移组件) :解决方案，结构，参数等。

  • Q3 (迁移算法) :最后步骤是如何重用从源问题中提取的信息。 大多数研究关注于一对一的域自适应算法，例如MNIST数据集[13]和WIFI数据集[14]等基准测试中的传输成分分析（TCA）[11]，TrAdaBoost [12]。 但是，很少有研究集中在多源迁移学习问题上。

  • 在迁移学习研究领域，大部分工作集中在Q2和Q3，尤其是Q3。 但是，Q1也非常重要，因为从不适当的来源迁移会导致负迁移。 在本文中，我们特别关注多源问题的可迁移性，并研究如何衡量不同优化问题的相似性

  • [15]证明任务间的相关程度对于多任务学习的有效性十分重要,[16]发展了一个基于自编码器的多任务优化算法，其任务选择主要取决于 1)帕累托前沿解的交叉程度2)任务适应度景观的相似性 ，这些因素保证了相关性。 但是，在实际场景中，我们一开始无法获得目标问题的上述信息。

  • 为了评估不同优化问题的相关性，应首先确定不同优化实例的表示形式。Santana et al. [17] 通过一种估计分布算法-估计贝叶斯网络算法（EBNA）将优化问题视为一个图形。 在他的工作中，任务用图形表示。 可以通过网络分析方法获得任务的相关性，但是表示方法在很大程度上取决于人为的图形特征，可能会丢失任务的相关信息。Yu et al. [18] 发明了一种新的表示强化学习任务的表示方法，该学习方法具有通过均匀分布采样的不同参数。他使用原型策略通过几次迭代获得的奖励向量（称为浅试验）来表示任务，从而使过去的强化学习任务得以重用。 但是，演化过程中的浅层试验会产生太多噪声，无法准确表示优化实例。

  • 在每一个世代，利用估计分布算法(EDA)表示种群分布，我们可以利用综合分布来表示实例，在这里称为质心分布。质心表示种群在一个世代中的中心。通过计算实例(任务)分布之间的Wasserstein distance(WD)可以获得任务之间的相似性。有了相似性，可以使用三种不同的基于遗传算法的资源选择策略来获得迁移的知识以加速进化过程中的搜索过程，为了高效使用这种策略，采用四种选择机制

  • 以下是本文的贡献：

  1. 提出一种新的表示方式叫做 质心分布 来度量不同优化实例的相似性
  2. 提出一种新的基于EDA，NSGA-II三种策略的多源选择迁移优化框架来优化多目标优化问题
  3. 总结了迁移资源选择策略的四点建议，在此基础上，提出了应对负迁移问题的混合策略。
  • 以下为本文内容概述：
  1. 第二节总结了迁移学习，EDA(估计分布算法)，进化动态优化算法(EDO)
  2. 第三节总结了基于EDA和NSGA-II的多源选择迁移优化算法的基本框架和流程图
  3. 第四节在多目标烟花算法benchmark上做了实验，并总结了四种资源选择策略并在一个实际问题上验证了算法
  4. 第五节总结了本文算法

Related work

Transfer optimization

  • 最近，开发了许多致力于通过机器学习技术提高现有进化算法效率的工作，尤其是重用了过去从相关问题中获得的搜索经验。Feng [7] 为了解决多目标优化问题，提出了一种基于自动编码器模型的新传输方法，加快了进化算法的搜索过程。
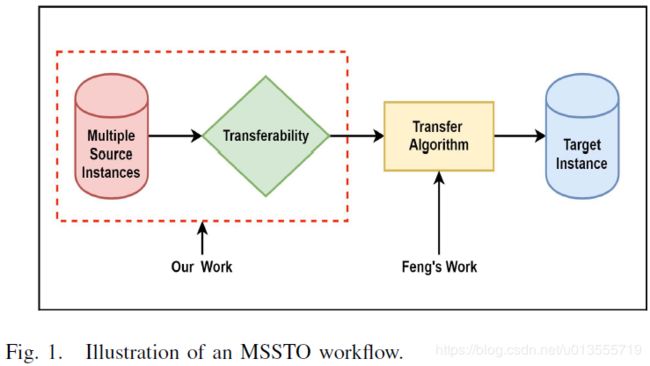
  • 迁移优化可以两类： 单源和多源 ，目前研究大多数是单源迁移算法， 多源优化算法不仅注重迁移方式还注重实例表示和源选择
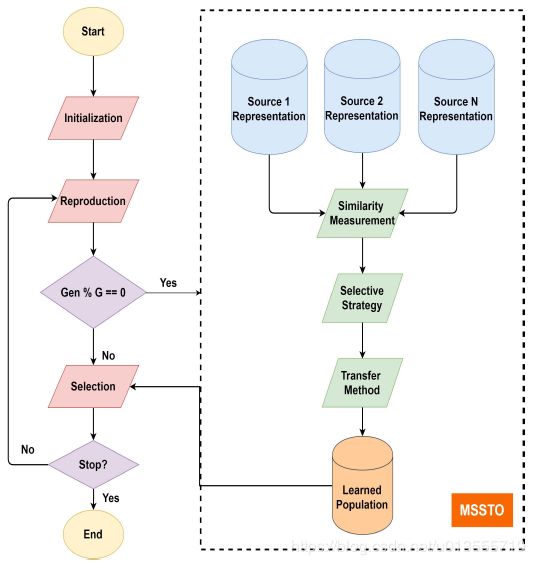
  • 具体算法流程和示意如图1所示：
    论文研读-多目标优化中的多源选择迁移框架_第1张图片

Estimation of Distribution Algorithms 估计分布算法 EDA

  • EDA是随机优化方法，可通过学习和抽样精英候选解决方案的显式概率模型来指导寻找最佳点。 EDA与常规进化算法（遗传算法算法）之间的主要区别在于，后者通过变异和交叉操作生成新的候选解，可以将其视为隐式分布。 但是，EDA使用由概率模型表示的显式分布，例如多元正态分布，贝叶斯网络等。
  • EDA常见算法结构如下图所示：
    论文研读-多目标优化中的多源选择迁移框架_第2张图片

根据决策变量的相互依赖，EDA可以被分为三类：

  1. 单变量分解算法：其中每个变量都是相互独立的。代表算法有： 基于种群的 population-based incremental learning (PBIL) 基于种群的增量学习 [22], univariate marginal distribution algorithm (UMDA) 单变量边际分布算法 [23], compact genetic algorithm (cGA) 紧凑遗传算法 [24], etc.
  2. 二元分解： 在此类模型中， 变量之间的关系形成树或者森林图。双变量分解使变量之间的依赖关系形成树或森林图。 代表性算法包含互 mutual information maximizing input clustering 信息最大化输入聚类（MIMIC）[25]，基于依赖关系树和二元边际分布的估计分布算法[26]等。
  3. 多元分解，使用有向无环图或无向图表示依赖关系 。 贝叶斯网络[27]和马尔可夫网络[28]是两个代表性的模型。
  • 近年来，EDA已用于众多具有挑战性的优化问题，尤其是在多目标优化问题[29]-[33]和多峰优化问题[34]，[35]中。 借助从精英解中学到的概率模型，许多类型的研究[36]都集中于如何重用过去经验中的模型以加速目标实例搜索。 受EDA迁移学习研究的启发，我们提出了一种表示实例的新方法，称为质心分布。 基于表示形式，我们提出了三种资源选择策略来产生合适的知识以进行迁移。

Evolutionary Dynamic Optimization 进化动态优化 EDO

  • EDO是进化计算领域中最活跃的研究领域之一。 在某些EDO情况下，随着环境的变化，问题具有一些常见的模式。 受此启发，许多研究集中在重用类似环境中的过去搜索经验来加速进化过程[37]，[38]。
  1. 一种常见的方法是通过一些特殊的点来学习并预测最优点的移动，Li [39]提出了基于特殊点的预测策略(SPPS):例如feed-forward center point,前馈中心点, boundary point边界点, and knee point拐点。Ruan等人[40]提出了一种基于中心点的混合多样性维护方法，以提高预测精度。 Zou等[41]提出了一种基于拐点来预测非支配集合的方法，以使种群迅速收敛到PF。
  2. 另一种方法是预测发生更改时应重新初始化个体或种群的位置。 Zhou的工作[42]利用历史搜索经验来指导类似的目标搜索，以有效解决动态优化问题。 提出了两种重新初始化策略，一种是根据历史预测个体的新位置。 另一个则是通过某种噪声来扰动 perturb 当前种群，这些噪声的方差由先前的变化估计。
  3. 当环境周期性变化时，第三种方法称为基于memory的方法通常用于通过重用存储在内存中的相关帕累托最优集（POS）信息来解决EDO问题[43]-[46]。 Jiang和Yang[37]提出了一种新的方法，称为稳态和世代进化算法（SGEA），该方法重用了过去分布良好的解，并且当环境发生改变时，根据先前和当前环境的信息重新定位了与新帕累托前沿有关的解 此外，多种群机制是解决问题的有用方法[47]，[48]。
  4. 最近的一些工作直接将迁移学习算法（例如TCA）与动态优化算法集成在一起。 Jiang以此方式提出了两个算法框架。 一种叫做Tr-DMOEA，它结合了迁移学习和基于种群的进化算法[8]，另一种则是领域自适应和基于非参数估计的EDA的组合，称为DANE-EDA [9]。 与他的工作不同，我们主要侧重于如何从多个源任务中选择合适的源以加速进化过程。
  • 本文认为动态问题利用历史信息，但是问题除了某些参数以外，问题的定义没有发生变化，但是迁移学习不一样，其要通过历史信息优化的完全是不一样的两个问题。因此如何度量两个问题的相似性并且选择合适的迁移源将是本文的重点。

多源选择迁移优化框架

  • 现有大多数研究对一对一传输优化更感兴趣，而忽略了实际场景中的多源属性。在本文中，我们提出了一个多源选择性迁移优化框架来解决多源实例的问题。
  • 图2首先引入了实例表示，然后提出了源-目标相似度度量方法，提出了是那种源实例选择策略。
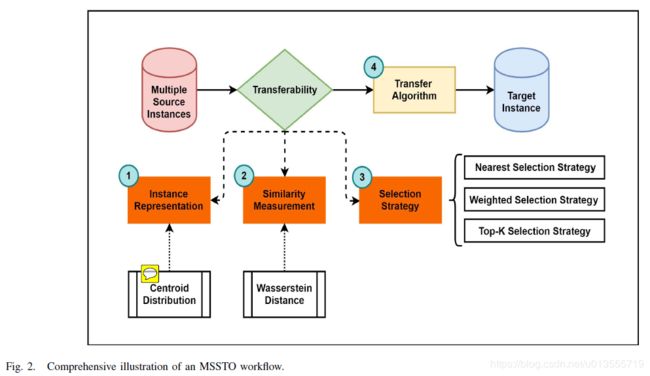
    论文研读-多目标优化中的多源选择迁移框架_第3张图片

优化实例表示

  • 质心表示的源选择策略
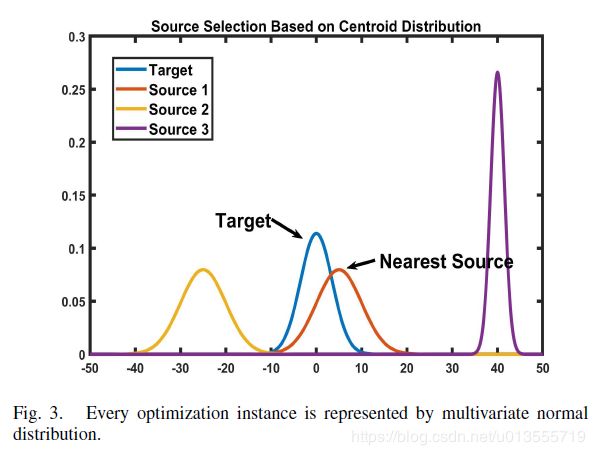
  • 通过运行GA风格的算法，我们可以通过选择操作获得精英群体，可以将选择的解决方案的分布作为EDA的显式概率模型来学习。 我们称其为学习型质心分布，以表示空间中当前的人口扩散趋势。
    论文研读-多目标优化中的多源选择迁移框架_第4张图片
  • 下面的表示很关键，需要注意！
    论文研读-多目标优化中的多源选择迁移框架_第5张图片
  • 为避免负转移，应在迁移算法启动之前确定合适的来源。 我们提出的表示方法可以反映进化过程中源和目标之间的一些相似性信息，可以帮助目标实例选择合适的源进行迁移 。

源和目标相似度度量

  • WD是在给定度量空间[50]上的概率分布之间定义的距离函数。 在本文中，我们使用WD计算源和目标任务质心分布之间的距离。
  • 由于质心分布C满足独立多变量标准分布，WD计算公式如下所示：
    论文研读-多目标优化中的多源选择迁移框架_第6张图片
  • 关于WD和Kullback–Leibler divergence
    可以参考以下博文资料
    多元高斯分布的KL散度
    各维度不相关的多元高斯分布
    多元高斯分布
    两种群决策变量高斯分布的KL散度和WD距离

迁移源选择策略

  • 因为使用不同的优化方法和不同的停止条件，即使是相同的优化任务也会得到不同的优化结果。并且对于高度复杂非线性和具有不同非连接局部最优的多模态优化问题，即使是使用相同的优化算子，每次得到的结果都有可能不一样。因此，即使迁移源看起来很不一样，也许其实是来自相似的任务。 实际上，当给予大量的源数据并且没有优化函数和每个源使用的优化器的先验知识的时候，很难正确判断源与目标之间的差异是否源于任务之间的差异。 因此，在本文中，我们提出了“质心分布的距离越近，实例相关程度越高”的选择策略，这实际上是一个充分但不是必要的条件。 如果距离很近，我们判断实例是相关的并且可以选择。 但是相反，如果实例相关，则我们无法判断分布将是紧密的。
  • 根据以上的分析，根据相似性，提出了三种迁移源选择策略来生成到目标实例的迁移种群，如图4所示。
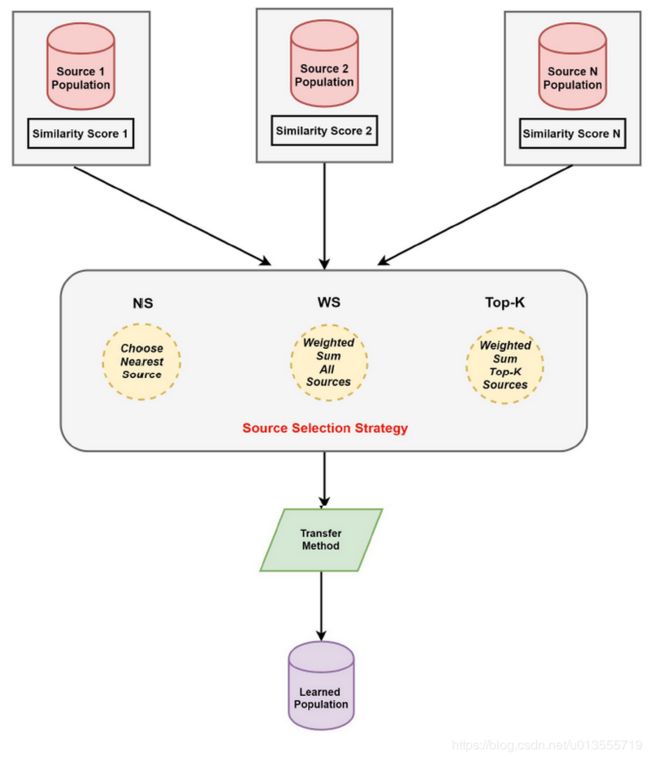
    论文研读-多目标优化中的多源选择迁移框架_第7张图片

最近迁移策略–挑选质心分布最相似的任务进行迁移

论文研读-多目标优化中的多源选择迁移框架_第8张图片
论文研读-多目标优化中的多源选择迁移框架_第9张图片

  • 在NSS中 认为相似程度最高的任务中包含有最有用的迁移知识。

权重选择策略–利用所有资源知识

  • 在某些情况下，某些源可能几乎位于相同的相似度级别（也就是说多个源和目标的相似程度接近，难以挑选）。 如果我们使用一个源进行迁移，则会丢失一些有关其他源的有用信息。 在这种情况下，提出了一种利用所有源知识的新策略。 由于不同源对迁移效率的贡献程度不同，因此最终源是当前这一代所有源的加权总和。 该策略称为加权选择策略（WSS）。
    论文研读-多目标优化中的多源选择迁移框架_第10张图片
  • 这里wi是一个标量，而P是一个矩阵
  • 在WSS中，所有源都是有用的，但是每个源的迁移程度，重要程度不同~

TopK选择策略–按照相似度挑选TopK个源

  • WSS的改进版，按照相似度挑选前K个源
    论文研读-多目标优化中的多源选择迁移框架_第11张图片

策略选择建议

  • 在这一部分中，总结了四个建议，以指导在特定条件下选择合适的选择策略。
  1. 首先，提出最大相似率：
    论文研读-多目标优化中的多源选择迁移框架_第12张图片
  • 这表示相似度最大的源任务能够占所有任务相似度的比。
  1. 相似度的方差引导，决定使用WSS还是TopK
  • 相似度方差小–WSS，相似度方差大–TopK
  • 基于以上分析，选择源选择策略的建议可以总结如下:
  1. 最大相似度msr很大–NSS选择最好的
  2. msr较小，相似度方差小–WSS
  3. msr较小，相似度方差大–TopK
  4. 当msr较低，且方差位于WSS和Top-K策略的临界范围时，不建议调用迁移操作。
    (是否忽视了不依赖相似度从而跳转的可能性？！)
  • 基于以上建议，提出了三种策略的混合版本，称为混合选择策略（MSS）。 为了探索在进化过程中是否在每一代中需要进行转移，将每次触发源选择策略。 根据所有源和目标之间的相似性信息，由以上建议确定是否转移。 更多的相似度计算带来更多的计算成本，但实际上也利用了更多的信息。

Transfer Method 迁移模块

  • 使用[7]中提出的自编码器迁移进化算法进行迁移~
  • 具体而言：
  • 源种群和目标种群可以通过一层具有可靠理论推论的单层去噪自动编码器[7]连接起来。 如图5所示，基于自动编码器的迁移方法的关键是学习从源到目标种群的映射M。
    论文研读-多目标优化中的多源选择迁移框架_第13张图片
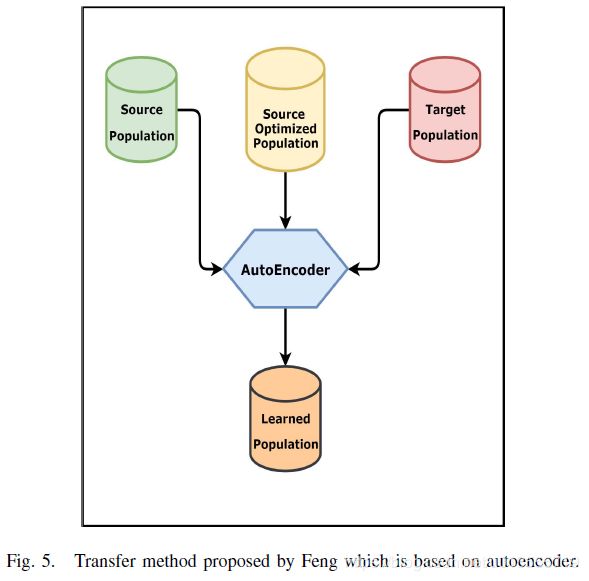
    论文研读-多目标优化中的多源选择迁移框架_第14张图片
  • 需要注意这个映射矩阵是随着迭代不断变化改进的，需要隔一定的世代重新构建一次。以往问题的优化解包含了大量的知识，可以提高目标优化搜索速度，使我们可以通过学习映射将以往经验中的最佳解转移到目标中。
  • 迁移矩阵最终由以下式子进行确定：
    论文研读-多目标优化中的多源选择迁移框架_第15张图片

Proposed Framework 提出的框架

  • 提出的MSSTO的算法框架如图6所示，伪代码如算法2所示，G设置为10：
    论文研读-多目标优化中的多源选择迁移框架_第16张图片
    论文研读-多目标优化中的多源选择迁移框架_第17张图片
  • 其中使用的候选解有
  1. 上一代种群
  2. 经过交叉和变异后的子代种群
  3. 经过迁移算法得到的种群
  • 初始化之后，框架开始执行种群重组，信息迁移和选择操作的循环。为节省计算量，迁移操作只有在世代为G的倍数的时候调用，迁移算子被调用时，源实例和目标实例首先由质心分布表示，质心分布首先由（1）和（2）定义。然后，可以通过（3）和（4）来计算源和目标之间的相似性得分。接下来，将根据（5）–（9）选择合适的迁移源。最后，由（10）和（11）产生要迁移的学习种群。完成最终适应性评估后，循环停止。 （5）-（9）中定义的三种选择策略可以为转移方法的后续过程提供最终的源种群。该策略不仅可以提高优化效果，而且可以提高收敛速度，从而减少适应性评价量。实际应用中较少的评估意味着更少的模拟或实验，从而可以节省大量的计算或实验成本。

参考文献

[1] W. Yao, X. Chen, Q. Ouyang, and M. V. Tooren, “A reliability-based multidisciplinary design optimization procedure based on combined probability and evidence theory,” Struct. Multidiscipl. Optim., vol. 48, no. 2, pp. 339–354, 2013.
[2] C. B. Do and A. Y. Ng, “Transfer learning for text classification,” in Proc. 18th Adv. Neural Inf. Process. Syst., Vancouver, BC, Canada, Dec. 2005, pp. 299–306. [Online]. Available: http://papers.nips.cc/paper/2843-transfer-learning-for-text-classification
[3] A. Quattoni, M. Collins, and T. Darrell, “Transfer learning for image classification with sparse prototype representations,” in Proc. IEEE Comput. Soc. Conf. Comput. Vis. Pattern Recognit. (CVPR), Anchorage, AK, USA, Jun. 2008, pp. 1–8. [Online]. Available: https://doi.org/10.1109/CVPR.2008.4587637
[4] S. J. Pan and Q. Yang, “A survey on transfer learning,” IEEE Trans. Knowl. Data Eng., vol. 22, no. 10, pp. 1345–1359, Oct. 2010. [Online]. Available: https://doi.org/10.1109/TKDE.2009.191
[5] Y. Yoshida, T. Hirao, T. Iwata, M. Nagata, and Y. Matsumoto, “Transfer learning for multiple-domain sentiment analysis— Identifying domain dependent/independent word polarity,” in Proc. 25th AAAI Conf. Artif. Intell., San Francisco, CA, USA, Aug. 2011, pp. 1286–1291. [Online]. Available: http://www.aaai.org/ocs/index.php/AAAI/AAAI11/paper/view/3597
[6] H. Hosseinzadeh and F. Razzazi, “LMDT: A weakly-supervised largemargin- domain-transfer for handwritten digit recognition,” Eng. Appl. Artif. Intell., vol. 52, pp. 119–125, Jun. 2016. [Online]. Available: https://doi.org/10.1016/j.engappai.2016.02.014
[7] L. Feng, Y.-S. Ong, S. Jiang, and A. Gupta, “Autoencoding evolutionary search with learning across heterogeneous problems,” IEEE Trans. Evol. Comput., vol. 21, no. 5, pp. 760–772, Oct. 2017. [Online]. Available: https://doi.org/10.1109/TEVC.2017.2682274
[8] M. Jiang, Z. Huang, L. Qiu, W. Huang, and G. G. Yen, “Transfer learning-based dynamic multiobjective optimization algorithms,” IEEE Trans. Evol. Comput., vol. 22, no. 4, pp. 501–514, Aug. 2018. [Online]. Available: https://doi.org/10.1109/TEVC.2017.2771451
[9] M. Jiang, L. Qiu, Z. Huang, and G. G. Yen, “Dynamic multi-objective estimation of distribution algorithm based on domain adaptation and nonparametric estimation,” Inf. Sci., vol. 435, pp. 203–223, Apr. 2018. [Online]. Available: https://doi.org/10.1016/j.ins.2017.12.058
[10] R. Santana, A. Mendiburu, and J. A. Lozano, “Structural transfer using EDAs: An application to multi-marker tagging SNP selection,” in Proc. IEEE Congr. Evol. Comput. (CEC), Brisbane, QLD, Australia, Jun. 2012, pp. 1–8. [Online]. Available: https://doi.org/10.1109/CEC.2012.6252963
[11] S. J. Pan, I. W. Tsang, J. T. Kwok, and Q. Yang, “Domain adaptation via transfer component analysis,” IEEE Trans. Neural Netw., vol. 22, no. 2, pp. 199–210, Feb. 2011. [Online]. Available: https://doi.org/10.1109/TNN.2010.2091281
[12] W. Dai, Q. Yang, G.-R. Xue, and Y. Yu, “Boosting for transfer learning,” in Proc. 24th Int. Conf. Mach. Learn. (ICML), Corvallis, OR, USA, Jun. 2007, pp. 193–200. [Online]. Available: https://doi.org/10.1145/1273496.1273521
[13] Y. Lecun, L. Bottou, Y. Bengio, and P. Haffner, “Gradient-based learning applied to document recognition,” Proc. IEEE, vol. 86, no. 11, pp. 2278–2324, Nov. 1998.
[14] J. G. Rohra, B. Perumal, S. J. Narayanan, P. Thakur, and R. B. Bhatt, “User localization in an indoor environment using fuzzy hybrid of particle swarm optimization & gravitational search algorithm with neural networks,” in Proc. 6th Int. Conf. Soft Comput. Problem Solving, 2017, pp. 286–295.
[15] T. Liu, Q. Yang, and D. Tao, “Understanding how feature structure transfers in transfer learning,” in Proc. 26th Int. Joint Conf. Artif. Intell. (IJCAI), Melbourne, VIC, Australia, Aug. 2017, pp. 2365–2371. [Online]. Available: https://doi.org/10.24963/ijcai.2017/329
[16] L. Feng et al., “Evolutionary multitasking via explicit autoencoding,” IEEE Trans. Cybern., vol. 49, no. 9, pp. 3457–3470, Sep. 2019.
[17] R. Santana, C. Bielza, and P. Larranaga, “Network measures for re-using problem information in EDAs,” Dept. Artif. Intell., Faculty Informat., Tech. Univ. Madrid, Madrid, Spain, Rep. UPM-FI/DIA/2010–3, 2010.
[18] Y. Yu, S.-Y. Chen, Q. Da, and Z.-H. Zhou, “Reusable reinforcement learning via shallow trails,” IEEE Trans. Neural Netw. Learn. Syst., vol. 29, no. 6, pp. 2204–2215, Jun. 2018. [Online]. Available: https://doi.org/10.1109/TNNLS.2018.2803729
[19] K. Deb, A. Pratap, S. Agarwal, and T. Meyarivan, “A fast and elitist multiobjective genetic algorithm: NSGA-II,” IEEE Trans. Evol. Comput., vol. 6, no. 2, pp. 182–197, Apr. 2002.
[20] A. Gupta, Y.-S. Ong, and L. Feng, “Insights on transfer optimization: Because experience is the best teacher,” IEEE Trans. Emerg. Topics Comput. Intell., vol. 2, no. 1, pp. 51–64, Feb. 2018. [Online]. Available: https://doi.org/10.1109/TETCI.2017.2769104
[21] M. Hauschild and M. Pelikan, “An introduction and survey of estimation of distribution algorithms,” Swarm Evol. Comput., vol. 1, no. 3, pp. 111–128, 2011. [Online]. Available: https://doi.org/10.1016/j.swevo.2011.08.003
[22] S. Baluja, “Population-based incremental learning. A method for integrating genetic search based function optimization and competitive learning,” Tech. Rep., 1994. [Online]. Available: https://dl.acm.org/ citation.cfm?id=865123
[23] H. Mühlenbein, “The equation for response to selection and its use for prediction,” Evol. Comput., vol. 5, no. 3, pp. 303–346, 1997. [Online]. Available: https://doi.org/10.1162/evco.1997.5.3.303
[24] G. R. Harik, F. G. Lobo, and D. E. Goldberg, “The compact genetic algorithm,” IEEE Trans. Evol. Comput., vol. 3, no. 4, pp. 287–297, Nov. 1999.
[25] J. S. D. Bonet, C. L. Isbell, and P. Viola, “MIMIC: Finding optima by estimating probability densities,” in Proc. Int. Conf. Neural Inf. Process. Syst., Denver, CO, USA, 1996, pp. 424–430.
[26] M. Pelikan and H. Muehlenbein, The Bivariate Marginal Distribution Algorithm. London, U.K.: Springer, 1999.
[27] M. Pelikan, D. E. Goldberg, and E. Cantú-Paz, “BOA: The Bayesian optimization algorithm,” in Proc. Conf. Genet. Evol. Comput., Orlando, FL, USA, 1999, pp. 525–532.
[28] S. Shakya, J. Mccall, and D. Brown, “Using a Markov network model in a univariate EDA: An empirical cost-benefit analysis,” in Proc. Genet. Evol. Comput. Conf. (GECCO), Washington, DC, USA, Jun. 2005, pp. 727–734.
[29] Y. Gao, L. Peng, F. Li, M. Liu, and X. Hu, “EDA-based multi-objective optimization using preference order ranking and multivariate Gaussian copula,” in Proc. 10th Int. Symp. Neural Netw. Adv. Neural Netw. II (ISNN), Dalian, China, Jul. 2013, pp. 341–350. [Online]. Available: https://doi.org/10.1007/978-3-642-39068-5_42
[30] H. Karshenas, R. Santana, C. Bielza, and P. Larrañaga, “Multiobjective estimation of distribution algorithm based on joint modeling of objectives and variables,” IEEE Trans. Evol. Comput., vol. 18, no. 4, pp. 519–542, Aug. 2014. [Online]. Available: https://doi.org/10.1109/TEVC.2013.2281524
[31] V. A. Shim, K. C. Tan, and C. Y. Cheong, “A hybrid estimation of distribution algorithm with decomposition for solving the multiobjective multiple traveling salesman problem,” IEEE Trans. Syst., Man, Cybern. C, Appl. Rev., vol. 42, no. 5, pp. 682–691, Sep. 2012. [Online]. Available: https://doi.org/10.1109/TSMCC.2012.2188285
[32] V. A. Shim, K. C. Tan, J. Y. Chia, and A. A. Mamun, “Multi-objective optimization with estimation of distribution algorithm in a noisy environment,” Evol. Comput., vol. 21, no. 1, pp. 149–177, Mar. 2013. [Online]. Available: https://doi.org/10.1162/EVCO_a_00066
[33] J. Luo, Y. Qi, J. Xie, and X. Zhang, “A hybrid multi-objective PSO–EDA algorithm for reservoir flood control operation,” Appl. Soft Comput., vol. 34, pp. 526–538, Sep. 2015. [Online]. Available: https://doi.org/10.1016/j.asoc.2015.05.036
[34] P. Lipinski, “Solving the firefighter problem with two elements using a multi-modal estimation of distribution algorithm,” in Proc. IEEE Congr. Evol. Comput. (CEC), Donostia-San Sebastián, Spain, Jun. 2017, pp. 2161–2168. [Online]. Available: https://doi.org/10.1109/CEC.2017.7969566
[35] Q. Yang, W.-N. Chen, Y. Li, C. L. P. Chen, X.-M. Xu, and J. Zhang, “Multimodal estimation of distribution algorithms,” IEEE Trans. Cybern., vol. 47, no. 3, pp. 636–650, Mar. 2017. [Online]. Available: https://doi.org/10.1109/TCYB.2016.2523000
[36] M. Pelikan, M. W. Hauschild, and P. L. Lanzi, “Transfer learning, soft distance-based bias, and the hierarchical BOA,” in Proc. 12th Int. Conf. Parallel Problem Solving Nat. I (PPSN XII), Taormina, Italy, Sep. 2012, pp. 173–183. [Online]. Available: https://doi.org/10.1007/978-3-642- 32937-1_18
[37] S. Jiang and S. Yang, “A steady-state and generational evolutionary algorithm for dynamic multiobjective optimization,” IEEE Trans. Evol. Comput., vol. 21, no. 1, pp. 65–82, Feb. 2017.
[38] S. Jiang and S. Yang, “Evolutionary dynamic multiobjective optimization: Benchmarks and algorithm comparisons,” IEEE Trans. Cybern., vol. 47, no. 1, pp. 198–211, Jan. 2017.
[39] Q. Li, J. Zou, S. Yang, J. Zheng, and R. Gan, “A predictive strategy based on special points for evolutionary dynamic multi-objective optimization,” Soft Comput., vol. 23, no. 11, pp. 3723–3739, 2019.
[40] G. Ruan, G. Yu, J. Zheng, J. Zou, and S. Yang, “The effect of diversity maintenance on prediction in dynamic multi-objective optimization,” Appl. Soft Comput., vol. 58, pp. 631–647, Sep. 2017. [Online]. Available: https://doi.org/10.1016/j.asoc.2017.05.008
[41] J. Zou, Q. Li, S. Yang, H. Bai, and J. Zheng, “A prediction strategy based on center points and knee points for evolutionary dynamic multi-objective optimization,” Appl. Soft Comput., vol. 61, pp. 806–818, Dec. 2017. [Online]. Available: https://doi.org/10.1016/j.asoc.2017.08.004
[42] A. Zhou, Y. Jin, Q. Zhang, B. Sendhoff, and E. P. K. Tsang, “Prediction-based population re-initialization for evolutionary dynamic multi-objective optimization,” in Proc. 4th Int. Conf. Evol. Multi Criterion Optim. (EMO), Matsushima, Japan, Mar. 2007, pp. 832–846. [Online]. Available: https://doi.org/10.1007/978-3-540-70928-2_62
[43] J. Branke, “Memory enhanced evolutionary algorithms for changing optimization problems,” in Proc. Congr. Evol. Comput. (CEC), vol. 3. Washington, DC, USA, 1999, pp. 1875–1882.
[44] C. K. Goh and K. C. Tan, “A competitive-cooperative coevolutionary paradigm for dynamic multiobjective optimization,” IEEE Trans. Evol. Comput., vol. 13, no. 1, pp. 103–127, Feb. 2009.
[45] I. Hatzakis and D. Wallace, “Dynamic multi-objective optimization with evolutionary algorithms: A forward-looking approach,” in Proc. 8th Annu. Conf. Genet. Evol. Comput., Seattle, WA, USA, 2006, pp. 1201–1208.
[46] Z. Zhang and S. Qian, “Artificial immune system in dynamic environments solving time-varying non-linear constrained multi-objective problems,” Soft Comput., vol. 15, no. 7, pp. 1333–1349, 2011.
[47] L. T. Bui, Z. Michalewicz, E. Parkinson, and M. B. Abello, “Adaptation in dynamic environments: A case study in mission planning,” IEEE Trans. Evol. Comput., vol. 16, no. 2, pp. 190–209, Apr. 2012.
[48] R. Shang, L. Jiao, Y. Ren, L. Li, and L. Wang, “Quantum immune clonal coevolutionary algorithm for dynamic multiobjective optimization,” Soft Comput., vol. 18, no. 4, pp. 743–756, 2014.
[49] Y. Netzer, T. Wang, A. Coates, A. Bissacco, B. Wu, and A. Y. Ng, “Reading digits in natural images with unsupervised feature learning,” 2011. [Online]. Available: https://ai.google/research/pubs/pub37648
[50] I. Olkin and F. Pukelsheim, “The distance between two random vectors with given dispersion matrices,” Linear Algebra Appl., vol. 48, no. 82, pp. 257–263, Dec. 1982.

你可能感兴趣的:(演化计算)

  • 机器学习与深度学习间关系与区别 ℒℴѵℯ心·动ꦿ໊ོ꫞ 人工智能学习深度学习python
    一、机器学习概述定义机器学习（MachineLearning,ML）是一种通过数据驱动的方法，利用统计学和计算算法来训练模型，使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本，识别其中的模式和规律，从而对新的数据进行判断。其核心在于通过训练过程，让模型不断优化和提升其预测准确性。主要类型1.监督学习（SupervisedLearning）监督学习是指在训练数据集中包含输入
  • ArcGIS栅格计算器常见公式（赋值、0和空值的转换、补充栅格空值） 研学随笔 arcgis经验分享
    我们在使用ArcGIS时通常经常用到栅格计算器，今天主要给大家介绍我日常中经常用到的几个公式，供大家参考学习。将特定值（-9999）赋值为0，例如-9999.Con("raster"==-9999,0,"raster")2.给空值赋予特定的值（如0）Con(IsNull("raster"),0,"raster")3.将特定的栅格值(如1)赋值为空值，其他保留原值SetNull("raster"==
  • 每日一题——第九十题 互联网打工人no1 C语言程序设计每日一练c语言
    题目：判断子串是否与主串匹配#include#include#include//////判断子串是否在主串中匹配//////主串///子串///boolisSubstring(constchar*str,constchar*substr){intlenstr=strlen(str);//计算主串的长度intlenSub=strlen(substr);//计算子串的长度//遍历主字符串，对每个可能得
  • 509. 斐波那契数(每日一题) lzyprime
    lzyprime博客(github)创建时间：2021.01.04qq及邮箱：2383518170leetcode笔记题目描述斐波那契数，通常用F(n)表示，形成的序列称为斐波那契数列。该数列由0和1开始，后面的每一项数字都是前面两项数字的和。也就是：F(0)=0，F(1)=1F(n)=F(n-1)+F(n-2)，其中n>1给你n，请计算F(n)。示例1：输入：2输出：1解释：F(2)=F(1)+
  • 398顺境，逆境 戴骁勇
    2018.11.27周二雾霾最近儿子进入了一段顺境期，今天表现尤其不错。今天的数学测试成绩喜人，没有出现以往的计算错误，整个卷面书写工整，附加题也在规定时间内完成且做对。为迎接体育测试的锻炼有了质的飞跃。坐位体前屈成绩突飞猛进，估测成绩能达到12cm，这和上次测试的零分来比，简直是逆袭。儿子还在不断锻炼和提升，唯恐到时候掉链子。跑步姿势在我的调教下，逐渐正规起来，速度随之也有了提升。今晚测试的50
  • 在一台Ubuntu计算机上构建Hyperledger Fabric网络 落叶无声9 区块链超级账本Hyperledgerfabric区块链ubuntu构建hyperledgerfabric
    在一台Ubuntu计算机上构建HyperledgerFabric网络Hyperledgerfabric是一个开源的区块链应用程序平台，为开发基于区块链的应用程序提供了一个起点。当我们提到HyperledgerFabric网络时，我们指的是使用HyperledgerFabric的正在运行的系统。即使只使用最少数量的组件，部署Fabric网络也不是一件容易的事。Fabric社区创建了一个名为Cello
  • GitHub上克隆项目 bigbig猩猩 github
    从GitHub上克隆项目是一个简单且直接的过程，它允许你将远程仓库中的项目复制到你的本地计算机上，以便进行进一步的开发、测试或学习。以下是一个详细的步骤指南，帮助你从GitHub上克隆项目。一、准备工作1.安装Git在克隆GitHub项目之前，你需要在你的计算机上安装Git工具。Git是一个开源的分布式版本控制系统，用于跟踪和管理代码变更。你可以从Git的官方网站（https://git-scm.
  • Day1笔记-Python简介&标识符和关键字&输入输出 ~在杰难逃~ Pythonpython开发语言大数据数据分析数据挖掘
    大家好，从今天开始呢，杰哥开展一个新的专栏，当然，数据分析部分也会不定时更新的，这个新的专栏主要是讲解一些Python的基础语法和知识，帮助0基础的小伙伴入门和学习Python，感兴趣的小伙伴可以开始认真学习啦！一、Python简介【了解】1.计算机工作原理编程语言就是用来定义计算机程序的形式语言。我们通过编程语言来编写程序代码，再通过语言处理程序执行向计算机发送指令，让计算机完成对应的工作，编程
  • 121. 买卖股票的最佳时机 薄荷糖的味道_fb40
    给定一个数组，它的第i个元素是一支给定股票第i天的价格。如果你最多只允许完成一笔交易（即买入和卖出一支股票），设计一个算法来计算你所能获取的最大利润。注意你不能在买入股票前卖出股票。示例1:输入:[7,1,5,3,6,4]输出:5解释:在第2天（股票价格=1）的时候买入，在第5天（股票价格=6）的时候卖出，最大利润=6-1=5。注意利润不能是7-1=6,因为卖出价格需要大于买入价格。示例2:输入:
  • Redis系列：Geo 类型赋能亿级地图位置计算 Ly768768 redisbootstrap数据库
    1前言我们在篇深刻理解高性能Redis的本质的时候就介绍过Redis的几种基本数据结构，它是基于不同业务场景而设计的：动态字符串(REDIS_STRING)：整数(REDIS_ENCODING_INT)、字符串(REDIS_ENCODING_RAW)双端列表(REDIS_ENCODING_LINKEDLIST)压缩列表(REDIS_ENCODING_ZIPLIST)跳跃表(REDIS_ENCODI
  • k均值聚类算法考试例题_k均值算法(k均值聚类算法计算题) 寻找你83497 k均值聚类算法考试例题
    ?算法：第一步：选K个初始聚类中心，z1(1),z2(1)，…，zK(1)，其中括号内的序号为寻找聚类中心的迭代运算的次序号。聚类中心的向量值可任意设定，例如可选开始的K个.k均值聚类：---------一种硬聚类算法，隶属度只有两个取值0或1，提出的基本根据是“类内误差平方和最小化”准则；模糊的c均值聚类算法：--------一种模糊聚类算法，是.K均值聚类算法是先随机选取K个对象作为初始的聚类
  • Python开发常用的三方模块如下： 换个网名有点难 python开发语言
    Python是一门功能强大的编程语言，拥有丰富的第三方库，这些库为开发者提供了极大的便利。以下是100个常用的Python库，涵盖了多个领域：1、NumPy，用于科学计算的基础库。2、Pandas，提供数据结构和数据分析工具。3、Matplotlib，一个绘图库。4、Scikit-learn，机器学习库。5、SciPy，用于数学、科学和工程的库。6、TensorFlow，由Google开发的开源机
  • Shell、Bash、Zsh这都是啥啊 小白码上飞 bashlinux开发语言
    Zsh和Bash都是我们常用的Shell，那先搞明白啥是shell吧。Shell作为一个单词，他是“壳”的意思，蛋壳坚果壳。之所以叫壳，是为了和计算机的“核”来区分，用它表示“为使用者提供的操作界面”。所以这个命名其实很形象，翻译成中文，直译过来叫“壳层”。个人认为这个叫法很奇怪，意译貌似也没有什么好的词汇来匹配。就还是叫shell吧。维基百科给的定义是：Incomputing,ashellisa
  • ExpRe[25] bash外的其它shell：zsh和fish tritone ExpRebashlinuxubuntushell
    文章目录zsh基础配置实用特性插件`autojump`语法高亮自动补全fish优点缺点时效性本篇撰写时间为2021.12.15，由于计算机技术日新月异，博客中所有内容都有时效和版本限制，具体做法不一定总行得通，链接可能改动失效，各种软件的用法可能有修改。但是其中透露的思想往往是值得学习的。本篇前置：ExpRe[10]Ubuntu[2]准备神秘软件、备份恢复软件https://www.cnblogs
  • 简单了解 JVM 记得开心一点啊 jvm
    目录♫什么是JVM♫JVM的运行流程♫JVM运行时数据区♪虚拟机栈♪本地方法栈♪堆♪程序计数器♪方法区/元数据区♫类加载的过程♫双亲委派模型♫垃圾回收机制♫什么是JVMJVM是JavaVirtualMachine的简称，意为Java虚拟机。虚拟机是指通过软件模拟的具有完整硬件功能的、运行在一个完全隔离的环境中的完整计算机系统（如：JVM、VMwave、VirtualBox）。JVM和其他两个虚拟机
  • 数据结构 | 栈和队列 TT-Kun 数据结构与算法数据结构栈队列C语言
    文章目录栈和队列1.栈：后进先出（LIFO）的数据结构1.1概念与结构1.2栈的实现2.队列：先进先出（FIFO）的数据结构2.1概念与结构2.2队列的实现3.栈和队列算法题3.1有效的括号3.2用队列实现栈3.3用栈实现队列3.4设计循环队列结论栈和队列在计算机科学中，栈和队列是两种基本且重要的数据结构，它们在处理数据存储和访问顺序方面有着独特的规则和应用。本文将详细介绍栈和队列的概念、结构、实
  • Python神器！WEB自动化测试集成工具 DrissionPage 亚丁号 python开发语言
    一、前言用requests做数据采集面对要登录的网站时，要分析数据包、JS源码，构造复杂的请求，往往还要应付验证码、JS混淆、签名参数等反爬手段，门槛较高。若数据是由JS计算生成的，还须重现计算过程，体验不好，开发效率不高。使用浏览器，可以很大程度上绕过这些坑，但浏览器运行效率不高。因此，这个库设计初衷，是将它们合而为一，能够在不同须要时切换相应模式，并提供一种人性化的使用方法，提高开发和运行效率
  • 计算机木马详细编写思路 小熊同学哦 php开发语言木马木马思路
    导语：计算机木马（ComputerTrojan）是一种恶意软件，通过欺骗用户从而获取系统控制权限，给黑客打开系统后门的一种手段。虽然木马的存在给用户和系统带来严重的安全风险，但是了解它的工作原理与编写思路，对于我们提高防范意识、构建更健壮的网络安全体系具有重要意义。本篇博客将深入剖析计算机木马的详细编写思路，以及如何复杂化挑战，以期提高读者对计算机木马的认识和对抗能力。计算机木马的基本原理计算机木
  • 4 大低成本娱乐方式: 小说, 音乐, 视频, 电子游戏 穷人小水滴 娱乐音视频低成本小说游戏
    穷人如何获得快乐?小说,音乐,视频,游戏,本文简单盘点一下这4大低成本(安全)娱乐方式.这里是穷人小水滴,专注于穷人友好型低成本技术.(本文为58号作品.)目录1娱乐方式1.1小说(网络小说)1.2音乐1.3视频(b站)1.4游戏(电子游戏/计算机软件)2低成本:一只手机即可3总结与展望1娱乐方式这几种,也可以说是艺术的具体形式.更专业的说,(娱乐)是劳动力再生产的重要组成部分.使人放松,获得快乐
  • 计算机网络八股总结 Petrichorzncu 八股总结计算机网络笔记
    这里写目录标题网络模型划分（五层和七层）及每一层的功能五层网络模型七层网络模型（OSI模型）==三次握手和四次挥手具体过程及原因==三次握手四次挥手TCP/IP协议组成==UDP协议与TCP/IP协议的区别==Http协议相关知识网络地址，子网掩码等相关计算网络模型划分（五层和七层）及每一层的功能五层网络模型应用层：负责处理网络应用程序，如电子邮件、文件传输和网页浏览。主要协议包括HTTP、FTP
  • matlab delsat = setdiff(1:69,unique(Eph(30,:)))； 语句含义 黄卷青灯77 matlab开发语言setdiff
    这行MATLAB代码用于计算在范围1:69中不包含在Eph矩阵第30行的唯一值集合中的所有元素。具体解释如下：delsat=setdiff(1:69,unique(Eph(30,:)));解释Eph(30,:)Eph(30,:)提取矩阵Eph的第30行的所有列元素。这是一个行向量，包含了第30行的所有值。unique(Eph(30,:))unique函数返回Eph(30,:)中的唯一元素。这意味着
  • #千锋逆战班 郭燕 学习的一天开启 郭千岁呗
    在千锋"逆战"学习云计算第17天加油努力会有好结果复习昨天知识中国加油！武汉加油！千峰加油!我自己加油！
  • 计算机毕业设计PHP仓储综合管理系统（源码+程序+VUE+lw+部署） java毕设程序源码王哥 php课程设计vue.js
    该项目含有源码、文档、程序、数据库、配套开发软件、软件安装教程。欢迎交流项目运行环境配置：phpStudy+Vscode+Mysql5.7+HBuilderX+Navicat11+Vue+Express。项目技术：原生PHP++Vue等等组成，B/S模式+Vscode管理+前后端分离等等。环境需要1.运行环境：最好是小皮phpstudy最新版，我们在这个版本上开发的。其他版本理论上也可以。2.开发
  • 经纬恒润二面&三七互娱一面&元象二面 Redstone Monstrosity 面试前端
    1.请尽可能详细地说明，进程和线程的区别，分别有哪些应用场景？进程间如何通信？线程间如何通信？你的回答中不要写出示例代码。进程和线程是操作系统中的两个基本概念，它们在计算机系统中扮演着不同的角色，并且在不同的应用场景中发挥作用。进程和线程的区别定义：进程：进程是操作系统进行资源分配和调度的基本单位。每个进程都有独立的内存空间和系统资源。线程：线程是进程内的一个执行单元，是操作系统进行调度的最小单位
  • AI大模型的架构演进与最新发展 季风泯灭的季节 AI大模型应用技术二人工智能架构
    随着深度学习的发展，AI大模型（LargeLanguageModels,LLMs）在自然语言处理、计算机视觉等领域取得了革命性的进展。本文将详细探讨AI大模型的架构演进，包括从Transformer的提出到GPT、BERT、T5等模型的历史演变，并探讨这些模型的技术细节及其在现代人工智能中的核心作用。一、基础模型介绍：Transformer的核心原理Transformer架构的背景在Transfo
  • 孕妈必备：怀孕第一周孕妈和准爸爸需要知道的那些事儿 张女子育儿
    对于新婚夫妻来说，怀孕第一周准妈妈和准爸爸都会感觉到既惊喜又有点不知所措吧！怀孕第一周孕妈有什么反应，怀孕第一周孕妈需要注意的事情有哪些呢？准爸爸又该如何照顾孕妇及其为孩子做些什么呢？今日小编就和大家说说怀孕第一周的诸多问题，让孕妈和准爸爸做好准备。怀孕第一周该如何计算呢？人们通常都说准妈妈要“怀胎10月”，但实际上按照阳历计算的话，胎儿在妈妈子宫内生活的时间是没有10个月的。准妈妈得知自己怀孕，
  • 【Java】已解决：java.util.concurrent.CompletionException 屿小夏 java开发语言
    文章目录一、分析问题背景出现问题的场景代码片段二、可能出错的原因三、错误代码示例四、正确代码示例五、注意事项已解决：java.util.concurrent.CompletionException一、分析问题背景在Java并发编程中，java.util.concurrent.CompletionException是一种常见的运行时异常，通常在使用CompletableFuture进行异步计算时出现
  • 【加密算法基础——对称加密和非对称加密】 XWWW668899 网络安全服务器笔记
    对称加密与非对称加密对称加密和非对称加密是两种基本的加密方法，各自有不同的特点和用途。以下是详细比较：1.对称加密特点密钥:使用相同的密钥进行加密和解密。发送方和接收方必须共享这个密钥。速度:通常速度较快，适合处理大量数据。实现:算法相对简单，计算效率高。常见算法AES(高级加密标准)DES(数据加密标准)3DES(三重数据加密标准)RC4(流密码)应用场景文件加密磁盘加密传输大量数据时的加密2.
  • 信息系统安全相关概念(上) YuanDaima2048 课程笔记基础概念安全信息安全笔记
    文章总览：YuanDaiMa2048博客文章总览下篇:信息系统安全相关概念(下)信息系统安全相关概念[上]信息系统概述信息系统信息系统架构信息系统发展趋势：信息系统日趋大型化、复杂化信息系统面临的安全威胁信息系统安全架构设计--以云计算为例信息系统安全需求及安全策略自主访问控制策略DAC强制访问控制策略MAC信息系统概述信息系统用于收集、存储和处理数据以及传递信息、知识和数字产品的一组集成组件。几
  • 【2023年】云计算金砖牛刀小试6 geekgold 云计算服务器网络kubernetes容器
    第一套【任务1】私有云服务搭建[10分]【题目1】基础环境配置[0.5分]使用提供的用户名密码，登录提供的OpenStack私有云平台，在当前租户下，使用CentOS7.9镜像，创建两台云主机，云主机类型使用4vCPU/12G/100G_50G类型。当前租户下默认存在一张网卡，自行创建第二张网卡并连接至controller和compute节点（第二张网卡的网段为10.10.X.0/24，X为工位号
  • 二分查找排序算法 周凡杨 java二分查找排序算法折半
    一：概念 二分查找又称 折半查找（ 折半搜索/ 二分搜索），优点是比较次数少，查找速度快，平均性能好；其缺点是要求待查表为有序表，且插入删除困难。因此，折半查找方法适用于不经常变动而 查找频繁的有序列表。首先，假设表中元素是按升序排列，将表中间位置记录的关键字与查找关键字比较，如果两者相等，则查找成功；否则利用中间位置记录将表 分成前、后两个子表，如果中间位置记录的关键字大于查找关键字，则进一步
  • java中的BigDecimal bijian1013 javaBigDecimal
            在项目开发过程中出现精度丢失问题，查资料用BigDecimal解决，并发现如下这篇BigDecimal的解决问题的思路和方法很值得学习，特转载。         原文地址：http://blog.csdn.net/ugg/article/de
  • Shell echo命令详解 daizj echoshell
    Shell echo命令 Shell 的 echo 指令与 PHP 的 echo 指令类似，都是用于字符串的输出。命令格式： echo string 您可以使用echo实现更复杂的输出格式控制。 1.显示普通字符串: echo "It is a test" 这里的双引号完全可以省略，以下命令与上面实例效果一致： echo Itis a test 2.显示转义
  • Oracle DBA 简单操作 周凡杨 oracle dba sql
    --执行次数多的SQL select sql_text,executions from (      select sql_text,executions from v$sqlarea order by executions desc      ) where rownum<81;  &nb
  • 画图重绘 朱辉辉33 游戏
      我第一次接触重绘是编写五子棋小游戏的时候，因为游戏里的棋盘是用线绘制的，而这些东西并不在系统自带的重绘里，所以在移动窗体时，棋盘并不会重绘出来。所以我们要重写系统的重绘方法。   在重写系统重绘方法时，我们要注意一定要调用父类的重绘方法，即加上super.paint(g)，因为如果不调用父类的重绘方式，重写后会把父类的重绘覆盖掉，而父类的重绘方法是绘制画布，这样就导致我们
  • 线程之初体验 西蜀石兰 线程
    一直觉得多线程是学Java的一个分水岭，懂多线程才算入门。 之前看《编程思想》的多线程章节，看的云里雾里，知道线程类有哪几个方法，却依旧不知道线程到底是什么？书上都写线程是进程的模块，共享线程的资源，可是这跟多线程编程有毛线的关系，呜呜。。。 线程其实也是用户自定义的任务，不要过多的强调线程的属性，而忽略了线程最基本的属性。 你可以在线程类的run()方法中定义自己的任务，就跟正常的Ja
  • linux集群互相免登陆配置 林鹤霄 linux
    配置ssh免登陆 1、生成秘钥和公钥    ssh-keygen -t rsa 2、提示让你输入，什么都不输，三次回车之后会在~下面的.ssh文件夹中多出两个文件id_rsa 和 id_rsa.pub    其中id_rsa为秘钥，id_rsa.pub为公钥，使用公钥加密的数据只有私钥才能对这些数据解密    c
  • mysql : Lock wait timeout exceeded; try restarting transaction aigo mysql
    原文：http://www.cnblogs.com/freeliver54/archive/2010/09/30/1839042.html   原因是你使用的InnoDB   表类型的时候, 默认参数:innodb_lock_wait_timeout设置锁等待的时间是50s, 因为有的锁等待超过了这个时间,所以抱错.   你可以把这个时间加长,或者优化存储
  • Socket编程 基本的聊天实现。 alleni123 socket
    public class Server { //用来存储所有连接上来的客户 private List<ServerThread> clients; public static void main(String[] args) { Server s = new Server(); s.startServer(9988); } publi
  • 多线程监听器事件模式(一个简单的例子) 百合不是茶 线程监听模式
        多线程的事件监听器模式   监听器时间模式经常与多线程使用,在多线程中如何知道我的线程正在执行那什么内容,可以通过时间监听器模式得到        创建多线程的事件监听器模式 思路:    1, 创建线程并启动,在创建线程的位置设置一个标记     2,创建队
  • spring InitializingBean接口 bijian1013 javaspring
    spring的事务的TransactionTemplate，其源码如下： public class TransactionTemplate extends DefaultTransactionDefinition implements TransactionOperations, InitializingBean{ ... } TransactionTemplate继承了DefaultT
  • Oracle中询表的权限被授予给了哪些用户 bijian1013 oracle数据库权限
            Oracle查询表将权限赋给了哪些用户的SQL，以备查用。 select t.table_name as "表名", t.grantee as "被授权的属组", t.owner as "对象所在的属组"
  • 【Struts2五】Struts2 参数传值 bit1129 struts2
    Struts2中参数传值的3种情况 1.请求参数绑定到Action的实例字段上 2.Action将值传递到转发的视图上 3.Action将值传递到重定向的视图上   一、请求参数绑定到Action的实例字段上以及Action将值传递到转发的视图上 Struts可以自动将请求URL中的请求参数或者表单提交的参数绑定到Action定义的实例字段上，绑定的规则使用ognl表达式语言
  • 【Kafka十四】关于auto.offset.reset[Q/A] bit1129 kafka
    I got serveral questions about  auto.offset.reset. This configuration parameter governs how  consumer read the message from  Kafka when  there is no initial offset in ZooKeeper or
  • nginx gzip压缩配置 ronin47 nginx gzip 压缩范例
    nginx gzip压缩配置 更多 0 nginx gzip 配置   随着nginx的发展，越来越多的网站使用nginx，因此nginx的优化变得越来越重要，今天我们来看看nginx的gzip压缩到底是怎么压缩的呢？ gzip(GNU-ZIP)是一种压缩技术。经过gzip压缩后页面大小可以变为原来的30%甚至更小，这样，用
  • java-13.输入一个单向链表，输出该链表中倒数第 k 个节点 bylijinnan java
    two cursors. Make the first cursor go K steps first. /* * 第 13 题：题目：输入一个单向链表，输出该链表中倒数第 k 个节点 */ public void displayKthItemsBackWard(ListNode head,int k){ ListNode p1=head,p2=head;
  • Spring源码学习-JdbcTemplate queryForObject bylijinnan javaspring
    JdbcTemplate中有两个可能会混淆的queryForObject方法： 1. Object queryForObject(String sql, Object[] args, Class requiredType) 2. Object queryForObject(String sql, Object[] args, RowMapper rowMapper) 第1个方法是只查
  • [冰川时代]在冰川时代,我们需要什么样的技术? comsci 技术
         看美国那边的气候情况....我有个感觉...是不是要进入小冰期了?      那么在小冰期里面...我们的户外活动肯定会出现很多问题...在室内呆着的情况会非常多...怎么在室内呆着而不发闷...怎么用最低的电力保证室内的温度.....这都需要技术手段...   &nb
  • js 获取浏览器型号 cuityang js浏览器
    根据浏览器获取iphone和apk的下载地址 <!DOCTYPE html> <html> <head>     <meta charset="utf-8" content="text/html"/>     <meta name=
  • C# socks5详解 转 dalan_123 socketC#
    http://www.cnblogs.com/zhujiechang/archive/2008/10/21/1316308.html  这里主要讲的是用.NET实现基于Socket5下面的代理协议进行客户端的通讯，Socket4的实现是类似的，注意的事，这里不是讲用C#实现一个代理服务器，因为实现一个代理服务器需要实现很多协议，头大，而且现在市面上有很多现成的代理服务器用，性能又好，
  • 运维 Centos问题汇总 dcj3sjt126com 云主机
    一、sh 脚本不执行的原因 sh脚本不执行的原因 只有2个 1.权限不够 2.sh脚本里路径没写完整。   二、解决You have new mail in /var/spool/mail/root 修改/usr/share/logwatch/default.conf/logwatch.conf配置文件 MailTo = MailFrom   三、查询连接数
  • Yii防注入攻击笔记 dcj3sjt126com sqlWEB安全yii
    网站表单有注入漏洞须对所有用户输入的内容进行个过滤和检查，可以使用正则表达式或者直接输入字符判断，大部分是只允许输入字母和数字的，其它字符度不允许；对于内容复杂表单的内容，应该对html和script的符号进行转义替换：尤其是<,>,',"",&这几个符号 这里有个转义对照表： http://blog.csdn.net/xinzhu1990/articl
  • MongoDB简介[一] eksliang mongodbMongoDB简介
    MongoDB简介 转载请出自出处：http://eksliang.iteye.com/blog/2173288 1.1易于使用        MongoDB是一个面向文档的数据库，而不是关系型数据库。与关系型数据库相比，面向文档的数据库不再有行的概念，取而代之的是更为灵活的“文档”模型。        另外，不
  • zookeeper windows 入门安装和测试 greemranqq zookeeper安装分布式
    一、序言       以下是我对zookeeper 的一些理解：      zookeeper 作为一个服务注册信息存储的管理工具，好吧，这样说得很抽象，我们举个“栗子”。       栗子1号：       假设我是一家KTV的老板，我同时拥有5家KTV，我肯定得时刻监视
  • Spring之使用事务缘由(2-注解实现) ihuning spring
      Spring事务注解实现   1. 依赖包：     1.1 spring包：           spring-beans-4.0.0.RELEASE.jar           spring-context-4.0.0.
  • iOS App Launch Option 啸笑天 option
    iOS 程序启动时总会调用application:didFinishLaunchingWithOptions:，其中第二个参数launchOptions为NSDictionary类型的对象，里面存储有此程序启动的原因。   launchOptions中的可能键值见UIApplication Class Reference的Launch Options Keys节 。 1、若用户直接
  • jdk与jre的区别（_） macroli javajvmjdk
    简单的说JDK是面向开发人员使用的SDK，它提供了Java的开发环境和运行环境。SDK是Software Development Kit 一般指软件开发包，可以包括函数库、编译程序等。  JDK就是Java Development Kit JRE是Java Runtime Enviroment是指Java的运行环境，是面向Java程序的使用者，而不是开发者。 如果安装了JDK，会发同你
  • Updates were rejected because the tip of your current branch is behind qiaolevip 学习永无止境每天进步一点点众观千象git
    $ git push joe prod-2295-1 To [email protected]:joe.le/dr-frontend.git ! [rejected] prod-2295-1 -> prod-2295-1 (non-fast-forward) error: failed to push some refs to '[email protected]
  • [一起学Hive]之十四-Hive的元数据表结构详解 superlxw1234 hivehive元数据结构
    关键字：Hive元数据、Hive元数据表结构   之前在 “[一起学Hive]之一–Hive概述，Hive是什么”中介绍过，Hive自己维护了一套元数据，用户通过HQL查询时候，Hive首先需要结合元数据，将HQL翻译成MapReduce去执行。 本文介绍一下Hive元数据中重要的一些表结构及用途，以Hive0.13为例。   文章最后面，会以一个示例来全面了解一下，
  • Spring 3.2.14，4.1.7，4.2.RC2发布 wiselyman Spring 3
      Spring 3.2.14、4.1.7及4.2.RC2于6月30日发布。   其中Spring 3.2.1是一个维护版本(维护周期到2016-12-31截止)，后续会继续根据需求和bug发布维护版本。此时，Spring官方强烈建议升级Spring框架至4.1.7 或者将要发布的4.2 。   其中Spring 4.1.7主要包含这些更新内容。
按字母分类： ABCDEFGHIJKLMNOPQRSTUVWXYZ其他