数据结构与算法11——排序算法汇总（C语言代码）

数据结构与算法11——排序算法汇总（C语言代码）

 

1、排序的方法及比较。堆的定义

 

目录

数据结构与算法11——排序算法汇总（C语言代码）

1、排序的方法及比较。堆的定义

1.1 排序算法优劣的判断标准

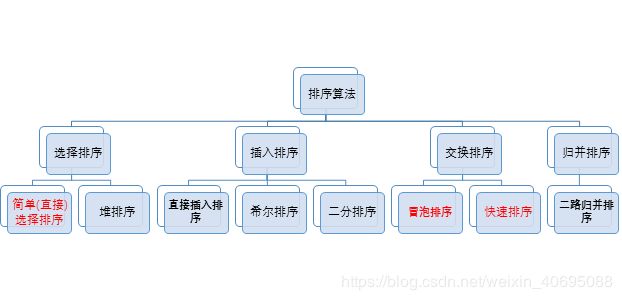
1.2排序算法的分类

1.3各种算法的思想及实例

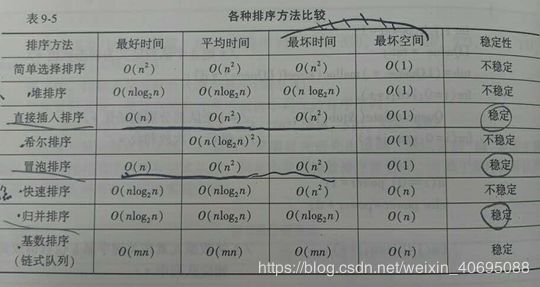
1.4各种算法的性能比较

---

1.1 排序算法优劣的判断标准

1.2排序算法的分类

1.3各种算法的思想及实例

1) 直接选择排序算法

思想：第一趟：从n个元素中找出关键字最小的记录放在第一个位置

           第二趟：从元素集合的2~n个元素中找出最小关键记录放在第二个位置

           第三趟：从元素集合的3~n个元素中找出最小关键记录放在第三个位置

以此类推直到全部遍历：

  要求写出代码：

int i,j,pos;int temp;
int a[];      //存放n个无序元素的数组
for(i=0;i

算法评价：直接选择排序共需n-1次选择，每次选择要进行n-i次比较，所以算法的比较次数为C=(n^2-n)/2，时间复杂度为O(n^2)，算法不稳定。原始数据越有序，需要移动元素的次数越小，选择单链表的存储方式，因为要经常交换元素。

2) 堆排序算法

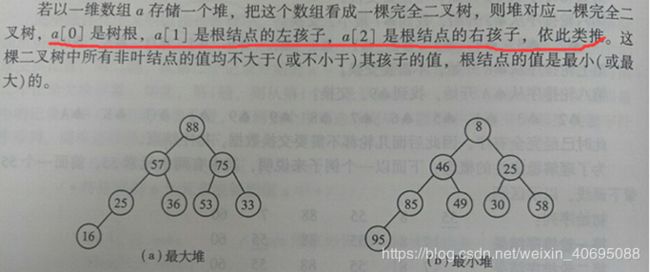
   堆的定义：

   思想：第一步：把无序的n个元素建成一个完全二叉树

              第二步：调整完全二叉树为小根堆或大根堆

              第三步：输出堆顶元素，调整剩下的元素

              第四步：循环直至所有元素输出

实例：

算法评价：

• 1、在堆排序中共需进行n[n/2]-1次筛选
• 2、每次输出堆顶元素进行调整时的时间复杂度平均是O(log2 n)，对n各节点进行堆排序的时间复杂度为O(nlog2 n),空间复杂度为O(1)
• 3.要求从小到大排序则建立最大堆，要从大到小排序则建立最小堆
• 4.可以用顺序存储创建堆

3) 直接插入排序算法

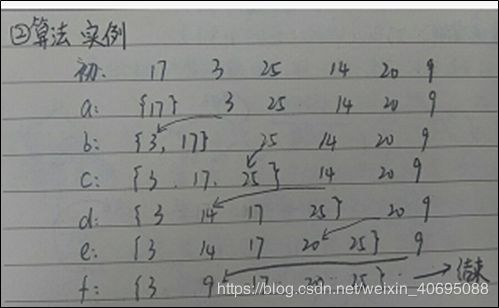
   思想：第一步：对n个元素假定以第一个元素是有序序列，比较a[0],a[1]进行排序，形成{a[0],a[1]}的一个有序序列

              第二步：再将a[2]与{a[0],a[1]}进行排序，形成有序序列{a[0],a[1],a[2]}

              以此类推，直至找出包含所有元素的有序序列{……..}

b算作第一趟，c算作第二趟,共需进行n-1趟排序

 算法评价：1、最好情况下：总比较次数:n-1，总移动次数2(n-1)，时间复杂度O(n)

                  2、最坏情况，总比较次数:(n-1)(n-2)/2，总移动次数(n-1)(n-4)/2，时间复杂度O(n^2)

                  3、平均情况下，时间复杂度为O(n^2)，空间复杂度为O(1)，算法稳定

                  4.原始数据越有序，比较次数越少，更适合有序数据，是稳定排序算法

4) 希尔排序算法

思想：第一步：先把n个元素分成若干组，选择步长序列t1,t2…tk,t1=n/2,…tk=1

      第二步：将原序列分成若干个序列，分别对各子序列进行直接插入排序

实例：

算法评价：时间复杂度O(n(log2 n)^2),空间复杂度O(1),不稳定

希尔排序是强力版的直接插入排序，元素数n越大，算法的优势越明显，需要知道元素的位置，不能使用链式存储结构，适用于顺序存储。

5) 冒泡排序算法

两两比较，调整顺序，a[0]与a[1]比再调整，a[1]与a[2]比再调整，a[2]与a[3]比再调整，以此类推，比到结尾就是一轮。

算法适用于无序的数据，比较次数与原始数据的有序性无关，可以顺序存储也可以链式存储。

  算法评价：

• 1、最好的情况是原始数据有序，循环n-1次，不发生交换，时间复杂度为O(n)，最坏的时间复杂度为O(n^2)
• 2、空间复杂度为O(1)
• 3、冒泡排序是稳定的排序算法之一。三个常见排序算法中稳定的算法是：冒泡排序，直接插入排序，归并排序。
•  4、最好的情况是原序列有序，则只需要扫描一次，时间复杂度是O(n),最坏的情况是要比较n-1次，时间复杂度是O(n^2)
•  

 例题：

要求会写算法代码：

int a[],i,j;
tag=1;
for(i=1;i

6) 快速排序算法

适用于顺序存储，方便存储元素，不适合链式存储，因为单链表只能从开头逐渐遍历到某个位置，不能直接查找某一个具体的元素。

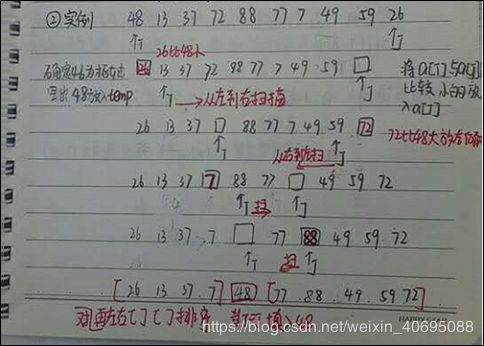
算法思想：（1）选取一个标准元素（通常是第一个元素——枢轴）

                  （2）在序列的右端开始扫描，遇到比a[0]小的元素a[j]则放到a[0]的位置，再从左端开始扫描，遇到比a[0]大的元素                                 则放到a[j]的位置，以此类推直至i=j

                  （3）当左右指针i和j指向同一个位置时放入枢轴元素

                  （4）采用同样的方法对枢轴的左右子序列进行快速排序

算法代码：

void  QuickSort(int a[],int low,int high){
int i=low,j=higt,temp;
temp=a[low];
while(i

算法评价：快速排序不稳定。时间复杂度为O(nlog2 n)，最坏的时间复杂度为O(n^2)

7) 二路归并排序算法

1.4各种算法的性能比较

2、排序算法比较代码（C语言）

/* 直接插入排序的算法源程序*/

#include
#include 
#include 
#define MAXNUM 50000

typedef int KeyType;
typedef int DataType;
typedef struct {
    KeyType key;       /* 排序码字段 */
    /*DataType info;           记录的其它字段 */
} RecordNode;

typedef struct {
    int n;               /* n为文件中的记录个数，nrecord;

    for( i = 1; i < pvector->n; i++ ) { /* 依次插入记录R1, R2…Rn-1 */
        temp = data[i]; 
        for ( j = i-1; temp.key < data[j].key && j >= 0; j-- )
            /* 由后向前找插入位置 将排序码大于ki的记录后移 */
            data[j+1] = data[j];
        if( j != i-1 ) data[j+1] = temp;
    }
}
void  shellSort(SortObject * pvector, int d) {	/* 按递增序进行Shell排序 */
    int i, j, inc; 
    RecordNode temp, *data = pvector->record;
    
    for (inc = d; inc > 0; inc /= 2) {
        /* inc 为本趟shell排序增量 */
        for (i = inc; i < pvector->n; i++) { 
            temp = data[i];          	/* 保存待插入记录Ri*/ 
            for (j = i-inc; j >= 0 && temp.key < data[j].key; j -= inc)
                data[j+inc] = data[j];	/* 查找插入位置，记录后移 */
            data[j+inc] = temp;			/* 插入记录Ri */
        }
    }
}
void quickSort(SortObject * pvector, int l, int r) {
    int i, j;
    RecordNode temp, *data = pvector->record;
    
    if (l >= r) return;   /* 只有一个记录或无记录，则无须排序 */

    i = l;  j = r;  temp = data[i];

    while (i != j) {        /* 寻找Rl的最终位置 */
        while( data[j].key >= temp.key && j > i )
            j--;         /* 从右向左扫描，查找第1个排序码小于temp.key的记录 */
        if (i < j) data[i++] = data[j];   

        while( data[i].key <= temp.key && j > i )
            i++;         /* 从左向右扫描，查找第1个排序码大于temp.key的记录 */
        if (i < j) data[j--] = data[i];
    }

    data[i] = temp;                 /* 找到Rl的最终位置 */
    quickSort(pvector, l, i-1);                 /* 递归处理左区间 */
    quickSort(pvector, i+1, r);            /* 递归处理右区间 */
}
#define leftChild(i) (2*(i)+1)

void  sift(SortObject * pvector, int i, int n) {
    int child; 
    RecordNode temp = pvector->record[i], *data = pvector->record;

    child = leftChild(i);      /* Rchild是R0的左子女 */
    while(childn;
    RecordNode temp, *data = pvector->record;
    
    for (i = n/2-1; i >= 0; i--)
        sift(pvector, i, n);              /* 建立初始堆 */
    for (i = n-1; i > 0; i--) {           /* 进行n-1趟堆排序 */
        temp = data[0];                   /* 当前堆顶记录和最后一个记录互换 */
        data[0] = data[i];
        data[i] = temp;
        sift(pvector, 0, i);              /* 从R0到Ri-1重建堆 */
    }
}

int main(){
	int num;
	int b[5000];
	SortObject vector;
	printf("请输入你想要的数据的长度：");
	scanf("%d",&num);
	 vector.n=num;
    for (long a=0; a