数据结构与算法(python版)之树
数据结构与算法(python版)之树
- 一、什么是树
- 二、树结构的相关术语(11个)
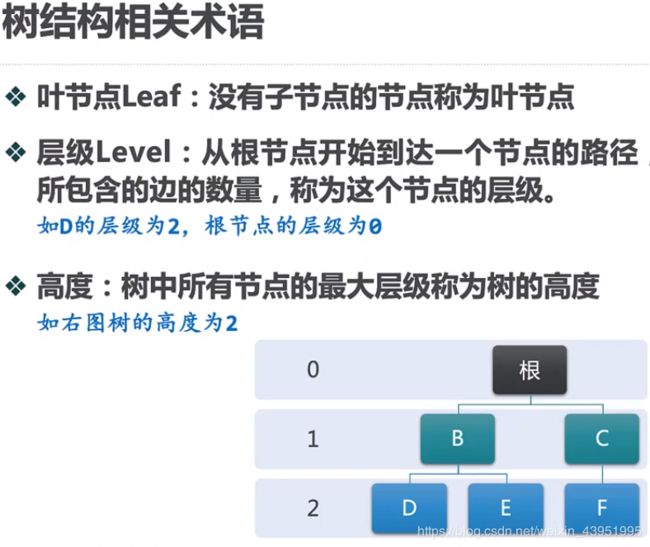
- 1.相关术语
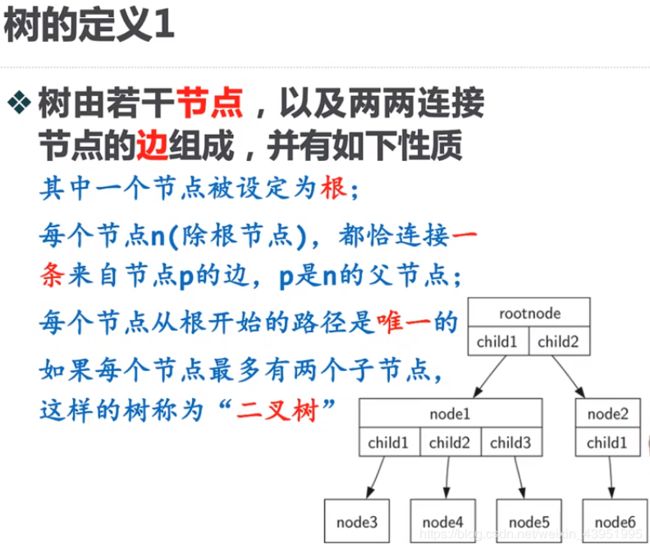
- 2.树的定义1
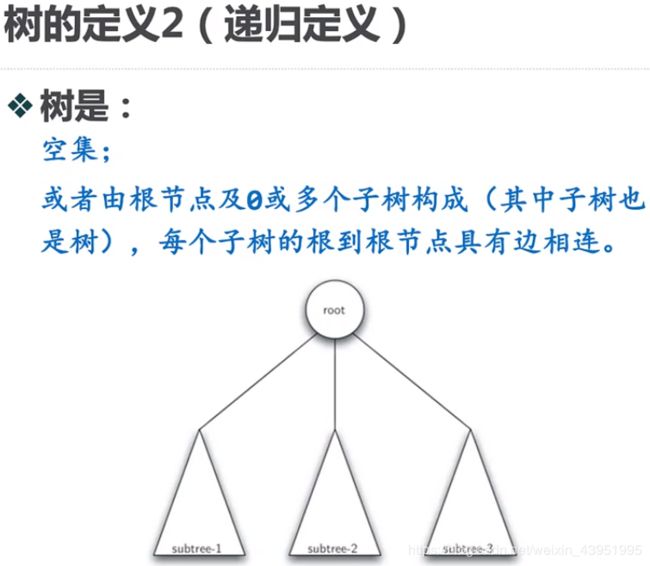
- 3.树的定义2
- 三、树的嵌套列表实现
- 四、树的链表实现
- 五、树的应用:表达式解析
- 1.表达式解析
- 2.建立表达式解析树
- 3.利用表达式解析树求值
- 六、树的遍历
- 1.树的遍历
- 2.遍历程序
- 4.遍历示例
- 七、优先队列和二叉堆
- 1.优先队列
- 2.二叉堆实现优先队列
- 3.用非嵌套列表实现二叉堆
- 4.堆次序
- 3.二叉堆的python实现
- 八、二叉查找树及操作
- 1.二叉查找树
- 2.二叉查找树的实现
- 九、AVL树
- 十、小结
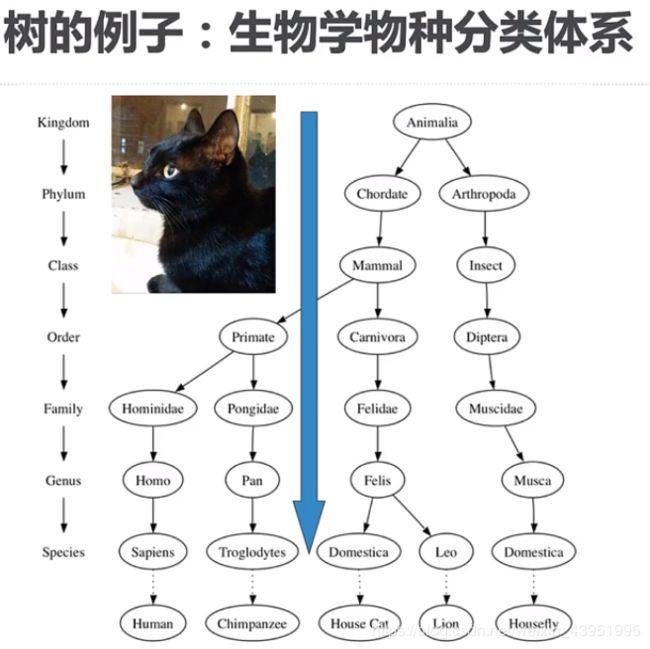
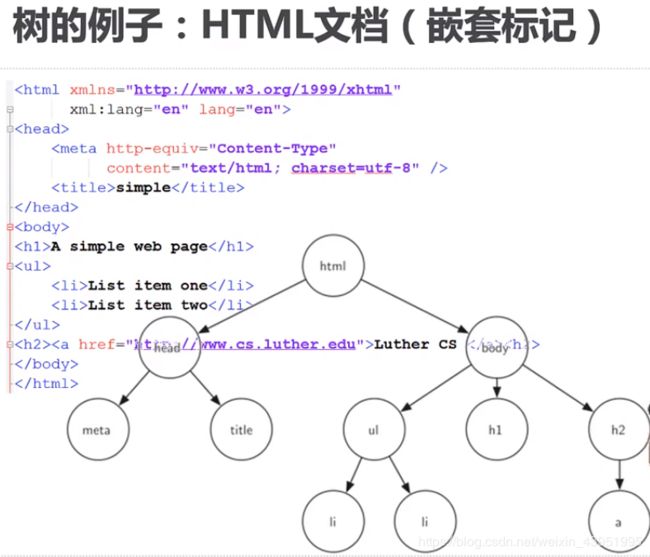
一、什么是树
二、树结构的相关术语(11个)
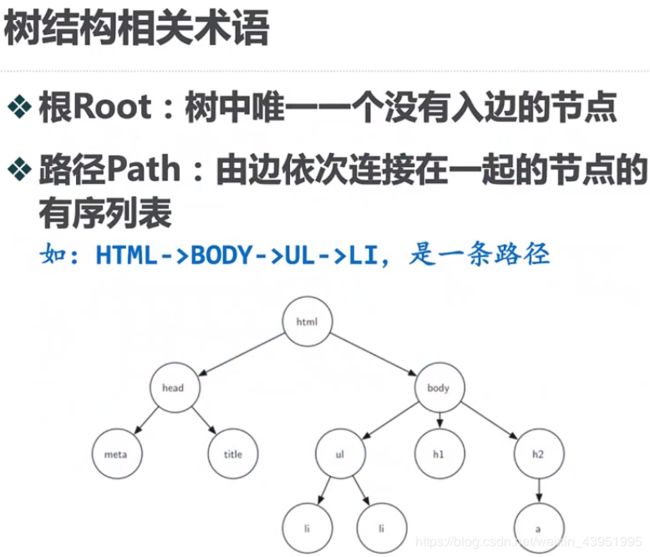
1.相关术语
2.树的定义1
3.树的定义2
三、树的嵌套列表实现
def BinaryTree(r):
return [r,[],[]]
def insertLeft(root,newBranch):
t=root.pop(1)
if len(t)>1:
root.insert(1,[newBranch,t,[]])
else:
root.insert(1,[newBranch,[],[]])
return root
def insertRight(root,newBranch):
t=root.pop(2)
if len(t)>1:
root.insert(2,[newBranch,[],t])
else:
root.insert(2,[newBranch,[],[]])
return root
def getRootValue(root):
return root[0]
def setRootValue(root,newVal):
root[0]=newVal
def getLeftChild(root):
return root[1]
def getRightChild(root):
return root[2]
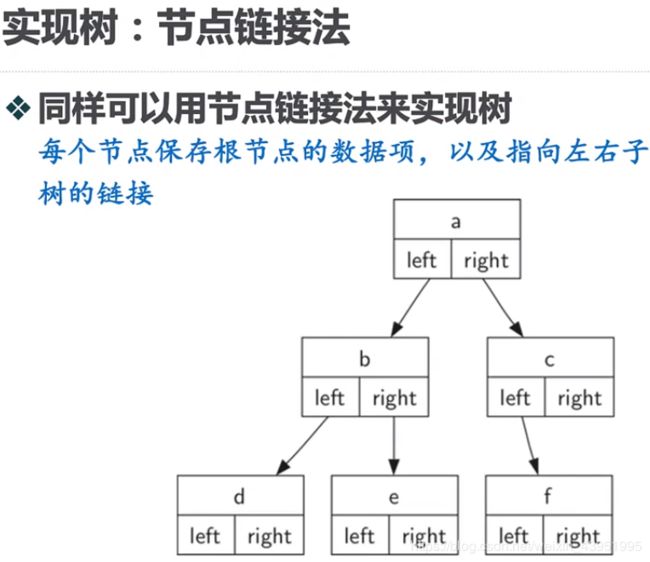
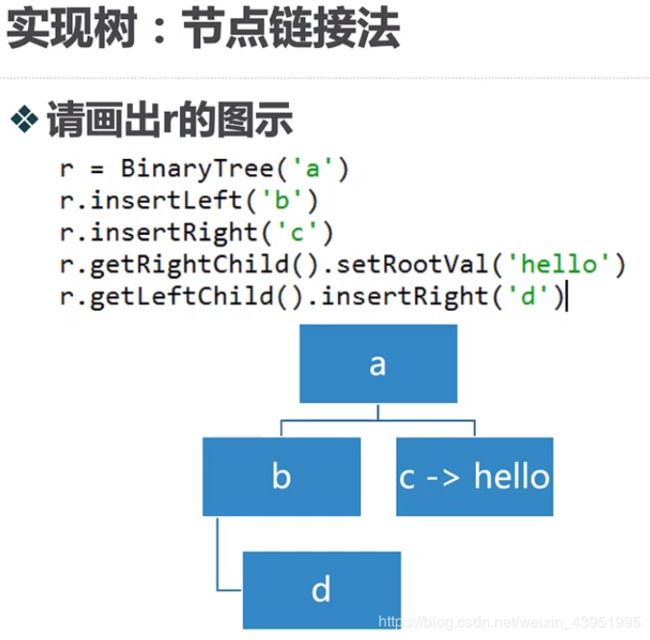
四、树的链表实现
class BinaryTree:
def __init__(self,rootObj):
self.key=rootObj
self.leftChild=None
self.rightChild=None
def insertLeft(self,newNode):
if self.leftChild==None:
self.leftChild=BinaryTree(newNode)
else:
temp=BinaryTree(newNode)
temp.leftChild=self.leftChild
self.leftChild=temp
def insertRight(self,newNode):
if self.rightChild==None:
self.rightChild=BinaryTree(newNode)
else:
temp=BinaryTree(newNode)
temp.rightChild=self.rightChild
self.rightChild=temp
def getRightChild(self):
return self.rightChild
def getLeftChild(self):
return self.leftChild
def getRootVal(self):
return self.key
def setRootVal(self,obj):
self.key=obj
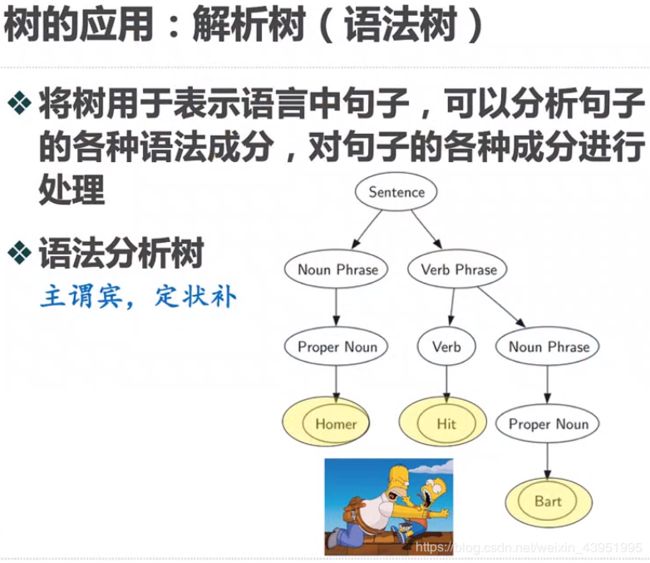
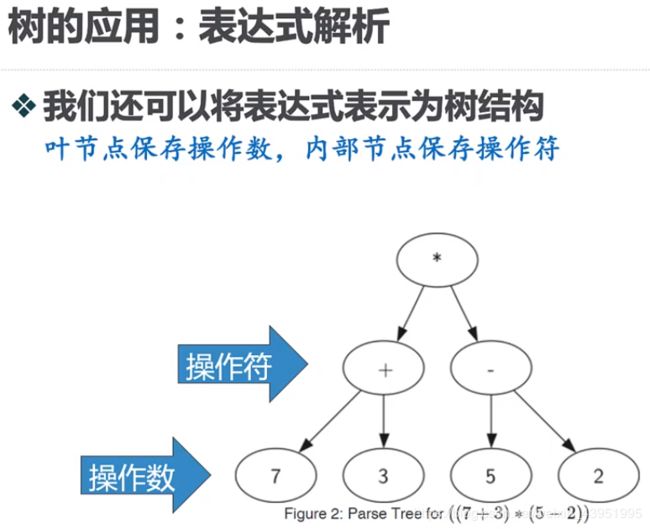
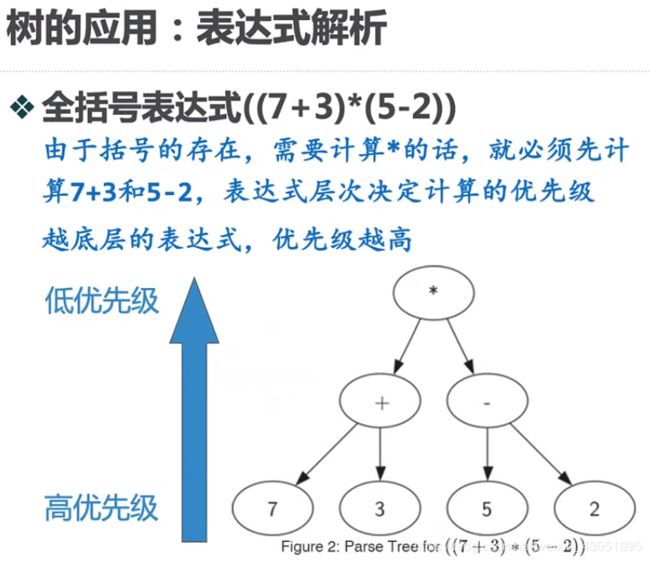
五、树的应用:表达式解析
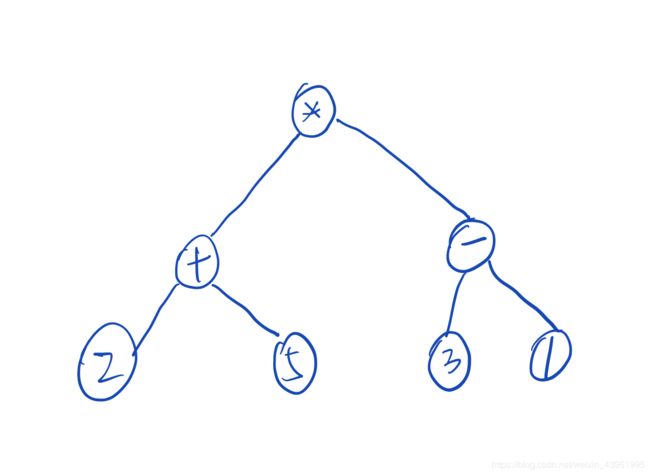
1.表达式解析
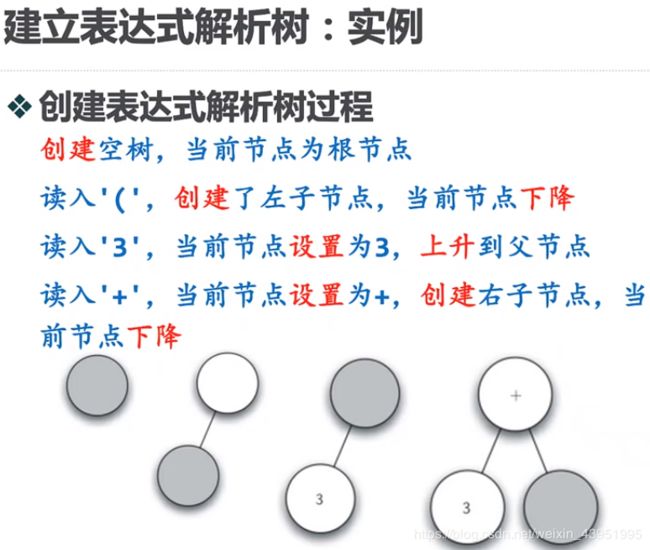
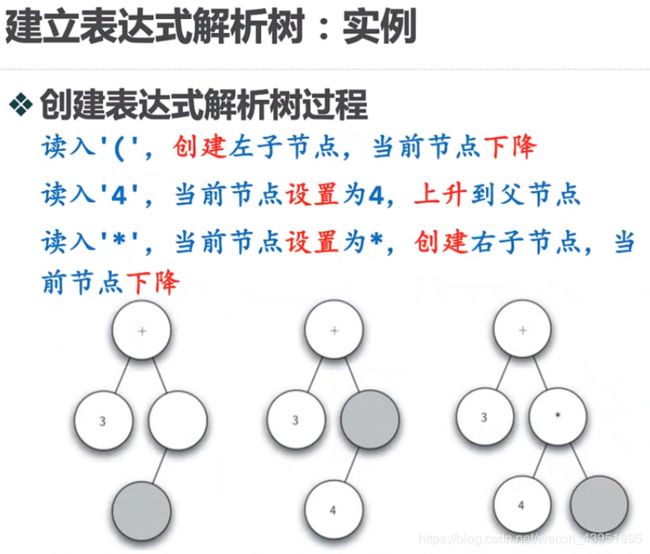
2.建立表达式解析树
def buildPraseTree(fpExp):
fpList=fpExp.split()
pStack=Stack()
eTree=BinaryTree('')
pStack.push(eTree)
currentTree=eTree
for i in fpList:
if i =='(':
currentTree.insertLeft('')
pStack.push(currentTree)
currentTree=currentTree.getLeftChild()
elif i not in ['+','-','*','/',')']:
currentTree.setRootVal(int(i))
parent=pStack.pop()
currentTree=parent
elif i in ['+','-','*','/']:
currentTree.setRootVal(i)
currentTree.insertRight('')
pStack.push(currentTree)
currentTree=currentTree.getRightChild()
elif i ==')':
currentTree=pStack.pop()
else:
raise ValueError
return eTree
![]()
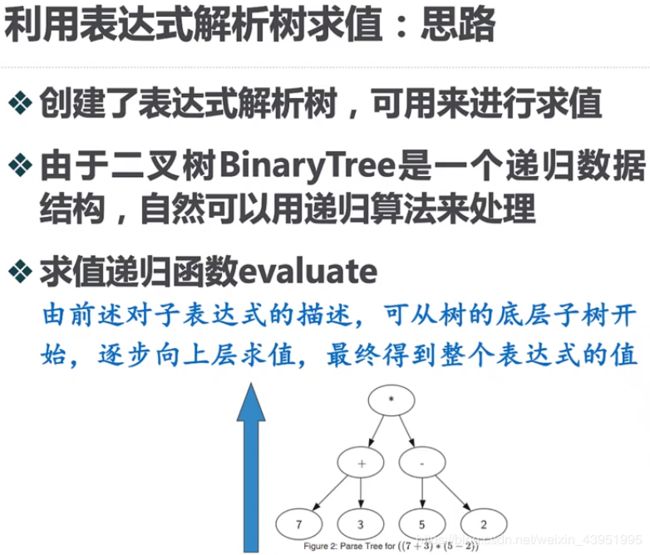
3.利用表达式解析树求值
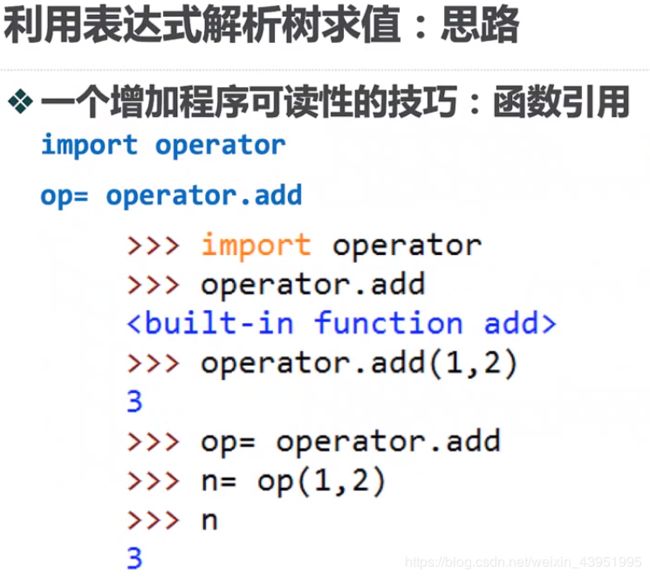
import operator
def evaluate(parseTree):
opers={'+':operator.add,'-':operator.sub,'*':operator.mul,'/':operator.truediv}
leftChildTree=parseTree.getLeftChild()
rightChildTree=parseTree.getRightChild()
if leftChildTree and rightChildTree:
fn=opers[parseTree.getRootVal()]
return fn(evaluate(leftChildTree),evaluate(rightChildTree))
else:
return parseTree.getRootVal()
tree=buildPraseTree('( ( 2 + 5 ) * ( 3 - 1 ) )')
val=evaluate(tree)
print(val)
六、树的遍历
1.树的遍历
2.遍历程序
(1)前序遍历
def preOrder(tree):
if tree!=None:
print(tree.getRootVal())
preOrder(tree.getLeftChild())
preOrder(tree.getRightChild())
(2)中序遍历
def inOrder(tree):
if tree!=None:
inOrder(tree.getLeftChild())
print(tree.getRootVal())
inOrder(tree.getRightChild())
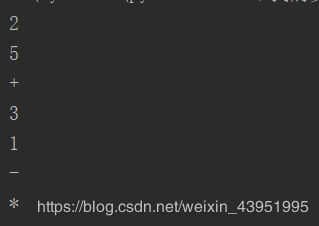
(3)后序遍历
def postOrder(tree):
if tree!=None:
postOrder(tree.getLeftChild())
postOrder(tree.getRightChild())
print(tree.getRootVal())
4.遍历示例
def buildPraseTree(fpExp):
fpList=fpExp.split()
pStack=Stack()
eTree=BinaryTree('')
pStack.push(eTree)
currentTree=eTree
for i in fpList:
if i =='(':
currentTree.insertLeft('')
pStack.push(currentTree)
currentTree=currentTree.getLeftChild()
elif i not in ['+','-','*','/',')']:
currentTree.setRootVal(int(i))
parent=pStack.pop()
currentTree=parent
elif i in ['+','-','*','/']:
currentTree.setRootVal(i)
currentTree.insertRight('')
pStack.push(currentTree)
currentTree=currentTree.getRightChild()
elif i ==')':
currentTree=pStack.pop()
else:
raise ValueError
return eTree
def preOrder(tree):
if tree!=None:
print(tree.getRootVal())
preOrder(tree.getLeftChild())
preOrder(tree.getRightChild())
def inOrder(tree):
if tree!=None:
inOrder(tree.getLeftChild())
print(tree.getRootVal())
inOrder(tree.getRightChild())
def postOrder(tree):
if tree!=None:
postOrder(tree.getLeftChild())
postOrder(tree.getRightChild())
print(tree.getRootVal())
tree=buildPraseTree('( ( 2 + 5 ) * ( 3 - 1 ) )')
preOrder(tree)
inOrder(tree)
postOrder(tree)
def printexp(tree):
sVal=''
if tree:
sVal='('+printexp(tree.getLeftChild())
sVal=sVal+str(tree.getRootVal())
sVal=sVal+printexp(tree.getRightChild())+')'
return sVal
七、优先队列和二叉堆
二叉堆实现优先队列。
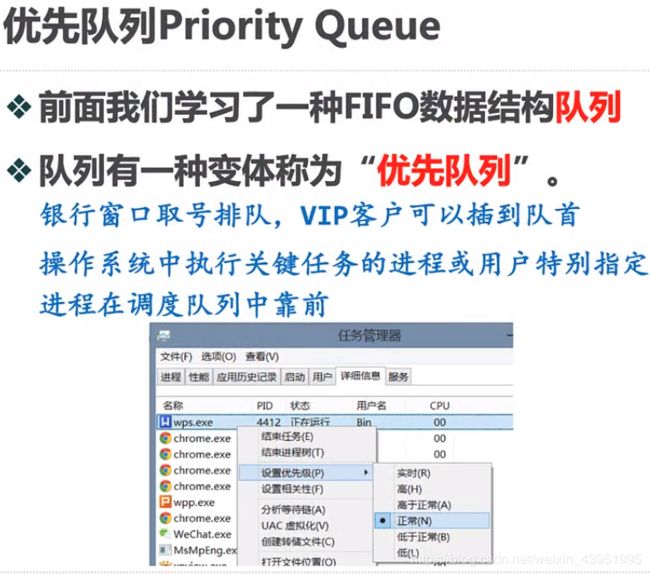
1.优先队列
2.二叉堆实现优先队列
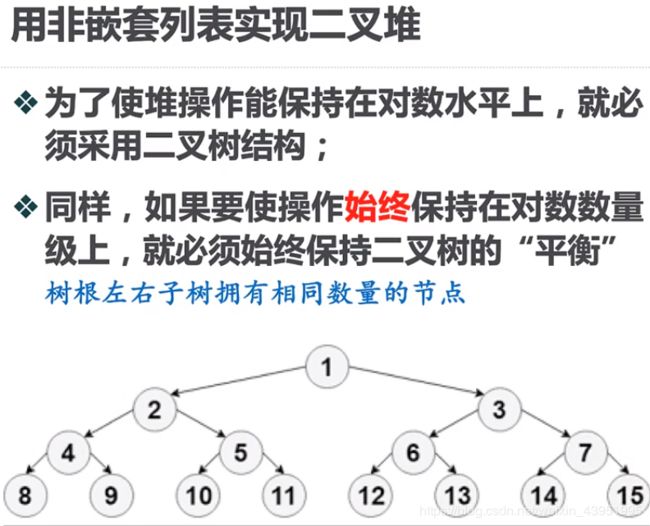
3.用非嵌套列表实现二叉堆
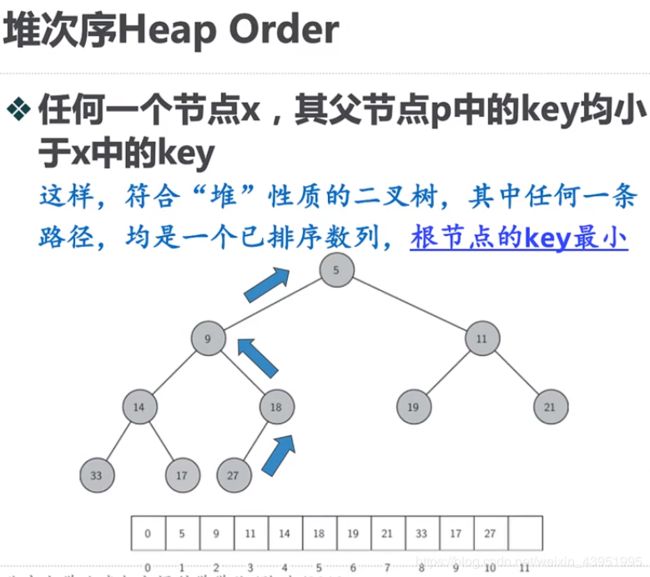
4.堆次序
3.二叉堆的python实现
(1)初始化

(2)insert(key)方法
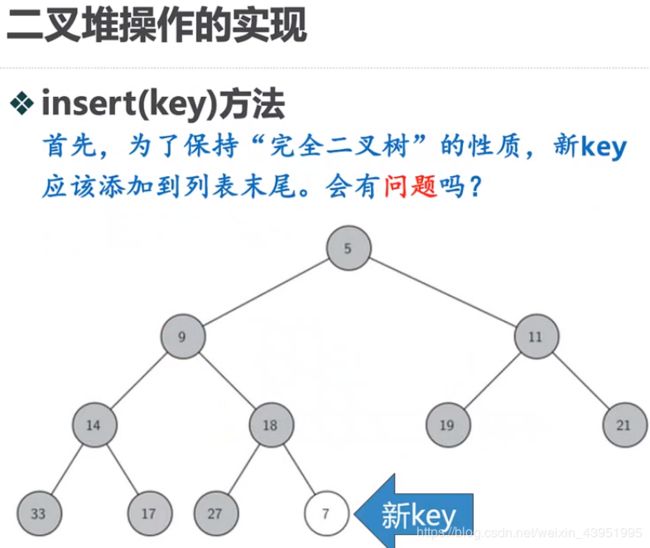
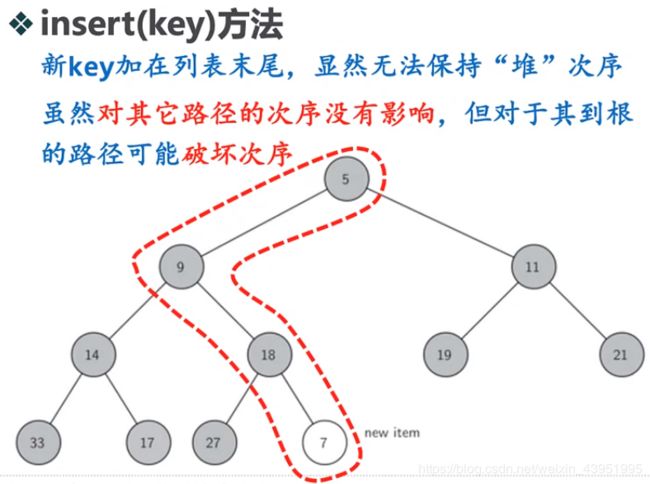


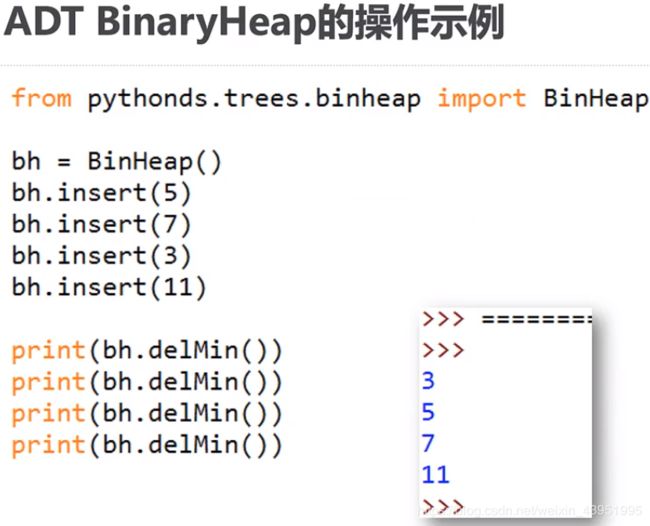
(3)delMin()方法
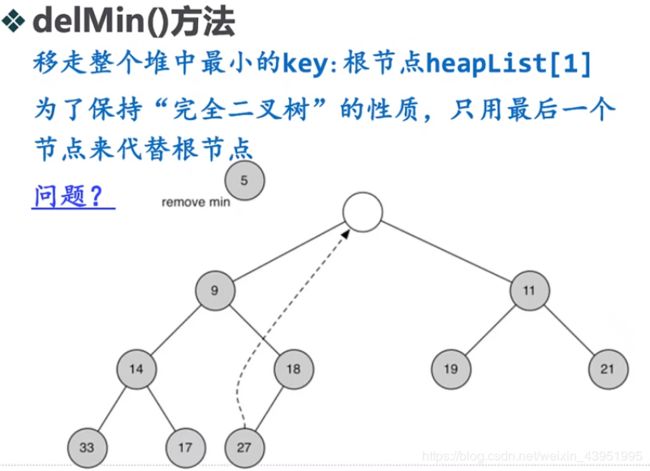

下沉路径的选择:选择较小的子节点交换下沉,

(4)buildHeap(lst)方法
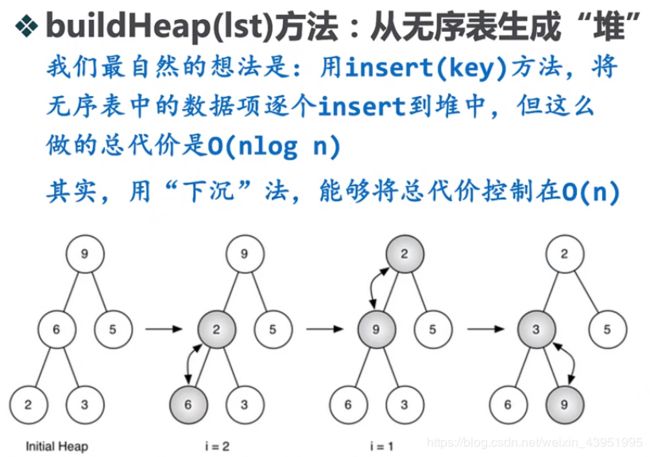

二叉堆操作程序:
class BinHeap:
def __init__(self):
self.heapList=[0]
self.currentSize=0
def insert(self,k):
self.heapList.append(k)
self.currentSize=self.currentSize+1
self.perUp(self.currentSize)
def perUp(self,i):
while i//2>0:
if self.heapList[i]<self.heapList[i//2]:
temp=self.heapList[i//2]
self.heapList[i//2]=self.heapList[i]
self.heapList[i]=temp
i=i//2
def delMin(self):
retval=self.heapList[1]
self.heapList[1]=self.heapList[self.currentSize]
self.currentSize=self.currentSize-1
self.heapList.pop()
self.percDown(1)
return retval
def percDown(self,i):
while (i*2)<=self.currentSize:
mc=self.minChild(i)
if self.heapList[i]>self.heapList[mc]:
temp=self.heapList[i]
self.heapList[i]=self.heapList[mc]
self.heapList[mc]=temp
i=mc
def minChild(self,i):
if i*2+1>self.currentSize:
return i*2
else:
if self.heapList[i*2]<self.heapList[i*2+1]:
return i*2
else:
return i*2+1
def buildHeap(self,alist):
i=len(alist)//2
self.currentSize=len(alist)
self.heapList=[0]+alist[:]
print(len(self.heapList),i)
while i>0:
print(self.heapList,i)
self.percDown(i)
i=i-1
print(self.heapList,i)
八、二叉查找树及操作
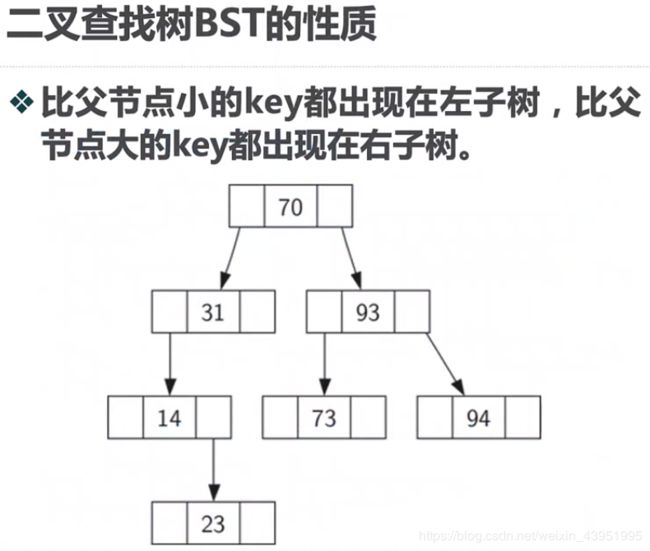
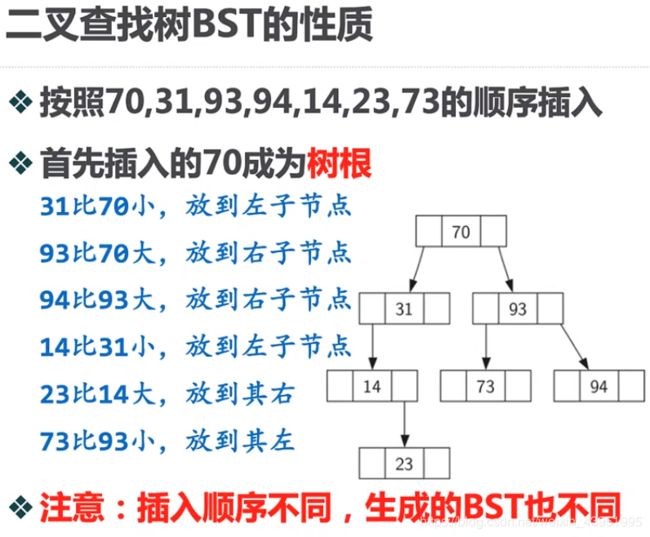
1.二叉查找树
2.二叉查找树的实现
class BinarySearchTree:
def __init__(self):
self.root=None
self.size=0
def length(self):
return self.size
def __len__(self):
return self.size
def __iter__(self):
return self.root.__iter__()
def put(self,key,val):
if self.root:
self._put(key,val,self.root)
else:
self.root=TreeNode(key,val)
self.size=self.size+1
def _put(self,key,val,currentNode):
if key<currentNode.key:
if currentNode.hasLeftChild():
self._put(key,val,currentNode.leftChild)
else:
currentNode.leftChild=TreeNode(key,val,parent=currentNode)
else:
if currentNode.hasRightChild():
self._put(key,val,currentNode.rightChild)
else:
currentNode.rightChild=TreeNode(key,val,parent=currentNode)
def __setitem__(self, key, value):
self.put(key,value)
def get(self,key):
if self.root:
res=self.__get(key,self.root)
if res:
return res.payload
else:
return None
else:
return None
def _get(self,key,currentNode):
if not currentNode:
return None
elif currentNode.key==key:
return currentNode
elif key<currentNode.key:
return self._get(key,currentNode.leftChild)
else:
return self._get(key,currentNode.rightChild)
def __getitem__(self, key):
return self.get(key)
def __contains__(self, key):
if self._get(key,self.root):
return True
else:
return False
def __delitem__(self, key):
self.delete(key)
def delete(self,key):
if self.size>1:
nodeToRemove=self._get(key,self.root)
if nodeToRemove:
self.remove(nodeToRemove)
self.size=self.size-1
else:
raise KeyError('Error,key not in tree')
elif self.size==1 and self.root.key==key:
self.root=None
self.size=self.size-1
else:
raise KeyError('Error,key not in tree')
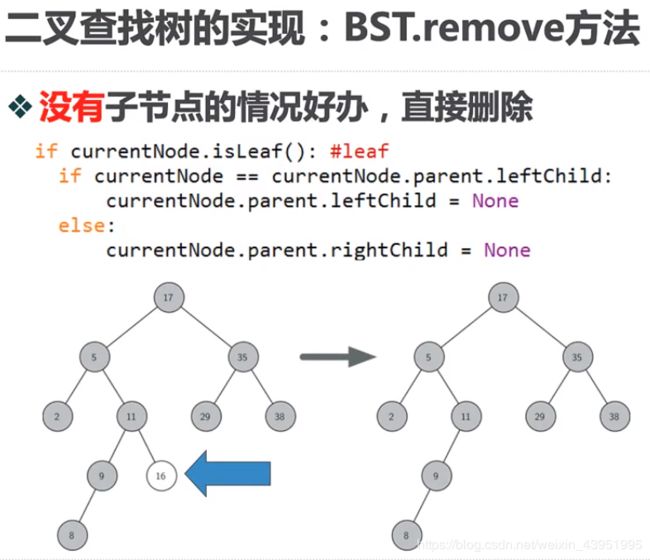
def remove(self,currentNode):
if currentNode.isLeaf(): #leaf
if currentNode == currentNode.parent.leftChild:
currentNode.parent.leftChild = None
else:
currentNode.parent.rightChild = None
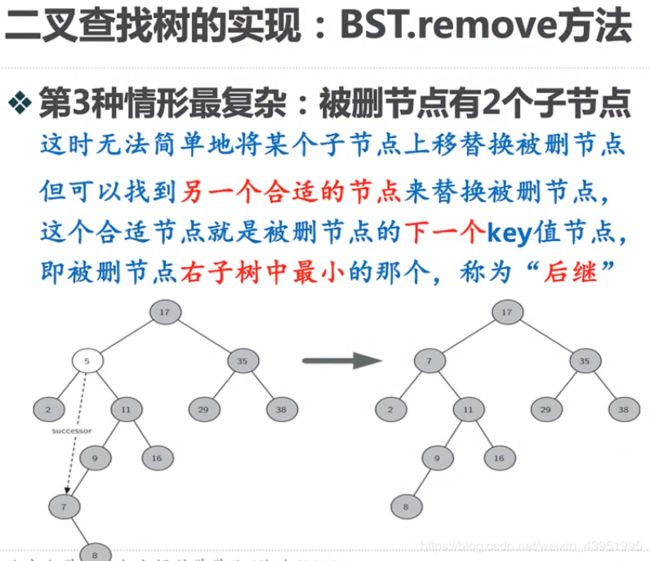
elif currentNode.hasBothChildren(): #interior
succ = currentNode.findSuccessor()
succ.spliceOut()
currentNode.key = succ.key
currentNode.payload = succ.payload
else: # this node has one child
if currentNode.hasLeftChild():
if currentNode.isLeftChild():
currentNode.leftChild.parent = currentNode.parent
currentNode.parent.leftChild = currentNode.leftChild
elif currentNode.isRightChild():
currentNode.leftChild.parent = currentNode.parent
currentNode.parent.rightChild = currentNode.leftChild
else:
currentNode.replaceNodeData(currentNode.leftChild.key,
currentNode.leftChild.payload,
currentNode.leftChild.leftChild,
currentNode.leftChild.rightChild)
else:
if currentNode.isLeftChild():
currentNode.rightChild.parent = currentNode.parent
currentNode.parent.leftChild = currentNode.rightChild
elif currentNode.isRightChild():
currentNode.rightChild.parent = currentNode.parent
currentNode.parent.rightChild = currentNode.rightChild
else:
currentNode.replaceNodeData(currentNode.rightChild.key,
currentNode.rightChild.payload,
currentNode.rightChild.leftChild,
currentNode.rightChild.rightChild)
class TreeNode:
def __init__(self,key,val,left=None,right=None,parent=None):
self.key=key
self.payload=val
self.leftChild=left
self.rightChild=right
self.parent=parent
def hasLeftChild(self):
return self.leftChild
def hasRightChild(self):
return self.rightChild
def isLeftChild(self):
return self.parent and self.parent.leftChild==self
def isRightChild(self):
return self.parent and self.parent.rightChild==self
def isRoot(self):
return not self.parent
def isLeaf(self):
return not (self.rightChild or self.leftChild)
def hasAnyChild(self):
return self.leftChild or self.rightChild
def hasBothChild(self):
return self.rightChild and self.leftChild
def replaceNodeData(self,key,value,lc,rc):
self.key=key
self.payload=value
self.leftChild=lc
self.rightChild=rc
if self.hasLeftChild():
self.leftChild.parent=self
if self.hasRightChild():
self.rightChild.parent=self
def __iter__(self):
if self:
if self.hasLeftChild():
for elem in self.leftChild:
yield elem
yield self.key
if self.hasRightChild():
for elem in self.rightChild:
yield elem
def findSuccessor(self):
succ = None
if self.hasRightChild():
succ = self.rightChild.findMin()
else:
if self.parent:
if self.isLeftChild():
succ = self.parent
else:
self.parent.rightChild = None
succ = self.parent.findSuccessor()
self.parent.rightChild = self
return succ
def spliceOut(self):
if self.isLeaf():
if self.isLeftChild():
self.parent.leftChild = None
else:
self.parent.rightChild = None
elif self.hasAnyChildren():
if self.hasLeftChild():
if self.isLeftChild():
self.parent.leftChild = self.leftChild
else:
self.parent.rightChild = self.leftChild
self.leftChild.parent = self.parent
else:
if self.isLeftChild():
self.parent.leftChild = self.rightChild
else:
self.parent.rightChild = self.rightChild
self.rightChild.parent = self.parent
def findMin(self):
current = self
while current.hasLeftChild():
current = current.leftChild
return current
九、AVL树
十、小结
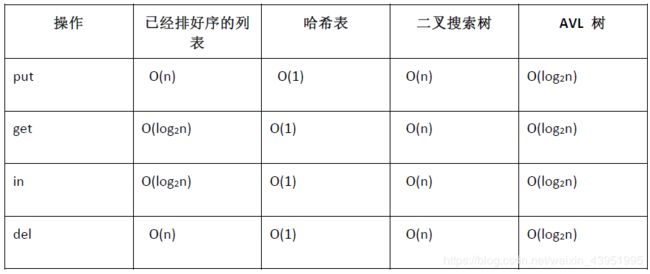
通过过去两章,我们已经看过了好几种可以用于实现 Map 抽象数据类型的数据结构。列表的二分搜索,哈希表,二叉搜索树和平衡二叉树。作为这一章的结束,让我们总结这些数据结构在 Map 的对键值 key 的操作中的性能。