模型评估（二）—— ROC, AUC, 和ROC曲线绘制过程

ROC的全称是Receiver Operating Characteristic，也是模型评估中的重要概念之一。本文将结合 sklearn.metrics.roc_curve官方文档的例子来说明ROC曲线的绘制过程, 以及AUC的计算。

1) TPR和FPR

在前一篇文章里模型评估（一）—— 准确率(Accuracy)，精确率(Precision)，召回率（Recall），F1-Score的总结介绍过TP,TN,FP,FN和Recall，Precision的概念， 而本文要用到的指标是真阳性率：True Postive Rate（TPR）和假阳性率：False Postive Rate（FPR），计算公式分别为：
$TPR=\frac{TP}{TP+FN},FPR=\frac{FP}{TN+FP}$.

2）官方文档的例子

这里用一个sklearn里的metrics.roc_curve官方文档里的例子：sklearn.metrics.roc_curve

import numpy as np
from sklearn import metrics
y=np.array([1,1,2,2])
scores=np.array([0.1,0.4,0.35,0.8])
fpr,tpr,thresholds=metrics.roc_curve(y,scores,pos_label=2)

输出结果为：

fpr
array([0. , 0. , 0.5, 0.5, 1. ])
tpr
array([0. , 0.5, 0.5, 1. , 1. ])
thresholds
array([1.8 , 0.8 , 0.4 , 0.35, 0.1 ])

ROC曲线就是（fpr,tpr）坐标连接起来：

3）ROC Curve绘制过程

计算ROC曲线之前，需要给出一组True label(例子里的y）和对应的概率（例子里的scores）：预测时，每个label为正例的概率。pos_label=2是当label不是0和1（比如是例子中的1和2时），指定2为正例。metrics.roc_curve会输出三组值：fpr, tpr和thresholds。其中threholds其实就是将这一组概率从大到小排列，计算时:

1）先把所有样本都预测为反例，这时候TPR和FPR都是0，也就是为什么例子中fpr和tpr的输出中第一个值都是0。

2）从最大的那个概率开始，每一个概率被依次设置为分类阈值thresholds：当score>=threshold时，预测为正例。

3） 遍历每一个阈值，得到每一个阈值下的TPR和FPR，一共四组，分别是ROC曲线的纵轴和横轴，然后连起来就组成了ROC曲线（以上例子中thresholds的第一个值是1.8, 按照官方文档，因为在最开始的（0，0）并没有在预测，第一个值就设定为max（score）+1）。

如果值多一点的话可能就长这样(我在Python中随机generate了100个0和1作为y，和100个uniformly distributed的0到1之间的值作为score)：

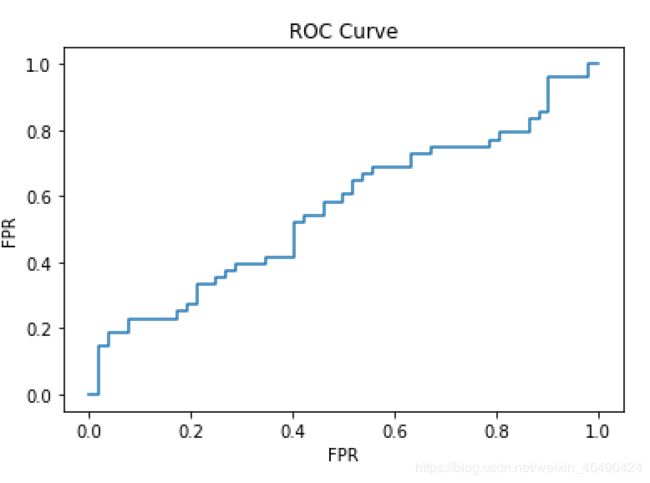
4）AUC的计算

当我们要比较模型时，可以选择比较ROC曲线下面的面积：Area Under Curve,或AUC，我们希望选择AUC较大的那个模型。一般来说，AUC的值在0.5到1之间。如果小于0.5，说明还不如瞎猜。如果要估算AUC的值，可以考虑将ROC曲线下面的面积切割为数个梯形的面积然后相加。或者考虑，当随机取一对正负例样本，正例的score大于负例的score的概率是多少？这个值就是AUC。所以也可以这样算：把n个正例和m个负例两两组合，得到$m\times n$组，算出有多少组正例的score大于负例的score。

参考文档:
https://scikit-learn.org/stable/modules/generated/sklearn.metrics.roc_curve.html