概念回顾
Fst:群体间遗传分化指数,是种群分化和遗传距离的一种衡量方法,分化指数越大,差异越大。适用于亚群体间多样性的比较。
用于衡量种群分化程度,取值从0到1,为0则认为两个种群间是随机交配的,基因型完全相似;为1则表示是完全隔离的,完全不相似。它往往从基因的多样性来估计,比如SNP或者microsatellites(串联重复序列一种,长度小于等于10bp)。是一种以哈温平衡为前提的种群遗传学统计方法。
两个种群之间遗传差异的基本测量是统计量FST。在遗传学中,F一词通常代表“近亲繁殖”,它倾向于减少群体中的遗传变异。遗传变异可以用杂合度来衡量,所以F一般表示群体中杂合性的减少。 FST是与它们所属的总群体相比,亚群体中杂合性的减少量。
具体可以下面的公式表示:
Fst= (Ht-Hs)/ Ht
Hs:亚群体中的平均杂合度
Ht:复合群体中的平均杂合度
理论上计算Fst的步骤
理论上要估算FST,需要以下步骤:
- 找出每个亚群的等位基因频率。
- 查找复合群体的平均等位基因频率
- 计算每个亚群的杂合度(2pq)
- 计算这些亚群杂合度的平均值,这是HS。
- 根据总体等位基因频率计算杂合度,这是HT。
- 最后,计算FST =(HT-HS)/ HT
具体例子
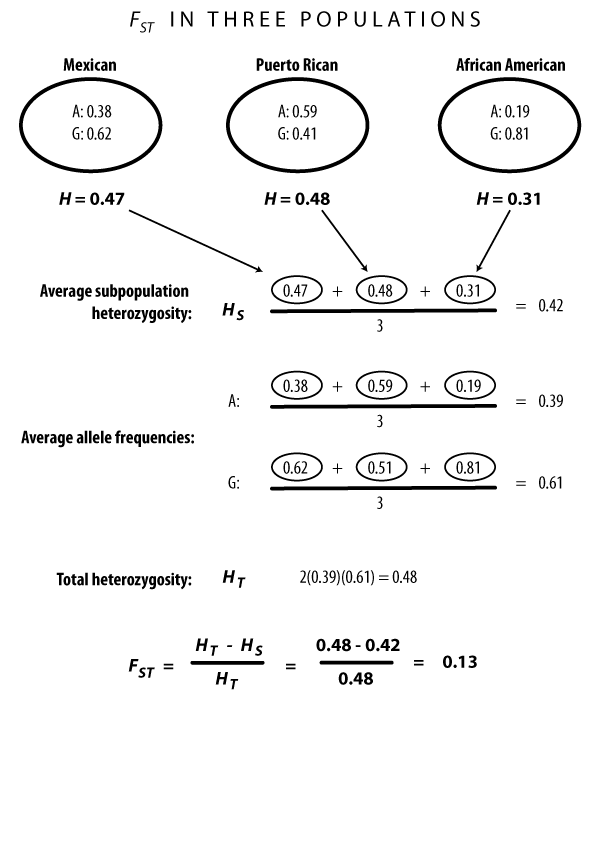
基因SLC24A5是黑色素表达途径的关键部分,其导致皮肤和毛发色素沉着。与欧洲较轻的皮肤色素密切相关的SNP是rs1426654。 SNP有两个等位基因A和G,其中G与轻度皮肤相关,在犹他州的欧裔美国人中,频率为100%。美洲印第安人与美国印第安人混血儿的SNP在频率上有所不同。墨西哥的样本有38%A和62%G;在波多黎各,频率分别为59%A和41%G,查尔斯顿的非裔美国人样本中有19%A和81%G.这个例子中的FST是什么?
手工计算的步骤如下:
在得到每个群体中等位基因的频率后:
首先第一步是计算每个亚群的杂合度H,这一步简单H=2pq (p和q是对应群体中等位基因的频率)
第二步计算这些亚群杂合度的平均值HS,取三个不同种群中的H值,除去平均数3,得到结果
第三步,计算群体等位基因频率,和上述方法类似,取每个等位基因在对应种群中的频率叠加除去平均数。
第四步,计算所有群体中的杂合度HT,使用2pq,p和q是群体中的等位基因频率,在第三步骤已经算好了。
最后,根据计算公式算出Fst。
在实际中,当然不可能用手工对每个位点进行这样的计算,怎样在电脑中分析FST等值,会在下次内容中介绍。
实战
当然了,实际中我们并不需要像上述例子那样逐个计算。等位基因频率的信息都藏在snp calling后的vcf中,再使用恰当的工具就可以快速计算出Fst。下面给大家介绍一种比较popular的计算Fst的方法(还有其他方法不限于一种),使用vcftools:
##对每一个SNP变异位点进行计算
vcftools --vcf test.vcf --weir-fst-pop 1_population.txt --weir-fst-pop 2_population.txt --out p_1_2—single
##按照区域来计算
vcftools --vcf test.vcf --weir-fst-pop 1_population.txt --weir-fst-pop 2_population.txt --out p_1_2_bin --fst-window-size 500000 --fst-window-step 50000
# test.vcf是SNP calling 过滤后生成的vcf 文件;
# p_1_2_3 生成结果的prefix
# 1_population.txt是一个文件包含同一个群体中所有个体,一般每行一个个体。个体名字要和vcf的名字对应。
# 2_population.txt 包含了群体二中所有个体。
#计算的窗口是500kb,而步长是50kb (根据你的需其可以作出调整)。我们也可以只计算每个点的Fst,去掉参数(--fst-window-size 500000 --fst-window-step 50000)即可。
分别对不同结果进行图形绘制
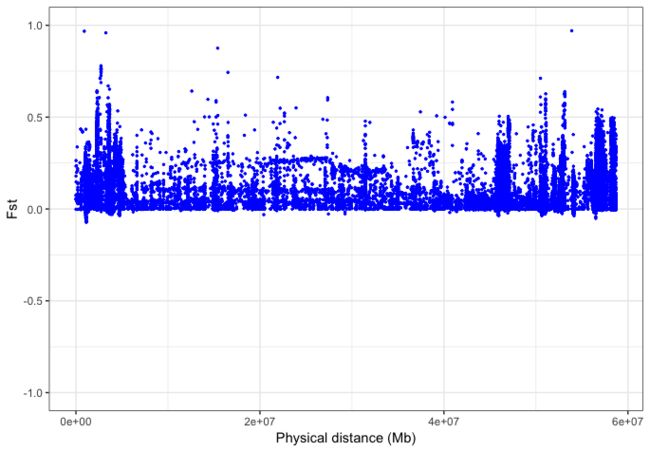
##图1
library(ggplot2)
data<-read.table("test1.out.windowed.weir.fst",header=T)
sc3 = subset(data,CHROM=="Gm01")
p <- ggplot(sc3,aes(x=BIN_END/1000000,y=WEIGHTED_FST)) + geom_point(size=0.5, colour="blue") + xlab("Physical distance (Mb)")+ ylab("Fst") + ylim(-1,1)
p + theme_bw()
##图2
library(ggplot2)
data<-read.table("test.out.weir.fst",header=T)
sc3 = subset(data,CHROM=="Gm01")
p <- ggplot(sc3,aes(x=POS,y=WEIR_AND_COCKERHAM_FST)) + geom_point(size=0.5, colour="blue") + xlab("Physical distance (Mb)")+ ylab("Fst") + ylim(-1,1)
p + theme_bw()
可以看到两幅图还是基本对应的,然后对一些接近1,与大部分点偏离比较高的点可以将其与功能注释相结合,还有一些选择压力分析的工具相结合,寻找出其对应的基因,观察该基因是否是被选择。Pi也是选择分析中一个很要的参数,这一部分内容有时间这一点以后再补回来。
参考文章:
https://blog.csdn.net/u014182497/article/details/52672308
http://www.omicshare.com/forum/thread-3688-1-1.html