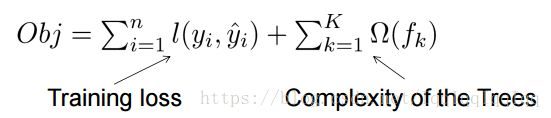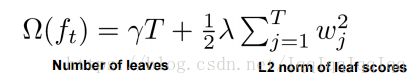机器学习中常见的问题整理（一）

本文整理了一些常见的机器学习中可能会遇到的问题，这些问题包括基本概念的理解，各种场景下模型的选择等问题，以及一些常见概念背后的原因，结果和改进思路等。

1.对于xgboost，还有必要做很多特征工程吗？

特征工程是个很广的概念，包括特征筛选、特征变换、特征合成、特征提取等等。

对于xgboost，它能够很好地做到特征选择，所以这一点不用我们去操心太多。

至于特征变换（离散化、归一化、标准化、取log等等），我们也不需要做太多，因为xgboost是基于决策树，决策树自然能够解决这些。相比较来说，线性模型则需要做离散化或者取log处理。因为xgboost（树类模型）不依赖于线性假设。但是对于分类特征，xgboost需要对其进行独热编码，否则无法训练模型。

xgboost也可以免于一部分特征合成的工作，比如线性回归中的交互项a:b，在树类模型中都可以自动完成。但是对于加法a+b，减法a-b，除法a-b这类合成的特征，则需要手动完成。

绝大部分模型都无法自动完成的一步就是特征提取。很多nlp的问题或者图象的问题，没有现成的特征，你需要自己去提取这些特征，这些是我们需要人工完成的。

综上来说，xgboost的确比线性模型要省去很多特征工程的步骤。但是特征工程依然是非常必要的。

2.什么时候该用LASSO，什么时候该用Ridge？

这两个都是正则化的手段。LASSO是基于回归系数的一范数，Ridge是基于回归系数的二范数的平方。根据Hastie, Tibshirani, Friedman的经典教材，如果你的模型中有很多变量对模型都有些许影响，那么用Ridge；如果你的模型中只有少量变量对模型很大影响，那么用LASSO。

LASSO可以使得很多变量的系数为0（相当于降维），但是Ridge却不能。

因为Ridge计算起来更快，所以当数据量特别大的时候，更倾向于用Ridge。

最万能的方法是用LASSO和Ridge都试一试，比较两者Cross Validation的结果。

如果有很多多重共线性的变量，ridge的效果比lasso好。

最后补充一下，你也可以尝试一下两者的混合-Elastic Net。

3.如何简单理解正则化？

从模型复杂度来理解的话，正则化就是奥卡姆剃刀正则化是奥卡姆剃刀的具体实现，在保持预测能力相当时，降低模型复杂度。

4.L2-norm为什么会让模型变得更加简单？

斯坦福的一个讲义里说，在特征都被标准化处理的情况下，回归系数越大，模型的复杂度越大。所以特征系数变成0，模型复杂度会下降；系数变小，当然也是复杂度下降。

5.两个变量不相关但是也不独立的例子？

假设X是个随机变量服从标准正态分布，另一个随机变量Y满足Y=X2，那么它们的协方差

cov(X,Y)=E(XY)−E(X)E(Y)=E(X3)−E(X)E(X2)=0−0×E(X2)=0

协方差为0，说明X和Y不相关。但是显然X和Y不独立。

6.xgboost是怎么做到regularization的？xgboost的目标函数是损失函数+惩罚项。从下面的式子可以看出，树越复杂，惩罚越重。

树的复杂度定义如下：

叶节点的数量和叶节点的得分越高，树就越复杂。

7.为什么lightgbm比xgb快？

LightGBM采用了基于梯度的单边采样（GOSS）的方法。

在过滤数据样例寻找分割值时，LightGBM 使用的是全新的技术：基于梯度的单边采样（GOSS）；而 XGBoost 则通过预分类算法和直方图算法来确定最优分割。在 Adaboost 中，样本权重是展示样本重要性的很好的指标。但在梯度提升决策树（GBDT）中，并没有天然的样本权重，因此 Adaboost 所使用的采样方法在这里就不能直接使用了，这时我们就需要基于梯度的采样方法。

梯度表征损失函数切线的倾斜程度，所以自然推理到，如果在某些意义上数据点的梯度非常大，那么这些样本对于求解最优分割点而言就非常重要，因为算其损失更高。

GOSS 保留所有的大梯度样例，并在小梯度样例上采取随机抽样。比如，假如有 50 万行数据，其中 1 万行数据的梯度较大，那么我的算法就会选择（这 1 万行梯度很大的数据+x% 从剩余 49 万行中随机抽取的结果）。如果 x 取 10%，那么最后选取的结果就是通过确定分割值得到的，从 50 万行中抽取的 5.9 万行。在这里有一个基本假设：如果训练集中的训练样例梯度很小，那么算法在这个训练集上的训练误差就会很小，因为训练已经完成了。为了使用相同的数据分布，在计算信息增益时，GOSS 在小梯度数据样例上引入一个常数因子。因此，GOSS 在减少数据样例数量与保持已学习决策树的准确度之间取得了很好的平衡。上文部分转载机器之心。原论文链接如下

https://papers.nips.cc/paper/6907-lightgbm-a-highly-efficient-gradient-boosting-decision-tree.pdf

8.xgboost怎么调参？

以python里XGBClassifier为例。首先，要确定哪些参数要调，以下是比较重要和常用的参数。

max_depth: 每棵树的最大深度。太小会欠拟合，太大过拟合。正常值是3到10。

learning_rate: 学习率，也就是梯度下降法中的步长。太小的话，训练速度太慢，而且容易陷入局部最优点。通常是0.0001到0.1之间。

n_estimators: 树的个数。并非越多越好，通常是50到1000之间。

colsample_bytree: 训练每个树时用的特征的数量。1表示使用全部特征，0.5表示使用一半的特征。

subsample: 训练每个树时用的样本的数量。与上述类似，1表示使用全部样本，0.5表示使用一半的样本。

reg_alpha: L1正则化的权重。用来防止过拟合。一般是0到1之间。

reg_lambda: L2正则化的权重。用来防止过拟合。一般是0到1之间。

min_child_weight: 每个子节点所需要的样本的数量（加权的数量）。若把它设置为大于1的数值，可以起到剪枝的效果，防止过拟合。

以上只是作为参考，通常我们只对其中的少数几个进行调参，模型就可以达到很好的效果。

下一步就是对这些参数进行优化，最常用的是Grid Search。比如说我们要优化max_depth 和learning_rate。max_depth的候选取值为[3, 4, 5, 6, 7]，learning_rate候选取值为[0.0001, 0.001, 0.01, 0.1]。那么我们就需要尝试这两个参数所有的可能的组合（共5*4=20个不同的组合）。通过交叉验证，我们可以得到每个组合的预测评价结果，最后从这20个组合中选择最优的组合。

Grid Search的想法简单易行，但是缺陷就是当我们需要对很多参量进行优化时，我们需要遍历太多的组合，非常耗时。比如说我们有5个参量需要优化，每个参量又有5个候选值，那么就一共有5*5*5*5*5=3125种不同的组合需要尝试，非常耗时。

另外一个常用的方法Random Search就可以解决这个问题。Random Search是从所有的组合中随机选出k种组合，进行交叉验证，比较它们的表现，从中选出最佳的。虽然Random Search的结果不如Grid Search，但是Random Search通常以很小的代价获得了与Grid Search相媲美的优化结果。所以实际调参中，特别是高维调参中，Random Search更为实用。

值得注意的是，本文仅代表部分同学的观点，如有更多想法欢迎交流与探讨。
扫描下面二维码关注本公众号可以查看后续更新~