线性回归(二)—— 多元线性回归
多元线性回归
目的
当影响结果的原因不止一个的时候,就不能用一元线性回归了。比如说二元线性回归就是得用一个平面拟合。这时候我们的目的也就不只是找出最好的 θ 0 \theta_0 θ0和 θ 1 \theta_1 θ1,而是要找出好多 θ \theta θ.
h ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 + … θ n x n h(x) = \theta_0+\theta_1x_1+\theta_2x_2+…\theta_nx_n h(x)=θ0+θ1x1+θ2x2+…θnxn
代价函数
J ( θ 0 , θ 1 , … , θ n ) = 1 2 m ∑ i = 1 m ( y i − h θ ( x i ) ) 2 J(\theta_0,\theta_1,…,\theta_n) = \frac{1}{2m}\sum_{i=1}^{m}{(y^i-h_\theta(x^i))^2} J(θ0,θ1,…,θn)=2m1i=1∑m(yi−hθ(xi))2
代价函数还是这个东西…
梯度下降
θ j : = θ j − α ∂ ∂ θ j J ( θ 0 , θ 1 , … , θ n ) \theta_j := \theta_j - \alpha\frac{∂}{∂\theta_j}J(\theta_0,\theta_1,…,\theta_n) θj:=θj−α∂θj∂J(θ0,θ1,…,θn)
梯度下降的迭代函数也还是这个…
求一下偏导之后也就是:
θ j : = θ j − α 1 n ∑ i = 1 n ( h θ ( x ) − y ) x j \theta_j := \theta_j - \alpha\frac{1}{n}\sum_{i=1}^{n}(h_\theta(x)-y)x_j θj:=θj−αn1i=1∑n(hθ(x)−y)xj
x 0 x_0 x0是1,因为要保证 θ 0 \theta_0 θ0的系数是1.
梯度下降实现二元线性回归
# encoding:utf-8
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# 读入数据
data = np.genfromtxt("../data/Delivery.csv", delimiter=',')
# 切分数据
x_data = data[:, :-1] # -1代表最后一列,x中存了除最后一列外的所有数据
y_data = data[:, -1]
# 学习率learning rate
lr = 0.0001
# 参数
a = 0
b = 0
c = 0
# 迭代次数
epochs = 1000
# 定义代价函数
def compute_loss(a, b, c, x_data, y_data):
total_loss = 0
for i in range(0, len(x_data)):
# 真实值减预测值平方后求和
total_loss += (y_data[i] - (c * x_data[i, 1] + b * x_data[i, 0] + b)) ** 2
return total_loss / 2.0 / float(len(x_data))
# 用梯度下降法求出最好的参数
def gradient_descent_runner(x_data, y_data, a, b, c, lr, epochs):
# 总数据量m
m = float(len(x_data))
# 开始迭代计算
for i in range(epochs):
# 这两个临时变量用来存当前的“梯度”
a_grad = 0
b_grad = 0
c_grad = 0
# 计算“梯度”
for j in range(0, len(x_data)):
a_grad += (1 / m) * ((c * x_data[j, 1] + b * x_data[j, 0] + a) - y_data[j])
b_grad += (1 / m) * x_data[j, 0] * ((c * x_data[j, 1] + b * x_data[j, 0] + a) - y_data[j])
c_grad += (1 / m) * x_data[j, 1] * ((c * x_data[j, 1] + b * x_data[j, 0] + a) - y_data[j])
# 更新参数
a = a - (lr * a_grad)
b = b - (lr * b_grad)
c = c - (lr * c_grad)
return a, b, c
# 输出相关信息
print("初始 a = {0},b = {1},c = {2} 代价函数的值为 {3}".format(a, b, c, compute_loss(a, b, c, x_data, y_data)))
a, b, c = gradient_descent_runner(x_data, y_data, a, b, c, lr, epochs)
print("现在 a = {0},b = {1},c = {2} 代价函数的值为 {3}".format(a, b, c, compute_loss(a, b, c, x_data, y_data)))
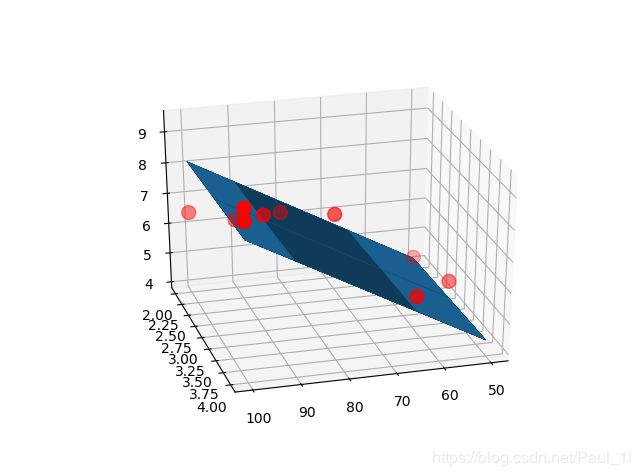
# 画图
ax = plt.figure().add_subplot(111, projection='3d')
ax.scatter(x_data[:, 0], x_data[:, 1], y_data, c='r', marker='o', s=100)
x0 = x_data[:, 0]
x1 = x_data[:, 1]
# 生成网格矩阵
x0, x1 = np.meshgrid(x0, x1)
z = a + b * x0 + c * x1
ax.plot_surface(x0, x1, z)
plt.show()
调用sklearn库实现二元线性回归
# encoding:utf-8
import numpy as np
from sklearn import linear_model
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# 导入数据
data = np.genfromtxt("../data/Delivery.csv", delimiter=',')
# 切分数据
x_data = data[:, :-1]
y_data = data[:, -1]
# 创建并拟合模型
model = linear_model.LinearRegression()
model.fit(x_data, y_data)
# 画图
ax = plt.figure().add_subplot(111, projection='3d')
ax.scatter(x_data[:, 0], x_data[:, 1], y_data, c='brown', marker='o', s=100)
x0 = x_data[:, 0]
x1 = x_data[:, 1]
# 生成网格矩阵
x0, x1 = np.meshgrid(x0, x1)
z = model.intercept_ + model.coef_[0] * x0 + model.coef_[1] * x1
ax.plot_surface(x0, x1, z)
plt.show()