利用MATLAB求解非线性优化问题---fgoalattain函数详解及应用案例

最近在做方程组的非线性优化问题，用到了fgoalattain函数，总结一下：

1. 意义
   解决多目标的非线性优化问题
2. 函数形式
   函数表示形式如下：
   
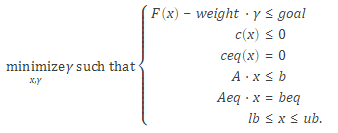
   上式中，weight, goal, b和beq 是向量(组)，A 和Aeq 是矩阵, c(x), ceq(x)和F(x) 返回值为向量的函数，函数可以是非线性的，x, lb, ub 可以以向量或者矩阵的形式传递或者表示;
3. 在不同场景下的语法形式

x = fgoalattain(fun,x0,goal,weight)
x = fgoalattain(fun,x0,goal,weight,A,b)
x = fgoalattain(fun,x0,goal,weight,A,b,Aeq,beq)
x = fgoalattain(fun,x0,goal,weight,A,b,Aeq,beq,lb,ub)
x = fgoalattain(fun,x0,goal,weight,A,b,Aeq,beq,lb,ub,nonlcon) 
x = fgoalattain(fun,x0,goal,weight,A,b,Aeq,beq,lb,ub,nonlcon,options)
x = fgoalattain(problem)
[x,fval] = fgoalattain(...)
[x,fval,attainfactor] = fgoalattain(...) 
[x,fval,attainfactor,exitflag] = fgoalattain(...)
[x,fval,attainfactor,exitflag,output] = fgoalattain(...)
[x,fval,attainfactor,exitflag,output,lambda] = fgoalattain(...)

4. 描述

x = fgoalattain(fun,x0,goal,weight)  的作用是使函数fun提供的目标函数通过改变x的值来实现goal指定的目标，x的数值从x0开始，权重由weight指定；
x = fgoalattain(fun,x0,goal,weight,A,b) 的作用是解决线性不等式A*x ≤ b的目标优化问题；
x = fgoalattain(fun,x0,goal,weight,A,b,Aeq,beq) 的作用是解决线性等式Aeq * x = beq的目标优化问题。 如果不存在不等式，则通过指定设置A = []和b = []的形式进行填充。
x = fgoalattain(fun,x0,goal,weight,A,b,Aeq,beq,lb,ub) 的作用是在以上式子的基础上，在x中的设计变量上定义了一组下限和上限，因此解决方案始终在lb≤x≤ub的范围内。
x = fgoalattain(fun,x0,goal,weight,A,b,Aeq,beq,lb,ub,nonlcon) 的作用是将目标优化问题置于nonlcon参数中定义的非线性不等式c（x）或非线性等式ceq（x）。 fgoalattain优化使得c（x）≤0且ceq（x）= 0.如果不存在边界，则设置lb = []或ub = []；
x = fgoalattain(fun,x0,goal,weight,A,b,Aeq,beq,lb,ub,nonlcon,options)的作用是通过options中指定的优化选项进行最小化优化，选项设置可以使用optimoptions；
x = fgoalattain(problem) 的作用是找到问题(problem)的最小值，其中问题是输入参数中描述的结构;其中我们可以通过从Optimization应用程序导出的问题来创建问题结构；
[x,fval] = fgoalattain(...) 返回在解x的过程中fun计算的目标函数的值；
[x,fval,attainfactor] = fgoalattain(...) 返回解x处的目标达到因子；
[x,fval,attainfactor,exitflag] = fgoalattain(...)返回exitflag参数，描述计算的退出条件；
[x,fval,attainfactor,exitflag,output] = fgoalattain(...)返回包含优化信息的输出参数output；
[x,fval,attainfactor,exitflag,output,lambda] = fgoalattain(...) 返回包含拉格朗日乘子的lambda参数。

5. 函参详解
   <1>. fun：要进行优化的函数；
   fun是一个接受向量x并返回向量F的函数，在x处计算目标函数， fun可以通过函数文件的函数句柄进行指定；例如x = fgoalattain(@myfun,x0,goal,weight)，其中，myfun就是MATLAB中的函数比如 ：function F = myfun(x)； F = ...，fun也可以是匿名函数的函数句柄，比如x = fgoalattain(@(x)sin(x.*x),x0,goal,weight)，其中的sin函数就是匿名函数；如果x和F的用户定义值是数组，则系统会使用线性索引将它们转换为向量。
   为了使目标函数尽可能接近目标值（即，既不大于也不小于），使用优化将EqualityGoalCount选项设置为需要在目标值附近的目标数量。 必须将这些目标划分为fun返回的向量F的第一个元素。
   如果也可以计算目标函数的梯度，并且SpecifyObjectiveGradient选项为true，则设置为options = optimoptions('fgoalattain','SpecifyObjectiveGradient',true)，那么函数fun必须在第二个输出参数中返回梯度值G，即x处的矩阵。 梯度由点x处的每个F的偏导数dF/dx组成。 如果F是长度为m且x长度为n的向量,其中n是x0的长度，则F(x)的梯度G是n×m矩阵，其中G(ij)是偏导数 F(j)相对于x(i)（即第j列的第j列是第j个目标函数F(j)的梯度)。
   <2>. goal:目标需要努力达到的向量的值。
   其中向量的长度与fun返回的目标向量F相同，fgoalattain尝试最小化向量F中的值以达到goal给出的目标值。
   <3>. nonlcon:计算约束条件中非线性不等式c（x）≤0和非线性等式ceq（x）= 0的函数；
   函数nonlcon接受向量x并返回两个向量c和ceq。 向量c包含在含有x的非线性不等式中，并且ceq包含在含有x的非线性等式中。 函数nonlcon可以通过函数句柄进行指定，比如x = fgoalattain(@myfun,x0,goal,weight,A,b,Aeq,beq,.. lb,ub,@mycon)，其中mycon就是nonlcon的函数，示例如下：function [c,ceq] = mycon(x) c = ... % compute nonlinear inequalities at x. ceq = ... % compute nonlinear equalities at x.
   <4>. options: 提供选项值的功能特定详细信息。
   <5>. weight: 加权矢量用于控制fgoalattain中目标的相对不足或超额数值。 当目标值全部为非零时，为了确保活动目标的低于或超过相同百分比，将加权函数设置为abs（goal);
   当加权函数权重为正时，fgoalattain会尝试使目标小于目标值。 要使目标函数大于目标值，请将权重设置为负值而不是正值。 要使目标函数尽可能接近目标值，请使用EqualityGoalCount选项并将该目标作为fun返回的向量的第一个元素（请参阅前面的fun和options描述）。
   <6>. problem:
   目标：目标函数的向量;
   x0：x的初始点；
   goal：需要实现的目标；
   weight：目标的相对重要性因素；
   Aineq：线性不等式约束的矩阵；
   bineq：线性不等式约束的向量；
   Aeq：用于线性等式约束的矩阵；
   beq：线性等式约束的向量；
   lb：下界矢量；
   ub：上界矢量；
   nonlcon：非线性约束函数；
   solve：‘fgoalattain’；
   options：使用optimoptions创建的选项；

6. 返回值详解
   <1>. attainfactor: 表征目标的过度或不足的程度。
   achiefactor包含解决方案中γ的值。 如果attainfactor是负的，那么设定的目标类似于过拟合; 如果attainfactor是正的，设定的目标便欠拟合。
   <2>. exitflag : 整数标识算法终止的原因。 以下列出了exitflag的值以及算法终止的相应原因。
   1：函数收敛到解x。
   4：搜索方向的幅度小于指定的容差和约束违规小于options.ConstraintTolerance
   5：方向导数的幅度小于指定的容差和约束违规小于options.ConstraintTolerance
   0：迭代次数超出options.MaxIterations或函数评估次数超出options.MaxFunctionEvaluations
   -1：由输出功能或绘图功能停止。
   -2：找不到可行点。
   <3>. lambda :在解x中包含拉格朗日乘数的结构（由约束类型分隔）。 结构的范围是：
   lower：下限lb
   upper：上限ub
   ineqlin：线性不等式
   eqlin：线性均衡
   ineqnonlin：非线性不等式
   eqnonlin：非线性等式
   <4>. output : 包含有关优化的信息的结构。 结构的范围是：
   iterations：迭代次数
   funcCount：函数评估的数量
   lssteplength：相对于搜索方向的最终行搜索步骤的大小
   stepize：x中的最终位移
   algorithm ：使用的优化算法
   firstorderopt：一阶最优性的度量
   constrviolation：约束函数的最大值
   message ：退出消息

7. 应用案例
   某工厂因生产需要欲采购一种原材料，市场上的这种原料有两个等级，甲级单价2元/千克，乙级单价1元/千克。要求所花总费用不超过200元，购得原料总量不少于100千克，其中甲级原料不少于50千克，问如何确定最好的采购方案。
   设x1、x2分别为采购甲级和乙级原料的数量（千克），要求采购总费用尽量少，采购总重量尽量多，采购甲级原料尽量多。由题意可得：
   首先需要编写目标函数的M文件lwj.m，返回目标计算值:

function f=myfun(x)
f(1)=2*x(1)+ x(2); % f(1)表示的是原料采购总费用
f(2)=-x(1)- x(2); % f(2)表示的是采购总重量
f(3)=-x(1); % f(3)甲级原料的总质量

给定目标，权重按目标比例确定，给出初值:
在这里要注意的地方时，fgoalattain函数以最小优化为目的，所以目标函数的数值目标（也就是下边的goal）是≤的时候，系数为+，目标函数是≥的时候，系数为-；

    goal=[200 –100 -50]; %goal中的数据表示f(1)，f(2)，f(3)各自的目标数值；
    weight=[2040 –100 -50]; %权重中的数值意义同上
    x0=[55 55]; %初始值x0可自己随意按照符合条件的数值进行设定【不是真的随心所欲】，此处55和55符合条件；

给出约束条件的系数:

A=[2 1;-1 –1;-1 0]; % 此处3*2矩阵A中的数值是目标函数的系数矩阵
b=[200 -100 -50]; % 目标函数结果的矩阵

lb=zeros(2,1); %限定条件

调用：

[x,fval,attainfactor,exitflag] =fgoalattain(@lwj,x0,goal,weight,A,b,[],[],lb,[]);  % 函数调用

输出计算结果:

x =
    50    50
fval =
   150  -100   -50
attainfactor =
  1.3235e-023
exitflag =
     1

所以，最好的采购方案是采购甲级原料和乙级原料各50千克。此时采购总费用为150元，总重量为100千克，甲级原料总重量为50千克。

如果觉得本文写的还不错的伙伴，可以给个关注一起交流进步，如果有在找工作且对阿里感兴趣的伙伴，也可以发简历给我进行内推：