DFS(深度优先搜索)详解———附例题
深度优先搜索属于图算法的一种,英文缩写为DFS即Depth First Search.其过程就是一个走迷宫的过程:
1.从顶点t出发,选择一个与t相连的未被访问过的顶点w。
2.然后从w出发,选择与w相连的一个未被访问过的顶点。
3.重复这个过程,每当到达一个其所有相邻的邻接顶点都已被访问过的顶点,就从该顶点开始,依次退回上一个顶点,直到到达尚有邻接顶点未曾被访问过的顶点u,并从u开始进行深度优先搜索。
4.直到所有顶点都被访问到为止,搜索过程结束。
这个算法通常可以用来解决全排列问题,迷宫问题,和在一个大数组中,寻找所有符合某一条件的集合的问题,下面分别针对这三个问题由浅入深地进行举例:
1.全排列问题:假如有编号为1、2、3的3张扑克牌和编号为1、2、3的3个盒子,现在需要将这3张扑克牌分别放到3个盒子里面,并且每个盒子有且只能放一张扑克牌。那么一共有多少种不同的做法呢?
不难看出,一共会出现6种排列,分别是:123、132、213、231、312、321。
下面Java代码来实现:
public class FullyArranged {
//往第idx个盒子里放卡片
private static void dfs(int idx, int[] boxs,int n,int[] book) {
// 检查是否这次搜索到了尽头
if(idx==n+1)
{
//print this combination
for(int j=1;j<=n;j++)
{System.out.print(boxs[j]);
}
System.out.print("\n");
//返回上一个dfs
return;}
//i 代表卡片,boxs代表盒子,idx代表第几个盒子,book用来标记这张牌是否还在手中(1=>已经分发,0=>仍然可以用)
//此时站在第idx个盒子面前,应该放哪张牌呢
//按照1、2、3...n的顺序一一尝试
for(int i=1;i<=n;i++)
{
//如果第i张卡片依然可用,则把他放到第idx个盒子里
if(book[i]==0)
{
boxs[idx]=i;
book[i]=1;
//第idx个盒子放完,接下来往第idx+1个盒子里放卡片
dfs(idx+1,boxs,n,book);
//走到这部说明这条分支已经结束,需要尝试下一条了
//所以取消这张卡片的标记
book[i]=0;
}
}
}
public static void main(String[] args) {
// TODO Auto-generated method stub
int n=3;
int[] boxs=new int[10];
int[] book=new int[10];
dfs(1,boxs,n,book);
}
}
2.迷宫问题:
假设一个迷宫如下,想要找出最快走出迷宫需要几步:
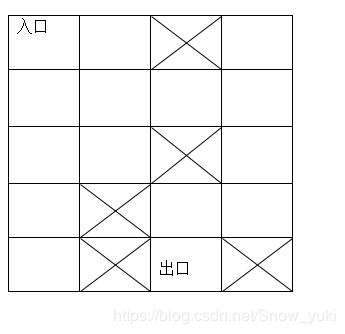
public class Maze {
static int min=9999;
private static void dfs(int x, int y,int step,int[][]book,int[][] m,int[][] next,int outx,int outy) {
int tx,ty;
//判断此个分支是否应该结束
if(x==outx&&y==outy) {
if(min>step)
{min=step;}
//返回最近上一个DFS
return ;
}
//在这个点依次尝试向上走,向下走,向左走,向右走
for(int i=0;i<=3;i++)
{
tx=x+next[i][0];
ty=y+next[i][1];
//判断当前位置是否还属于迷宫
if(tx<0||tx>4||ty<0||ty>3)
{continue;}
//如果这个点还没被走过,并且没有阻碍,则继续前行
if(m[tx][ty]==0&&book[tx][ty]==0)
{
//标记已经走过
book[tx][ty]=1;
//探索这个分支的下一步走向
dfs(tx,ty,step+1,book,m,next,outx,outy);
//走到这一步说明此路不通,清除标记
book[tx][ty]=0;
}
}
return;
}
public static void main(String[] args) {
//右,下,左,上
int next[][]={{0,1},{1,0},{0,-1},{-1,0}};
int m[][]={{0,0,1,0},{0,0,0,0},{0,0,1,0},{0,1,0,0},{0,1,0,1}};
int book[][]=new int[5][4];
book[0][0]=1;
dfs(0, 0, 0,book,m,next,4,2);
System.out.print(min);
}
minstep=8
3.在一个大数组中,寻找所有符合某一条件的集合的问题:
给一个整数数组和目标数,找到所有数组中数字总和为目标的子集。(同一个元素不可重复使用)。
package jkdh;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
public class ComSum {
public static List<List<Integer>> combinationSum(int[] candidates, int target) {
Arrays.sort(candidates);
List<List<Integer>> ret = new ArrayList<>();
dfs(candidates, target, 0, new ArrayList<>(), ret);
return ret;
}
private static void dfs(int[] candidates, int target, int idx, List<Integer> path, List<List<Integer>> ret) {
//检查一个分支是否应该结束
if (target <= 0) {
//如果符合条件,则把这个分支子集加到需要返回的总集里
if (target == 0) {
ret.add(path);
}
//返回最近的上一个一个dfs
return;
}
for (int i = idx; i < candidates.length; i++) {
List<Integer> p = new ArrayList<>(path);
//如果尝试到相同数字的不同子分支则跳过
//运行到i>idx说明i=idx这个节点走不通,在依此尝试不同的节点
if (i > idx && candidates[i] ==candidates[i-1]) {
continue;
}
p.add(candidates[i]);
//继续在这个分支上寻找下一个结点
dfs(candidates, target-candidates[i], i+1, p, ret);
}
}
public static void main(String[] args) {
// TODO Auto-generated method stub
List<List<Integer>> ret = new ArrayList<>();
int[] can=new int[]{10,1,2,7,6,1,5};
ret=combinationSum(can, 8);
System.out.print(ret);
}
}
对于半路出家的小码农我来说,以上就是我现在最经常遇到的三种dfs问题,dfs问题一开始遇到确实有点懵,绕来绕去搞不清原理,不过多做几个理清思维之后,就会发现全是套路,就是一个每条路我都要尝试,此路不通,退回来重新再试另外一条的方法。通常当遇到需要利用穷举方法才能解决的题时,最好尝试往dfs方面想,菜鸟总结完毕,如有错误或疑问,欢迎大家指出。