参考 problem solving with algorithms and data structures
细节注意
(1)Python 中 string类型不能重复赋值,string类型是不可变的。要实现str[1] = '3'的操作,可以先将string类型转为list。alist = list(str)
算法示例
(1)回文数判断
两个字符中组成字母一样只是位置不一样,则说这两个字符为回文字符。
判断回文字符有以下几种思路:给定字符串A中一个字母,看字符串B中是否有,如果有则置为None。可以看出算法复杂度为O(n**2);另一种思路就是先将字符串A和字符串B都进行排序,再依次进行对比,虽然可以简单调用sort()函数,但还是受限于排序本身的复杂度,为O(nlogn)或O(n^2)。最后一种算法可以实现线性,复杂度为O(n)。
def anagramSolution4(s1,s2):
c1 = [0]*26
c2 = [0]*26
for i in range(len(s1)):
pos = ord(s1[i])-ord('a')
c1[pos] = c1[pos] + 1
for i in range(len(s2)):
pos = ord(s2[i])-ord('a')
c2[pos] = c2[pos] + 1
j = 0
stillOK = True
while j<26 and stillOK:
if c1[j]==c2[j]:
j = j + 1
else:
stillOK = False
return stillOK
print(anagramSolution4('apple','pleap'))
(2)list性能分析
小片段代码运行时间分析-timeit模块
以下是几种常用的构造list方法,不同方法性能优劣要了解
from timeit import Timer
def test1():
l = []
for i in range(1000):
l = l + [i]
def test2():
l = []
for i in range(1000):
l.append(i)
def test3():
l = [i for i in range(1000)]
def test4():
l = list(range(1000))
t1 = Timer("test1()", "from __main__ import test1")
print("concat ",t1.timeit(number=1000), "milliseconds")
t2 = Timer("test2()", "from __main__ import test2")
print("append ",t2.timeit(number=1000), "milliseconds")
t3 = Timer("test3()", "from __main__ import test3")
print("comprehension ",t3.timeit(number=1000), "milliseconds")
t4 = Timer("test4()", "from __main__ import test4")
print("list range ",t4.timeit(number=1000), "milliseconds")
结果:
concat 1.7288866040762514 milliseconds
append 0.11190369189716876 milliseconds
comprehension 0.056128402007743716 milliseconds
list range 0.017755266977474093 milliseconds
字典中除了iteration的时间复杂度为O(n),其他的如get、set、in、delete方法的时间复杂度都是O(1),而列表list del操作为O(n)。
列表和字典in性能对比:
import timeit
import random
for i in range(10000,1000001,20000):
t = timeit.Timer("random.randrange(%d) in x"%i,
"from __main__ import random,x")
x = list(range(i))
lst_time = t.timeit(number=1000)
x = {j:None for j in range(i)}
d_time = t.timeit(number=1000)
print("%d,%10.3f,%10.3f" % (i, lst_time, d_time))
运行结果分析:
10000, 0.084, 0.001
30000, 0.262, 0.001
50000, 0.424, 0.001
70000, 0.579, 0.001
90000, 0.761, 0.001
110000, 0.928, 0.001
Timer类一般需要两个参数,第一个是需要测量的程序片,可以用‘;’分开,第二个参数是setup,即运行环境,上面每次导入x就很巧妙实现了一个函数测量不同的程序。
关于from import语句,有以下解释:
The setup statement may look very strange to you, so let’s consider it in more detail. You are probably very familiar with the
from, importstatement, but this is usually used at the beginning of a Python program file. In this case the statementfrom __main__ import test1imports the function test1 from the__main__namespace into the namespace that timeit sets up for the timing experiment. The timeit module does this because it wants to run the timing tests in an environment that is uncluttered by any stray variables you may have created, that may interfere with your function’s performance in some unforeseen way.
(3)数据结构之堆栈
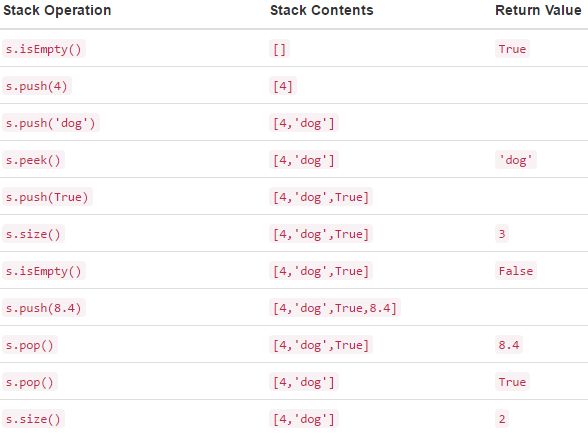
堆--后进先出,类似于桌上放书本在顺序取,后面放的先拿出来,在实际中也有很多应用,如网页的back操作,word中的撤销操作。关于stack的操作也比较简单,python中s = Stack()就可以创建一个空的stack,method有以下几种:
实际实现时可以用list,push操作等效为list的append,由于是list ,push 操作内容比较丰富,可以是各种类型,如字符串。
class Stack:
def __init__(self):
self.items = []
def isEmpty(self):
return self.items == []
def push(self, item):
self.items.append(item)
def pop(self):
return self.items.pop()
def peek(self):
return self.items[len(self.items)-1]
def size(self):
return len(self.items)
注意:The pythonds module contains implementations of all data structures discussed in this book. It is structured according to the sections: basic, trees, and graphs. The module can be downloaded from pythonworks.org.
带来很大方便,可以直接使用,例如:
from pythonds.basic.stack import Stack s=Stack()
stack应用举例
判断符号是否对称
from pythonds.basic.stack import Stack
def parChecker(symbolString):
s = Stack()
balanced = True
index = 0
while index < len(symbolString) and balanced:
symbol = symbolString[index]
if symbol in "([{":
s.push(symbol)
else:
if s.isEmpty(): #未考虑问题1
balanced = False
else:
top = s.pop()
if not matches(top,symbol):
balanced = False
index = index + 1
if balanced and s.isEmpty(): #未考虑问题2
return True
else:
return False
def matches(open,close):
opens = "([{"
closers = ")]}"
return opens.index(open) == closers.index(close)
print(parChecker('{{([][])}()}'))
print(parChecker('[{()]'))
上述程序为参考程序,实际自己写时会遇到很多问题,主要还是考虑不全面,比如自己写的犯了以下几个问题:一是没有考虑是否s为空,当输入']'就会出现问题;二是没有考虑是否全部匹配完成最终为空,当'{[[]]'就会出现问题。
上面程序其实可以简化
def parchecker(symbolstring):
s = []
match = {'(':')','[':']','{':'}'}
if symbolstring == '':
return False
for item in symbolstring:
if item in '{[(':
s.append(item)
elif len(s) == 0:
return False
else:
if s == [] or match[s.pop()] != item:
return False
return s == []
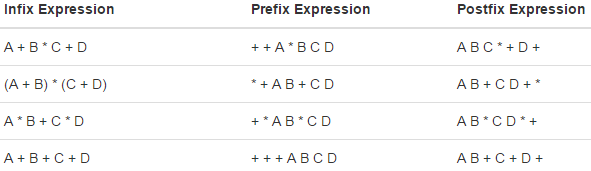
前缀、中缀、后缀表达式
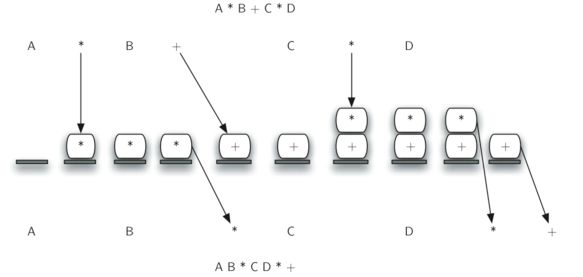
中缀表达式比较常见,主要分析中缀表达式和其他两种之间的转换。对于转换到后缀表达式,主要思想为:操作数位置相对不变,只是操作符的位置有变化,操作符位置基本原则就是看优先级,优先级高的在前先运算,同时考虑到带括号,括号内的运算符优先级最高。可是如何把这简单的思想写成程序,这也是最难的一步。
一个中缀表达式输入,要输出一个后缀表达式,首先要取出每个操作数和操作符,并挨个进行判断,当是操作数时直接append,如果是操作符要进行相应判断。值得注意的一点是如果待判断的符号优先级大于等于已进栈的优先级,则一直进栈,如果小于,则要循环判断出栈。
from pythonds.basic.stack import Stack
def infixToPostfix(infixexpr):
prec = {}
prec["*"] = 3
prec["/"] = 3
prec["+"] = 2
prec["-"] = 2
prec["("] = 1
opStack = Stack()
postfixList = []
tokenList = infixexpr.split()
for token in tokenList:
if token in "ABCDEFGHIJKLMNOPQRSTUVWXYZ" or token in "0123456789":
postfixList.append(token)
elif token == '(':
opStack.push(token)
elif token == ')':
topToken = opStack.pop()
while topToken != '(':
postfixList.append(topToken)
topToken = opStack.pop()
else:
while (not opStack.isEmpty()) and \
(prec[opStack.peek()] >= prec[token]):
postfixList.append(opStack.pop())
opStack.push(token)
while not opStack.isEmpty():
postfixList.append(opStack.pop())
return " ".join(postfixList)
print(infixToPostfix("A * B + C * D"))
print(infixToPostfix("( A + B ) * C - ( D - E ) * ( F + G )"))
队列
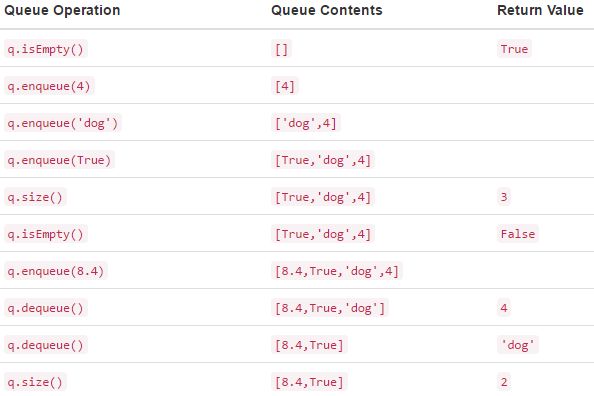
Queue()可以创建一个队列,有以下的methods,
Python中实现队列也可以使用list这个基本数据结构,进队列相当于在列表首位置插入,这里的复杂度为O(n),出队列的复杂度为O(1)。如下
class Queue:
def __init__(self):
self.items = []
def isEmpty(self):
return self.items == []
def enqueue(self, item):
self.items.insert(0,item)
def dequeue(self):
return self.items.pop()
def size(self):
return len(self.items)
队列应用
考虑一个场景,实验室有一台打印机,1小时之内有10个同学使用,每个同学平局使用两次,即180s会有一个任务,每次打印1-20页,而打印机的速率为每分钟打印5页,求出平均每个同学需要等待的时间。
more detail
from pythonds.basic.queue import Queue
import random
class Printer:
def __init__(self, ppm):
self.pagerate = ppm
self.currentTask = None
self.timeRemaining = 0
def tick(self):
if self.currentTask != None:
self.timeRemaining = self.timeRemaining - 1
if self.timeRemaining <= 0:
self.currentTask = None
def busy(self):
if self.currentTask != None:
return True
else:
return False
def startNext(self,newtask):
self.currentTask = newtask
self.timeRemaining = newtask.getPages() * 60/self.pagerate
class Task:
def __init__(self,time):
self.timestamp = time
self.pages = random.randrange(1,21)
def getStamp(self):
return self.timestamp
def getPages(self):
return self.pages
def waitTime(self, currenttime):
return currenttime - self.timestamp
def simulation(numSeconds, pagesPerMinute):
labprinter = Printer(pagesPerMinute)
printQueue = Queue()
waitingtimes = []
for currentSecond in range(numSeconds):
if newPrintTask():
task = Task(currentSecond)
printQueue.enqueue(task)
if (not labprinter.busy()) and (not printQueue.isEmpty()):
nexttask = printQueue.dequeue()
waitingtimes.append( nexttask.waitTime(currentSecond))
labprinter.startNext(nexttask)
labprinter.tick()
averageWait=sum(waitingtimes)/len(waitingtimes)
print("Average Wait %6.2f secs %3d tasks remaining."%(averageWait,printQueue.size()))
def newPrintTask():
num = random.randrange(1,181)
if num == 180:
return True
else:
return False
for i in range(10):
simulation(3600,5)
这个题虽然不是很难,但真正面向了实际的问题,很好体现了面向对象编程的思想,需要好好理解。
双向队列
与上述队列类似,只是双向队列可以从队列的任意一端进行操作。
创建一个双向队列。d = Deque()
关于双向队列的实现在Python中也可以利用列表这一基础的数据结构实现。
链表
list列表的实现可以是通过链表实现,链表实现的基础是节点node类,
class Node:
def __init__(self,initdata):
self.data = initdata
self.next = None
def getData(self):
return self.data
def getNext(self):
return self.next
def setData(self,newdata):
self.data = newdata
def setNext(self,newnext):
self.next = newnext
以下是一个完整的无序链表部分methods程序,值得注意为了标明链表的起始位置,都有一个head,head一直指向链表首部,每次都从头部插入。这里的add 方法实现值得借鉴,比较简单,每次新加入的node作为head。
class UnorderedList:
def __init__(self):
self.head = None
def isEmpty(self):
return self.head == None
def add(self,item):
temp = Node(item)
temp.setNext(self.head)
self.head = temp
def size(self):
current = self.head
count = 0
while current != None:
count = count + 1
current = current.getNext()
return count
def search(self,item):
current = self.head
found = False
while current != None and not found:
if current.getData() == item:
found = True
else:
current = current.getNext()
return found
# assume the item is present
def remove(self,item):
current = self.head
previous = None
found = False
while not found:
if current.getData() == item:
found = True
else:
previous = current
current = current.getNext()
if previous == None:
self.head = current.getNext()
else:
previous.setNext(current.getNext())
有序链表实现
相比之前的无序,有序链表实现有以下不同:
def search(self,item):
current = self.head
found = False
stop = False
while current != None and not found and not stop:
if current.getData() == item:
found = True
else:
if current.getData() > item:
stop = True
else:
current = current.getNext()
return found
def add(self,item):
current = self.head
previous = None
stop = False
while current != None and not stop:
if current.getData() > item:
stop = True
else:
previous = current
current = current.getNext()
temp = Node(item)
if previous == None:
temp.setNext(self.head)
self.head = temp
else:
temp.setNext(current)
previous.setNext(temp)
递归
递归算法的实质是把问题分解成规模缩小的同类问题的子问题,然后递归调用方法来表示问题的解。递归算法对解决一大类问题很有效,它可以使算法简洁和易于理解。递归算法,其实说白了,就是程序的自身调用。
经典的递归示例:
(1)计算阶乘
int factorial(int n){
if(n == 1)
return 1;
else
return n * factorial(n - 1);
}
(2)链表求和
int sum_list(struct list_node *l){
if(l == NULL)
return 0;
return l.data + sum_list(l.next);
}
递归函数可以和循环相互转化, 区别在于,使用递归函数极少被迫修改任何一个变量,只需要将新值作为参数传递给下一次函数调用。设计递归函数时,一定要注意函数出口,否则会一直循环下去。
(3)进制转换
def toStr(n,base):
convertString = "0123456789ABCDEF"
if n < base:
return convertString[n]
else:
return toStr(n//base,base) + convertString[n%base]
print(toStr(1453,16))
上述实现利用递归特别巧妙,膜拜啊。之前的做法一般为利用stack,将余数保留在stack中,在不断循环,对比
from pythonds.basic.stack import Stack
def baseConverter(decNumber,base):
digits = "0123456789ABCDEF"
remstack = Stack()
while decNumber > 0:
rem = decNumber % base
remstack.push(rem)
decNumber = decNumber // base
newString = ""
while not remstack.isEmpty():
newString = newString + digits[remstack.pop()]
return newString
print(baseConverter(25,2))
print(baseConverter(25,16))
两种方法思路一样,注意循环和递归之间一般来说可以相互转化,递归能大大减少代码量,注意实际应用。
(4)汉诺塔问题
分析可以参考
def moveTower(height,fromPole, toPole, withPole):
if height >= 1:
moveTower(height-1,fromPole,withPole,toPole)
moveDisk(fromPole,toPole)
moveTower(height-1,withPole,toPole,fromPole)
def moveDisk(fp,tp):
print("moving disk from",fp,"to",tp)
moveTower(3,"A","B","C")
主要有以下三个步骤:
- Move a tower of height-1 to an intermediate pole, using the final pole.
- Move the remaining disk to the final pole.
- Move the tower of height-1 from the intermediate pole to the final pole using the original pole.
递归的一些复杂问题需要一定时间理解.
可以先学习一下最简单的二叉树实现函数,函数中包含两个递归,以最简单的长度为30考虑,画出基本单元是一个‘Y’,两个地方递归调用了tree函数,第一次调用输入长度变为15,画右半边,最后返回到中心处,第二次调用画左半边,最后t.right(20)保证backward时方向为沿原来方向。最基本的画好,当长度增加时,如45,通过递归调用两次长度为30就好。
import turtle
def tree(branchLen,t):
if branchLen > 5:
t.forward(branchLen)
t.right(20)
tree(branchLen-15,t)
t.left(40)
tree(branchLen-15,t)
t.right(20)
t.backward(branchLen)
def main():
t = turtle.Turtle()
myWin = turtle.Screen()
t.left(90)
t.up()
t.backward(100)
t.down()
t.color("green")
tree(75,t)
myWin.exitonclick()
main()
(5)迷宫
http://interactivepython.org/courselib/static/pythonds/Recursion/ExploringaMaze.html
动态规划-Dynamic Programming
动态规划算法通常基于一个递推公式及一个或多个初始状态。当前子问题的解将由上一次子问题的解推出。
(1)凑数
从一个最简单的示例程序出发,有三种硬币分别为1,3,5,给定数字sum,求出最少需要的硬币数凑齐sum。
def main(sum):
L = [i for i in range(sum+1)]
coin = [1,3,5]
for i in range(1,sum+1):
for count in coin:
if i >= count and L[i-count] + 1 < L[i]:
L[i] = L[i-count] + 1
print '%d need %d' %(i , L[i])
main(11)
通过之前的状态计算当前。
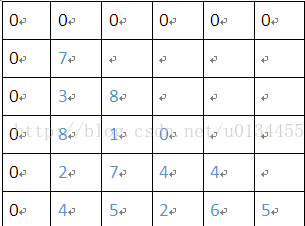
(2)数塔问题
由以上形状的数塔,要求出从顶至底经过数字和最大的一条路径。首先将问题形象化,将数据表示成而为数组,
最简单的最傻的方法就是遍历,都加一遍求出最大值,可以巧妙运用递归的方法,如下
def mymax(i,j):
if i == lenth or j == lenth:
return L[i][j]
left = mymax(i+1,j) + L[i][j]
right = mymax(i+1,j+1) + L[i][j]
return max(left,right)
if __name__ == '__main__':
L = [(7, 0, 0, 0, 0), (3, 8, 0, 0, 0), (8, 1, 0, 0, 0), (2, 7, 4, 4, 0), (4, 5, 2, 6, 5)]
lenth = len(L)-1
max = mymax(0,0)
print max
但方法不是最优,因为计算中还是存在冗余,考虑用DP进行完善。采用从底向上,计算出每个节点的最大值,并保存,当前节点的最大值直接利用上一节点数据进行计算。代码如下:
def mymax():
index = len(L)-1
for i in range(index-1,-1,-1):
for j in range(0,i+1):
L[i][j] += max(L[i+1][j] , L[i+1][j+1])
return L[0][0]
if __name__ == '__main__':
L = [[7, 0, 0, 0, 0], [3, 8, 0, 0, 0], [8, 1, 0, 0, 0], [2, 7, 4, 4, 0], [4, 5, 2, 6, 5]]
max = mymax()
print max
排序和查找
1、顺序查找较简单,略。
2、二分查找:
def binarysearch(L,item,low,high):
if length == 0:
return -1
mid = (low + high) // 2
if L[mid] == item:
return mid
else:
if L[mid] > item:
binarysearch(L,item,low,mid-1)
else:
binarysearch(L,item,mid+1,high)
if __name__ == '__main__':
L = [1,3,4,7,8,12,14,15,16,23,25,26,35,67]
length = len(L)
index = binarysearch(L,3,0,length)
print index
遇到一个小bug,要疯了。返回一直是none,程序做个小修改:
def binarysearch(L,item,low,high):
if length == 0:
return -1
mid = (low + high) // 2
if L[mid] == item:
return mid
else:
if L[mid] > item:
return(binarysearch(L,item,low,mid-1))
else:
return(binarysearch(L,item,mid+1,high))
def return_test():
return 2
if __name__ == '__main__':
L = [1, 3, 4, 7, 8, 12,14,15,16,23,25,26,35,67]
length = len(L)
index = binarysearch(L,67,0,length)
print index
现在结果正常了,对Python递归返回结果是None也是一个常遇到的问题,作简单分析。在迭代中,后调用的函数先返回,即最后一次调用会有正常返回ruturn mid,但是,前面的函数并没有要求返回值,Python中默认为none,故最终返回为none。
3、插值查找
基本思想就是不用每次固定对半查找,
mid=(low+high)/2, 即mid=low+1/2*(high-low);
通过类比,我们可以将查找的点改进为如下:
mid=low+(key-a[low])/(a[high]-a[low])*(high-low)
代码基本和上述一样。
4、hash查找
和上面查找稍有不同,
根据关键字直接进行访问的数据结构,把关键字通过hash算法映射到表中具体位置,可以加快查找速度。
哈希表的最简单实现。
class HashTable(object):
def __init__(self):
self.size = 11
self.slots = [None] * self.size
self.data = [None] * self.size
def put(self, key, data):
hashvalue = self.hashfunction(key, len(self.slots))
if self.slots[hashvalue] == None:
self.slots[hashvalue] = key
self.data[hashvalue] = data
else:
if self.slots[hashvalue] == key:
self.data[hashvalue] = data # replace
else:
nextslot = self.rehash(hashvalue, len(self.slots))
while self.slots[nextslot] != None and \
self.slots[nextslot] != key:
nextslot = self.rehash(nextslot, len(self.slots))
if self.slots[nextslot] == None:
self.slots[nextslot] = key
self.data[nextslot] = data
else:
self.data[nextslot] = data # replace
def hashfunction(self, key, size):
return key % size
def rehash(self, oldhash, size):
return (oldhash + 1) % size
def get(self, key):
startslot = self.hashfunction(key, len(self.slots))
data = None
stop = False
found = False
position = startslot
while self.slots[position] != None and \
not found and not stop:
if self.slots[position] == key:
found = True
data = self.data[position]
else:
position = self.rehash(position, len(self.slots))
if position == startslot:
stop = True
return data
def __getitem__(self, key):
return self.get(key)
def __setitem__(self, key, data):
self.put(key, data)
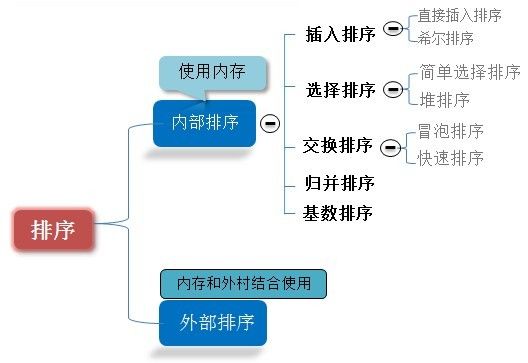
排序
上述内部排序中,目前是快速排序的效率最高
http://blog.csdn.net/column/details/algorithm-easyword.html 学习,通俗易懂
直接插入排序
思路很简单,就是每次取一个元素,往已经排好序的序列中插入
def insertSort(A):
for j in range(1, length):
key = A[j]
i = j - 1
while i >= 0 and A[i] > key:
A[i + 1] = A[i]
i = i - 1
A[i + 1] = key
return A
if __name__ == '__main__':
L = [23, 49, 18 ,6 ,74 ,53, 27]
length = len(L)
L = insertSort(L)
print L
另一种实现(C)
void Insertsort3(int a[], int n)
{
int i, j;
for (i = 1; i < n; i++)
for (j = i - 1; j >= 0 && a[j] > a[j + 1]; j--)
Swap(a[j], a[j + 1]);
}
希尔排序
和上一种排序方法同属于插入排序,希尔排序将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序,待整个序列中的记录“基本有序”时,再对全体记录进行依次直接插入排序。
希尔排序最关键的是选择步长,本程序选用Knuth在1969年提出的步长序列:1 4 13 40 121 364 1093 3280 。。。后一个元素是前一个元素*3+1
def shellSort(seq):
length=len( seq)
inc=0
while inc <= length/3:
inc = inc * 3 + 1
print inc
while inc >= 1:
for i in range(inc, length):
for j in range(i,0,-inc):
if seq[j] < seq[j-inc]:
seq[j], seq[j-inc] = seq[j-inc], seq[j]
inc//=3
if __name__ == '__main__':
seq = [8, 6, 4, 9, 7, 3, 2, - 4, 0, -100, 99]
shellSort(seq)
print(seq)
希尔排序整体思路比较简单,有三重循环,第一层循环是判断步长,最后一次的步长一定为1,第二层循环为从步长开始到序列尾,每次比较都根据步长分组,分组内进行直接插入排序,也就是从后往前两两比较。思路比较清楚。
简单选择排序
选择排序有简单选择排序,第1趟,在待排序记录r1 ~ r[n]中选出最小的记录,将它与r1交换;第2趟,在待排序记录r2 ~ r[n]中选出最小的记录,将它与r2交换;以此类推,第i趟在待排序记录r[i] ~ r[n]中选出最小的记录,将它与r[i]交换,使有序序列不断增长直到全部排序完毕。
def select_sort(lists):
# 选择排序
count = len(lists)
for i in range(0, count):
min = i
for j in range(i + 1, count):
if lists[min] > lists[j]:
min = j
lists[min], lists[i] = lists[i], lists[min]
return lists
简单选择排序的升级版-二元简单排序
def selectsort():
for i in range(0,length//2):
minindex = i
maxindex = i
for j in range(i+1,length):
if mylist[minindex] > mylist[j]:
minindex = j
if mylist[maxindex] < mylist[j] and j < length - i - 1:
maxindex = j
mylist[i],mylist[minindex] = mylist[minindex],mylist[i]
mylist[length-i-1],mylist[maxindex] = mylist[maxindex],mylist[length-i-1]
if __name__ == '__main__':
mylist = [23,34,12,34,87,2,31,55]
length = len(mylist)
selectsort()
print mylist
堆排序
堆排序有两步,一是将一个无序序列调整为一个堆,二是依次输出堆顶元素,将最后一个元素作为堆顶元素后再次调整为一个堆。
自定义实现
def heap_adjust(data, s, m):
temp = data[s]
j = 2 * s + 1
while j < m:
if j < m - 1 and data[j] < data[j + 1]:
j += 1
if temp > data[j]:
break
data[s] = data[j]
s = j
j = 2 * s + 1
data[s] = temp
def heap_sort(data):
m = len(data) / 2 - 1
for i in range(m, -1, -1):
heap_adjust(data, i, len(data) - 1)
for n in range(len(data) - 1, 0, -1):
data[0], data[n] = data[n], data[0]
heap_adjust(data, 0, n)
print data
Python中有一个模块heapq完成了堆排序的操作 参考
简单用法
from heapq import *
def heapsort(seq):
h = []
for item in seq:
heappush(h,item)
return [heappop(h) for i in range(len(h))]
if __name__ == '__main__':
seq = [8, 6, 4, 9, 7, 3, 2, - 4, 0, -100, 99]
seq = heapsort(seq)
print(seq)
更简单的方式为:
from heapq import *
if __name__ == '__main__':
seq = [8, 6, 4, 9, 7, 3, 2, - 4, 0, -100, 99]
# seq = heapsort(seq)
heapify(seq)
print(seq)
常用函数如下:
heapq.heappush(heap, item)
Push the value item onto the heap, maintaining the heap invariant.
heapq.heappop(heap)
Pop and return the smallest item from the heap, maintaining the heap invariant. If the heap is empty, IndexError is raised. To access the smallest item without popping it, use heap[0]
heapq.heappushpop(heap, item)
Push item on the heap, then pop and return the smallest item from the heap. The combined action runs more efficiently than heappush() followed by a separate call to heappop()
.
heapq.heapify(x)
Transform list x into a heap, in-place, in linear time.
heapq.heapreplace(heap, item)
和上面的heappushpop()类似,只是上面的是先压入一个数据到堆中,在从中pop出最小数,而heapreplace()则是先弹出最小数,再压入一个数据,在定长的堆操作中很有用。
归并排序
def mergesort(seq):
"""归并排序"""
if len(seq) <= 1:
return seq
mid = len(seq) / 2 # 将列表分成更小的两个列表
# 分别对左右两个列表进行处理,分别返回两个排序好的列表
left = mergesort(seq[:mid])
right = mergesort(seq[mid:])
# 对排序好的两个列表合并,产生一个新的排序好的列表
return merge(left, right)
def merge(left, right):
"""合并两个已排序好的列表,产生一个新的已排序好的列表"""
result = [] # 新的已排序好的列表
i = 0 # 下标
j = 0
# 对两个列表中的元素 两两对比。
# 将最小的元素,放到result中,并对当前列表下标加1
while i < len(left) and j < len(right):
if left[i] <= right[j]:
result.append(left[i])
i += 1
else:
result.append(right[j])
j += 1
result += left[i:]
result += right[j:]
return result
seq = [5,3,0,6,1,4]
print '排序前:',seq
result = mergesort(seq)
print '排序后:',result
偷个懒,程序完全转自 http://www.jianshu.com/p/3ad5373465fd
heapq模块中有个merge method,使用如下。该函数将两个已经有序的序列进行合并。
from heapq import merge
def merge_sort(seq):
if len(seq) <= 1:
return m
else:
middle = len(seq)/2
left = merge_sort(seq[:middle])
right = merge_sort(seq[middle:])
return list(merge(left, right)) #heapq.merge()
if __name__=="__main__":
seq = [1,3,6,2,4]
print merge_sort(seq)
快速排序
代码参考
快排和归并有很多相通的地方,归并是将一个序列不断划分为两半,靠merge函数将其排序,而快速排序划分是通过选取一个基数通过大小比较不断进行划分。两者都使用了递归的思想。
def qsort(list):
if not list:
return []
else:
pivot = list[0]
less = [x for x in list if x < pivot]
more = [x for x in list[1:] if x >= pivot]
return qsort(less) + [pivot] + qsort(more)
另一种实现
from random import *
def qSort(a):
if len(a) <= 1:
return a
else:
q = choice(a) #基准的选择不同于前,是从数组中任意选择一个值做为基准
return qSort([elem for elem in a if elem < q]) + [q] * a.count(q) + qSort([elem for elem in a if elem > q])
上面两个方法只是基数的选取不一样。
qs = lambda xs : ( (len(xs) <= 1 and [xs]) or [ qs( [x for x in xs[1:] if x < xs[0]] ) + [xs[0]] + qs( [x for x in xs[1:] if x >= xs[0]] ) ] )[0]
这个真是碉堡了
排序扩展
桶排序
桶排序是一种典型的以空间换时间的排序方法,其实在文章开始的回文数判断就已经用到了这种方法。
桶排序也有很多限制,比如一般需要预先知道排序数的范围。简单示例:
class BucketSort(object):
def __init__(self, datas, size=100):
self.datas = datas
self.bucketSize = size
self.result = [0 for i in range(len(datas))]
self.bucket = [0 for i in range(self.bucketSize)]
def _sort(self):
for num in self.datas:
self.bucket[num] += 1
j = 0
for i in range(self.bucketSize):
while (self.bucket[i]):
self.result[j] = i
self.bucket[i] -= 1
j += 1
def show(self):
print "Resutl is:",
for i in self.result:
print i,
print ''
if __name__ == '__main__':
datas = [1,2,5, 7, 6, 45,23, 67, 13, 88]
bks = BucketSort(datas)
bks._sort()
bks.show()
计数排序
def countingSort(alist,k):
n=len(alist)
b=[0 for i in xrange(n)]
c=[0 for i in xrange(k+1)]
for i in alist:
c[i]+=1
for i in xrange(1,len(c)):
c[i]=c[i-1]+c[i]
for i in alist:
b[c[i]-1]=i
c[i]-=1
return b
if __name__=='__main__':
a=[random.randint(0,100) for i in xrange(100)]
print countingSort(a,100)
基数排序
import random
def radixSort():
A=[random.randint(1,9999) for i in xrange(10000)]
for k in xrange(4): #4轮排序
s=[[] for i in xrange(10)]
for i in A:
s[i/(10**k)%10].append(i)
A=[a for b in s for a in b]
return A