知识图谱嵌入(KGE)主流模型简介
1. KGE简介
目前(2020.03)知识图谱嵌入研究方法众多,本文将对其中的主流方法进行简要介绍,如翻译、双线性、神经网络、双曲几何、旋转等。各方法细节请看原论文,文中错误欢迎指出,谢谢。
知识图谱嵌入(Knowledge Graph Embedding, KGE)学习知识库中的实体和关系的Embedding表示,是语义检索、知识问答、推荐等众多应⽤的基础研究。在具体了解KGE之前,我们先来看知识图谱是什么,为什么又要做知识图谱嵌入呢。
如下图所示,知识图谱是由大量的事实三元组组成,如(英国, 首都, 伦敦)便是真实世界中的知识,可用 ( h , r , t ) (h, r, t) (h,r,t)进行表示,其中 h , t h, t h,t表示头尾实体, r r r表示关系。但我们知道,真实世界中知识是无限增长的,而知识图谱却不能包含真实世界中的所有知识,因此需在知识库中进行知识补全,或者称为链接预测。
如何进行链接预测呢?一个可行的方法便是将实体和关系进行Embedding表示,类似于Word2Vec,将字或词表示成Embedding信息。然后根据实体和关系的Embedding信息进行预测,比如利用头实体和关系去预测尾实体,或者利用尾实体和关系去预测头实体。当然,Embedding信息也可应用到其他领域,比如知识问答、文本信息增强、语义检索等。
2. KGE模型
通过上面介绍,我们知道KGE是将知识库中的实体和关系进行Embedding表示,但具体有哪些方法呢?根据我个人的理解,将模型规划为翻译(TransE, TransH, TransR, etc)、双线性(RESCAL, DisMult, ComplEx, etc)、双曲几何(Poincare, MuRE, etc)、神经网络(ConvE, CapsE, etc)、旋转(RotatE, QuatE, DihEdral, etc)类别,下面逐一进行介绍。
2.1 翻译模型
翻译模型是把关系当作头实体和尾实体之间的翻译,包括TransE, TransH, TransD等模型。
TransE认为 h + r ≈ t h + r \approx t h+r≈t,即 r r r是头尾实体之间的翻译关系,并定义评分函数为 f r ( h , t ) = ∣ ∣ h + r − t ∣ ∣ 2 2 f_r(h, t) = ||h + r - t||_{2}^{2} fr(h,t)=∣∣h+r−t∣∣22,优化目标是最小化评分函数。TransE能够解决1-1类别的关系,但不能够很好的解决1-N, N-1, N-N关系。比如(流浪地球,演员,吴京)、(流浪地球,演员,吴孟达)两个三元组,当头实体 h h h和关系 r r r相同时,TransE认为所有尾实体 t t t具有相同的Embedding信息,但实际情况并非如此。
针对TransE存在的问题,TransH把头实体 h h h和尾实体 t t t投影到关系所在的超平面中,并定义评分函数为 f r ( h , t ) = ∣ ∣ h ⊥ + r − t ⊥ ∣ ∣ 2 2 f_r(h,t) = ||h_{\perp} + r - t_{\perp}||_{2}^{2} fr(h,t)=∣∣h⊥+r−t⊥∣∣22,其中 h ⊥ = h − w r T h w r , t ⊥ = t − w r T t w r h_{\perp} = h - w_{r}^{T}hw_{r}, t_{\perp} = t - w_{r}^{T}tw_{r} h⊥=h−wrThwr,t⊥=t−wrTtwr。经过投影后,尽管头实体 h h h和关系 r r r相同,尾实体 t t t的Embedding信息也会不同,TransH能够一定程度上解决多对多的关系。
TransR认为TransE和TransH均是把实体和关系放在同一空间中进行考虑,但实体可能具有多个不同方面的属性,不同的关系也关注着实体的不同属性,因此把实体和关系放在同一空间中考虑是不准确的。因此,TransR构建实体空间和关系空间,并定义评分函数为 f r ( h , t ) = ∣ ∣ h ⊥ + r − t ⊥ ∣ ∣ 2 2 f_{r}(h, t) = ||h_{\perp} + r - t_{\perp}||_{2}^{2} fr(h,t)=∣∣h⊥+r−t⊥∣∣22,其中 h ⊥ = h M r , t = t M r h_{\perp} = hM_{r}, t = t M_r h⊥=hMr,t=tMr, h ⊥ , t ⊥ h_{\perp}, t_{\perp} h⊥,t⊥属于实体空间, r r r属于关系空间。
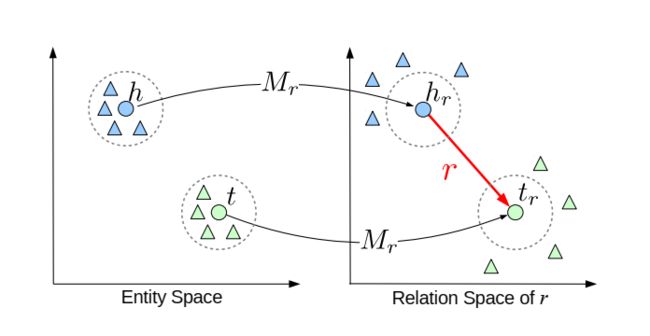
如下图所示,除了TransE, TransH, TransR以外,还有其他Trans模型,考虑实体和关系的概率性、稀疏性等问题,此处不再赘述。但总体上,Trans模型均是把关系当作头尾实体之间的翻译,解决知识库中所存在的多对多问题。

2.2 双线性模型
双线性模型计算实体和关系在向量空间中潜在语义的可信度,包括RESCAL、DisMult、ComplEx等模型。
RESCAL把关系利用满秩矩阵表示,并定义评分函数为 f r ( h , t ) = h T M r t f_r(h, t) = h^TM_rt fr(h,t)=hTMrt。能够看到,RESCAL的实体和关系之间全是矩阵运算,因此实体和关系的信息可以进行深层次交互,非常具有表现力。但同时,RESCAL容易过拟合,并且随着关系矩阵维度的增加,复杂度会很高,很难应用到大规模知识图谱。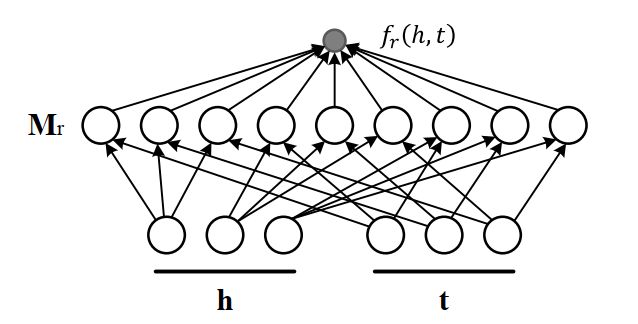
针对RESCAL存在的问题,DisMult放松对关系矩阵的约束,把关系矩阵 M r M_r Mr利用对角矩阵表示,并定义损失函数为 f r ( h , t ) = h T d i a g ( M r ) t f_{r}(h,t) = h^Tdiag(M_r)t fr(h,t)=hTdiag(Mr)t。但DisMult过分简化了RESCAL模型,导致只能够解决知识库中存在的对称关系,不能够解决知识图谱中其他类型的关系。
针对DisMult存在的问题,ComplEx把DisMult扩展到复数空间表示,并定义评分函数为 f r ( h , t ) = R e ( h T d i a g ( M r ) t ˉ ) f_{r}(h,t) = Re(h^Tdiag(M_r)\bar{t}) fr(h,t)=Re(hTdiag(Mr)tˉ),其中 h , t h, t h,t均用复数表示, t ˉ \bar{t} tˉ表示 t t t的共轭复数, R e ( ⋅ ) Re(\cdot) Re(⋅)表示取得复数的实部。ComplEx对DisMult扩展后,能够同时解决对称和非对称关系。ComplEx首次在KGE中引入复数方法,后面我们还能看到其他模型利用复数空间解决问题,并且可解决除对称、非对称外更复杂的对称类型。
如下图所示,除RESCAL, DisMult, ComplEx外,还有其他双线性模型,考虑实体和关系的潜在语义信息,获取实体和关系的深层次交互信息。

2.3 神经网络模型
多数翻译模型和双线性模型是16年之前模型,最近几年随着神经网络的兴起,也有利用神经网络解决KGE问题的模型,包括ConvE、CapsE等。
如下图所示,ConvE首先把头实体和关系转换为二维向量,接下来利用卷积层和全连接层获取交互信息,然后与矩阵 W W W和尾实体进行计算,判断当前三元组的可信度。ConvE评分函数为 f ( v e c ( f ( [ h ˉ , r ˉ ] ∗ w ) ) W ) t f(vec(f([\bar{h}, \bar{r}] * w ))W) t f(vec(f([hˉ,rˉ]∗w))W)t, h ˉ , r ˉ \bar{h}, \bar{r} hˉ,rˉ表示二维向量, w w w表示卷积核, W W W表示矩阵。ConvE模型上没什么新颖之处,只不过是比较早的利用卷积神经网络来对KGE进行建模。

如下图所示,CapsE采用胶囊神经网络模型,首先把头实体、关系、尾实体表示称 k × 3 k\times 3 k×3的矩阵,接下来通过卷积层获取其特征信息,然后对特征信息进行压缩,并进行动态路由,最后计算三元组的可信度,胶囊网络资料可参考苏神博客。CapsE只是胶囊网络在KGE问题上的简单应用,也没有特别新颖之处。

如下图所示,KG-BERT模型利用BERT进行fine-tuning,获取头实体、关系、尾实体信息,然后取CLS信息进行二分类,判断当前三元组可信度。

KGE除了利用卷积神经网络、胶囊网络、BERT模型外,也有模型利用深度神经网络、图注意力网络等方法,但均没有进行深层次扩展。个人认为,普通的神经网络模型不是特别适合解决KGE问题,不能够对知识图谱中实体的层次性、关系的多样性问题建模,仅仅只是获取实体和关系的深层次交互信息,没有可解释性。但可以多尝试图神经网络在KGE上的应用,比较符合图谱结构。
2.4 双曲几何模型
上面多次提到实体间具有层次性,比如爷爷–父亲–儿子关系,类似于树状结构。此时,可以利用双曲空间性质,在双曲空间中对实体的层次性建模,包括Poincare, MuRP等模型。
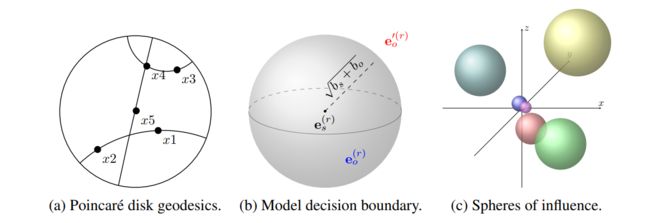
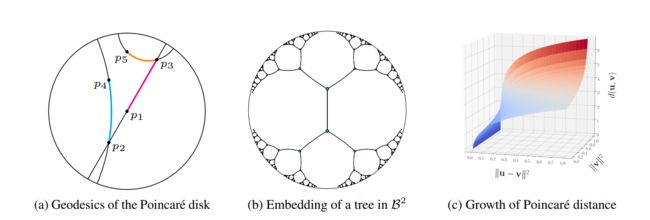
Poincare采用双曲几何中的庞加莱圆盘进行建模,其空间曲率为负。通过下图我们可以简单了解庞加莱圆盘性质,如下图(1)所示,是庞加莱圆盘中的测地线,可看作直线在双曲空间中的推广。如图(2)所示,图中每两个点之间线代表的长度是相同的。也就是说,离中心越远, 单位欧几里得空间的线段所代表的长度越长。如图(3)所示,当 ∣ ∣ u ∣ ∣ 2 ||u||^{2} ∣∣u∣∣2和 ∣ ∣ v ∣ ∣ 2 ||v||^{2} ∣∣v∣∣2趋近于1时,距离会变得无限大。双曲空间中两点之间距离计算方法为
d ( h , t ) = a r c o s h ( 1 + 2 ∣ ∣ h − t ∣ ∣ 2 2 ( 1 − ∣ ∣ h ∣ ∣ 2 2 ) ( 1 − ∣ ∣ t ∣ 2 2 ∣ ) ) d(h, t) = arcosh(1 + 2 \frac{||h - t||_{2}^{2}}{(1-||h||_{2}^{2})(1-||t|_{2}^{2}|)}) d(h,t)=arcosh(1+2(1−∣∣h∣∣22)(1−∣∣t∣22∣)∣∣h−t∣∣22)
因为庞加莱圆盘性质,能够对实体间的层次性建模,学习图谱间的层次性信息。Poincare模型评分函数为 f r ( h , t ) = ∑ ( h , t ) ∈ D l o g e − d ( h , t ) ∑ t ′ e − d ( h , t ′ ) f_{r}(h,t) = \sum_{(h,t) \in D} log \frac{e^{-d(h, t)}}{\sum_{t'}e^{-d(h, t')}} fr(h,t)=∑(h,t)∈Dlog∑t′e−d(h,t′)e−d(h,t),其中 ( h , t ′ ) (h,t') (h,t′)为负样本,其目标是让相关联的三元组在庞加莱圆盘中具有更小的距离。但Poincare模型没有考虑到关系性质,而且不能够在庞加莱圆盘中进行复杂操作。另外,双曲空间需要黎曼优化方法,建议自行去了解相关数学知识,包括黎曼曲率张量、黎曼流形、黎曼优化等概念。
MuRP相对于Poincare而言更加完善,MuRP同时在双曲空间和欧式空间中建模,结合关系向量,能够处理图谱中所存在的多类型关系。MuRP首先将实体向量定义在庞加莱圆盘中,接下来将实体映射到欧式空间,并和关系进行操作,然后再将实体映射回庞加莱圆盘中进行距离计算,并用黎曼方法优化。MuRP评分函数为 f r ( h , t ) = − d B ( e x p 0 c ( R l o g 0 c ( h ) ) , r ⊕ c t ) 2 + b h + b t f_{r}(h,t) = -d_{\mathbb{B}}(exp_{0}^{c}(Rlog_{0}^{c}(h)), r\oplus_{c}t)^2 + b_h + b_t fr(h,t)=−dB(exp0c(Rlog0c(h)),r⊕ct)2+bh+bt,其中 d B d_{\mathbb{B}} dB表示在庞加莱圆盘中计算距离, l o g 0 c ( ⋅ ) log_{0}^{c}(\cdot) log0c(⋅)表示将庞加莱圆盘中的点映射到欧式空间, R R R表示对角矩阵, e x p 0 c ( ⋅ ) exp_{0}^{c}(\cdot) exp0c(⋅)表示将欧式空间中的点转移到庞加莱圆盘中, ⊕ c \oplus_c ⊕c是莫比乌斯加法,为庞加莱空间中两向量相加, c c c表示曲率。另外, b h , b t b_h, b_t bh,bt表示头尾实体的偏置,如下图(2)所示,距离在 ( b h + b t ) \sqrt{(b_h + b_t)} (bh+bt)内均为正确的三元组。
d B = 2 c t a n h − 1 ( c ∣ ∣ − x ⊕ c y ∣ ∣ ) d_{\mathbb{B}} = \frac{2}{\sqrt{c}}tanh^{-1}(\sqrt{c}||-x\oplus_cy||) dB=c2tanh−1(c∣∣−x⊕cy∣∣)
x ⊕ c y = ( 1 + 2 c < x , y > + c ∣ ∣ y ∣ ∣ 2 ) x + ( 1 − c ∣ ∣ x ∣ ∣ 2 ) y 1 + 2 c < x , y > + c 2 ∣ ∣ x ∣ ∣ 2 ∣ ∣ y ∣ ∣ 2 x\oplus_c y = \frac{(1+2c
e x p x c ( v ) = x ⊕ c ( t a n h ( c λ x c ∣ ∣ v ∣ ∣ 2 ) v c ∣ ∣ v ∣ ∣ ) exp_{x}^c(v) = x\oplus_c \left(tanh\left(\sqrt{c} \frac{\lambda_x^c||v||}{2}\right)\frac{v}{\sqrt{c}||v||}\right) expxc(v)=x⊕c(tanh(c2λxc∣∣v∣∣)c∣∣v∣∣v)
l o g x c ( y ) = 2 c λ x c t a n h − 1 ( c ∣ ∣ − x ⊕ c y ∣ ∣ ) − x ⊕ c y − x ⊕ c y log_x^c(y) = \frac{2}{\sqrt{c}\lambda_x^c}tanh^{-1} (\sqrt{c}||-x\oplus_c y||)\frac{-x\oplus_cy}{-x\oplus_cy} logxc(y)=cλxc2tanh−1(c∣∣−x⊕cy∣∣)−x⊕cy−x⊕cy
通过Poincare和MuRP模型能够看出,双曲空间对于数学要求比较高,但双曲几何确实能够对图谱进行层次性信息建模,解决实体间的多类型关系。除了利用双曲空间中的庞加莱圆盘外,还有的模型利用李群、李代数等知识,此处不再赘述。数学较好的同学,可以深层次的研究双曲空间在KGE问题上的应用。
2.5 旋转模型
旋转模型把关系当作头实体和尾实体之间的旋转,包括RotatE、QuatE、DihEdral等模型。
RotatE认为知识库中存在多种类型的关系,如symmetry(e.g., marriage), antisymmetry(e.g., filiation), inversion(e.g., hypernym and hyponym), composition(e.g., my mother’s husband is my father)关系,但以往的TransE, RESCAL, ConvE等模型均不能够解决上述关系。因此,如下图(2)所示,RotatE提出在复数空间中建模,把关系当作头尾实体之间的旋转,并定义评分函数为 f r ( h , t ) = ∣ ∣ h ∘ r − t ∣ ∣ f_{r}(h,t) = ||h\circ r - t|| fr(h,t)=∣∣h∘r−t∣∣,其中 { h , r , t } = e i θ = c o s θ + i s i n θ \{h,r,t\} = e^{i\theta} = cos\theta + i sin \theta {h,r,t}=eiθ=cosθ+isinθ,RotatE从理论上证明能够解决对称/反对称、翻转、组合关系。另外,RotatE认为在训练过程中,很多三元组明显是错误的,因此RotatE提出自对抗的负采样方法,让错误样本更加明显,负采样和损失函数公式如下所示。
p ( h j ′ , r , t j ′ ∣ { ( h i ′ , r , t i ′ ) } ) = e x p ( α ∗ f r ( h j ′ , t j ′ ) ) ∑ i e x p ( α ∗ f r ( h i ′ , t i ′ ) ) p(h_{j}^{'}, r, t_{j}^{'}|\{(h_i^{'}, r, t_i^{'})\}) = \frac{exp (\alpha*f_r(h_j', t_j'))}{\sum_iexp(\alpha*f_r(h_i', t_i'))} p(hj′,r,tj′∣{(hi′,r,ti′)})=∑iexp(α∗fr(hi′,ti′))exp(α∗fr(hj′,tj′))
L = − l o g σ ( γ − f r ( h , t ) ) − ∑ i = 1 n p ( h i ′ , r , t i ′ ) l o g σ ( f r ( h i ′ , t i ′ ) − γ ) \mathbb{L} = -log\sigma(\gamma - f_r(h, t)) - \sum_{i=1}^{n} p(h_{i}^{'}, r, t_{i}^{'})log \sigma(f_r(h_{i}', t_{i}') - \gamma) L=−logσ(γ−fr(h,t))−i=1∑np(hi′,r,ti′)logσ(fr(hi′,ti′)−γ)

RotatE是在二维复平面空间中进行操作,那么很自然的可以推广到三维复平面空间中。三维情况下旋转可以利用欧拉角和四元数等方法,但欧拉角存在死锁问题,因此QuatE采用四元数进行旋转,四元数可表示为 Q = a + b i + c j + d k Q = a + bi + cj + dk Q=a+bi+cj+dk。QuatE定义评分函数为 f r ( h , t ) = h ⊗ r ◃ ⋅ t f_{r}(h, t) = h \otimes r^{\triangleleft} \cdot t fr(h,t)=h⊗r◃⋅t,其中 h , r , t h, r, t h,r,t均为四元数, r ◃ r^{\triangleleft} r◃表示 r r r的norm值, ⊗ \otimes ⊗表示Hamilton product, ⋅ \cdot ⋅表示内积。当然,继续推广,可以利用8元数进行旋转,但此时复杂度升高,结果并没有提升太多。再往上推广,有16元数,但16元数的乘法不满足交换律和结合律,因此不再考虑。
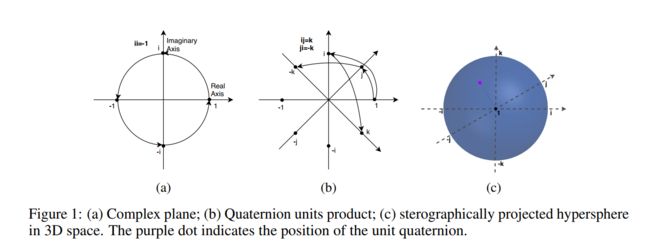
除了RotatE和QuatE利用复数空间解决对称/反对称、翻转、组合关系,DihEdral利用群论知识来解决上述关系。DihEdral采用二面体群进行旋转,如下图所示,二面体群具有两种性质,即旋转和对称操作。DihEdral将多个二面体群组成对角矩阵,并定义评分函数为 f r ( h , t ) = ∣ ∣ R T h − t ∣ ∣ 2 2 f_r(h, t) = ||R^Th - t||_{2}^{2} fr(h,t)=∣∣RTh−t∣∣22,其中 R R R是二面体群组成的对角矩阵,具体构建方法可以看原论文。同样,DihEdral能够从理论上解决对称/反对称、翻转、组合(Abelian, Non-Abelian)关系,如果对群论比较熟悉的同学,可以继续扩展,从群论+旋转+多类型关系的角度来解决KGE问题。

通过RotatE、QuatE、DihEdral模型能够看出,均是利用旋转特性来解决知识库中存在的对称/反对称、翻转、组合关系,但知识库中不仅仅存在这几种关系,还可以继续挖掘其他关系。同时,还可以继续研究其他旋转方法来解决KGE问题,比如群论方向,因为图谱完美符合群论的四个性质。
2.6 其他模型
除了上述介绍的翻译、双线性、神经网络、双曲几何、旋转模型外,还有的模型从路径、距离度量等角度去解决KGE问题,此处不再赘述。
3.总结
从上面介绍的模型可以看出,KGE问题可首先关注如下方面:
- 关系的多样性,如1-1, 1-N, N-1, N-N关系,对称/反对称、翻转、组合等信息。如翻译、旋转模型。
- 实体的层次性,实体之间的上下位关系。如双曲空间模型。
- 实体和关系的深层次交互信息。如双线性和神经网络模型。
除此之外,个人认为可深入研究的点包括图神经网络、欧式或双曲空间中实体的层次性问题、旋转模型解决关系多样性(群论角度)。同时,还需要重点关注负采样方法、损失函数、数据增强问题(比如(h, r, t)可扩展增加(t, r_inverse, h))。
文中所介绍到的论文如下所示,多数模型的代码都可在原论文中找到。如果想要使用已训练好的Wikidata, Freebase的Embedding信息,可以从清华OpenKE网站下载,个人训练的话可以使用OpenKE项目。
[1]: Translating Embeddings for Modeling Multi-relational Data “TransE”
[2]: Knowledge Graph Embedding by Translating on Hyperplanes “TransH”
[3]: Learning Entity and Relation Embeddings for Knowledge Graph Completion “TransR”
[4]: A Three-Way Model for Collective Learning on Multi-Relational Data “RESCAL”
[5]:Embedding entities and relations for learning and inference in knowledge bases “DisMult”
[6]: Complex embeddings for simple link prediction “ComplEx”
[7]: Convolutional 2D Knowledge Graph Embeddings “ConvE”
[8]: A Capsule Network-based Embedding Model for Knowledge Graph Completion and Search Personalization “CapsE”
[9]: KG-BERT: BERT for Knowledge Graph Completion “KG-BERT”
[10]: Poincare Embeddings for Learning Hierarchical Representations “Poincare”
[11]: Multi-relational Poincaré Graph Embeddings “MuRP”
[12]: ROTATE: KNOWLEDGE GRAPH EMBEDDING BY RELATIONAL ROTATION IN COMPLEX SPACE “RotatE”
[13]: Quaternion Knowledge Graph Embeddings “QuatE”
[14]: Relation Embedding with Dihedral Group in Knowledge Graph “DihEdral”