2020.01.12日常总结

$$洛谷P2564[SCOI2009]生日礼物$$

$【题意】：$ 小西有一条很长的彩带，彩带上挂着各式各样的彩珠。已知彩珠有$N$个，分为$K$种。简单的说，可以将彩带考虑为$x$轴，每一个彩珠有一个对应的坐标（即位置）。某些坐标上可以没有彩珠，但多个彩珠也可以出现在同一个位置上。

小布生日快到了，于是小西打算剪一段彩带送给小布。为了让礼物彩带足够漂亮，小西希望这一段彩带中能包含所有种类的彩珠。同时，为了方便，小西希望这段彩带尽可能$短$，你能帮助小西计算这个最短的长度么？彩带的长度即为彩带开始位置到结束位置的位置差。

$【思路】：$ 尺取法（Two-pointer）法的模板题。

具体地说，就是利用两个指针$l,r$，$l$表示当前扫描的区间的左端点，$r$表示右端点。如果区间$[l,r]$内有所有种类的珠子的话，我们用区间$[l,r]$的长度$更新$答案，并且尝试缩短区间$[l,r]$的长度（就是把与第$l$个珠子在同一位置上的珠子和它自己删除）。否则，我们把所有与第$r$个珠子在同一位置上的珠子和第$r$个珠子自己加入候选队列。

$时间复杂度：$因为每个珠子最多加入一次候选队列，且最多被删除一次，所以总的时间复杂度为$O(N)$。当然，我们需要排序，所以时间复杂度为$O(N\times logN)$。

$【代码】：$

#define gc getchar()
#define g(c) isdigit(c)
inline int read(){
	char c=0;int x=0;bool f=0;
	while (!g(c)) f=c=='-',c=gc;
	while (g(c)) x=x*10+c-48,c=gc;
	return f?-x:x;
}
const int N=1001000;
struct Bead{
	int position,color;
	bool operator < (Bead c) const{
		return position<c.position;
	}
}a[N];int cnt[100],n,m,tot,l,r,ans;
inline void Insert(int pos){
	if (cnt[a[pos].color]==0)
		tot++;//珠子总数加一 
	cnt[a[pos].color]++;
}//Insert the bead pos.
inline void Delete(int pos){
	cnt[a[pos].color]--;
	if (cnt[a[pos].color]==0)
		tot--;//珠子总数减一 
}//Delete the bead pos.
int main(){
	n=read();m=read();ans=1e9;
	for(int i=1;i<=m;i++){
		register int N=read();
		for(int j=1;j<=N;j++){
			a[++tot].color=i;
			a[tot].position=read();
		}
	}
	sort(a+1,a+n+1);l=r=1;
	memset(cnt,0,sizeof(cnt));
	cnt[a[1].color]=1;tot=1;
	for(int i=2;i<=n;i++)
		if (a[i].position==a[i-1].position){
			Insert(i);r++;
		}
		else break;
	while (l<=n&&r<=n){
		if (tot==m){
			ans=min(ans,a[r].position-a[l].position);
			Delete(l);++l;//Try to delete l to let ans be smaller.
			while (l<=n&&a[l].position==a[l-1].position){
				Delete(l);++l;
			}//Delete all the beads in the same position.
		}
		else{
			++r;if (r>n) break;Insert(r);
//			不符题意，只能加入更多的珠子 
			while (a[r].position==a[r+1].position){
				r++;if (r>n) break;Insert(r);
			}//Insert all the beads in the same position.
		}
	}
	printf("%d",ans);
	return 0;
}

---

$$洛谷P5022旅行$$

$【题意】：$




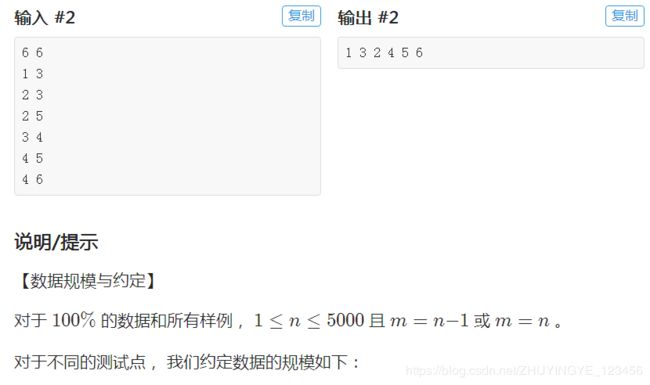
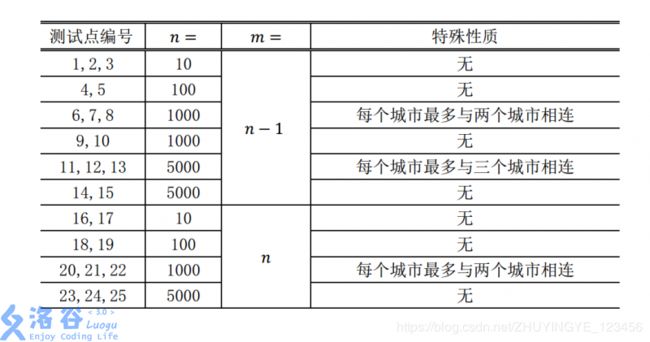
$【思路】：$ 首先，拿到这么一道竞赛题目，我们先看题意（废话），然后我们应该看看题目的数据范围。

我们发现前$60\%$的数据是一棵$树$，而后$40\%$的数据是一棵$基环树$（即一颗树加上一条边）。

我们先来看看一棵树的情况：很简单，只需从$1$开始，每次遍历最小的点即可。直接上代码（代码中的边已经排好序）。

namespace case_one{
	int cnt=0;bool vis[5100];
	inline void dfs(int u){
		ans[++cnt]=u;vis[u]=true;
		for(int i=h[u];i;i=e[i].next){
			register int to=e[i].to;
			if (!vis[to]) dfs(to);
		}
	}
	void simulation_main(){
		memset(vis,0,sizeof(vis));dfs(1);
		for(int i=1;i<=n;i++)
			printf("%d ",ans[i]);
	}
}

好的，$60$分到手。

对于基环树的情况，因为$N,M$不是很大，所以$O(N^2)$或$O(N\times M)$的方法可以通过此题。

因为只有一条边是我们遍历不到的，所以我们可以枚举我们删除哪条边，然后接下来就是一棵树的情况了。

当然这样可能会$TLE$，那这么办？

我们可以考虑剪枝，今天而言，就是如果当前的答案一定不会更优时，就可以返回进行下一次搜索了。

具体的看代码（一样，边已经排好序了）：

namespace case_two{
	int cnt=0,res[5100],du,dv;
	bool vis[5100],flag;
	inline bool check(int u,int v){
		if (u==du&&v==dv)
			return false;
		if (u==dv&&v==du)
			return false;
		return true;
	}
	void dfs(int u){
		if (u<ans[cnt]) flag=true;
		if (flag) res[cnt++]=u;
		else if (u>ans[cnt]){
			/*cnt--;*/return;
		}
		else cnt++;vis[u]=true;
		for(int i=h[u];i;i=e[i].next){
			register int to=e[i].to;
			if (!vis[to]&&check(u,to)) dfs(to);
		}
	}
	void simulation_main(){
		memset(ans,127,sizeof(ans));
		for(int i=1;i<=m;i++){
//			memset(res,0,sizeof(res));
			memset(vis,0,sizeof(vis));
			du=b[i].from;dv=b[i].to;
			cnt=0;flag=false;dfs(1);
			if (cnt==n) memcpy(ans,res,sizeof(res));
		}
		for(int i=0;i<n;i++)
			printf("%d ",ans[i]);
	}
}

最后讲讲如何把边排序。如果大家用vector的话，那很简单。但是众所周知，STL很慢，这题用vector就很可能$TLE$（当然，不是一定，还得看看人品运气）。

所以我们只能用$链式前向星$解决。其实我们只需要把所有的边按边权$从大到小$排序（为什么要从大到小，因为链式前向星加入边后，遍历时会反过来，所以从大到小插入，就代表从小到大访问），然后依次加入即可。具体看代码：

int main(){
//	freopen("t1.in","r",stdin);
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;i++){
		scanf("%d",&a[i].from);
		scanf("%d",&a[i].to);
		a[i+m].from=a[i].to;
		a[i+m].to=a[i].from;
		b[i].from=a[i].from;
		b[i].to=a[i].to;
	}
	sort(a+1,a+2*m+1);
	for(int i=1;i<=2*m;i++)
		add(a[i].from,a[i].to);
}

然后就是整题的代码了……

$【代码】：$

int n,m,ans[5100];
struct edge{
	int from,to;
	bool operator < (edge c) const{
		return to>c.to;
	}
}a[10100],b[5100];
struct node{
	int next,to;
}e[10100];int h[5100],tot;
inline void add(int a,int b){
	e[++tot]=(node){h[a],b};h[a]=tot;
//	e[++tot]=(node){h[b],a};h[b]=tot;
}
namespace case_one{
	int cnt=0;bool vis[5100];
	inline void dfs(int u){
		ans[++cnt]=u;vis[u]=true;
		for(int i=h[u];i;i=e[i].next){
			register int to=e[i].to;
			if (!vis[to]) dfs(to);
		}
	}
	void simulation_main(){
		memset(vis,0,sizeof(vis));dfs(1);
		for(int i=1;i<=n;i++)
			printf("%d ",ans[i]);
	}
}
namespace case_two{
	int cnt=0,res[5100],du,dv;
	bool vis[5100],flag;
	inline bool check(int u,int v){
		if (u==du&&v==dv)
			return false;
		if (u==dv&&v==du)
			return false;
		return true;
	}
	void dfs(int u){
		if (u<ans[cnt]) flag=true;
		if (flag) res[cnt++]=u;
		else if (u>ans[cnt]){
			/*cnt--;*/return;
		}
		else cnt++;vis[u]=true;
		for(int i=h[u];i;i=e[i].next){
			register int to=e[i].to;
			if (!vis[to]&&check(u,to)) dfs(to);
		}
	}
	void simulation_main(){
		memset(ans,127,sizeof(ans));
		for(int i=1;i<=m;i++){
//			memset(res,0,sizeof(res));
			memset(vis,0,sizeof(vis));
			du=b[i].from;dv=b[i].to;
			cnt=0;flag=false;dfs(1);
			if (cnt==n) memcpy(ans,res,sizeof(res));
		}
		for(int i=0;i<n;i++)
			printf("%d ",ans[i]);
	}
}
int main(){
//	freopen("t1.in","r",stdin);
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;i++){
		scanf("%d",&a[i].from);
		scanf("%d",&a[i].to);
		a[i+m].from=a[i].to;
		a[i+m].to=a[i].from;
		b[i].from=a[i].from;
		b[i].to=a[i].to;
	}
	sort(a+1,a+2*m+1);
	for(int i=1;i<=2*m;i++)
		add(a[i].from,a[i].to);
//	for(int i=1;i<=n;i++)
//		for(int j=h[i];j;j=e[j].next)
//			printf("An edge from %d to %d\n",i,e[j].to);
	if (m==n-1) case_one::simulation_main();
	else case_two::simulation_main();
	return 0;
}