21869 Problem C 货币系统 （顺便进行01背包的总结归纳，内含自己想的有趣例子帮助理解。。）

问题 C: 货币系统

时间限制: 1 Sec  内存限制: 128 MB
提交: 94  解决: 32
 

题目描述

母牛们不但创建了他们自己的政府而且选择了建立了自己的货币系统。
[In their own rebellious way],，他们对货币的数值感到好奇。
传统地，一个货币系统是由1,5,10,20 或 25,50, 和 100的单位面值组成的。
母牛想知道有多少种不同的方法来用货币系统中的货币来构造一个确定的数值。
举例来说, 使用一个货币系统 {1,2,5,10,...}产生 18单位面值的一些可能的方法是:18x1, 9x2, 8x2+2x1, 3x5+2+1,等等其它。
写一个程序来计算有多少种方法用给定的货币系统来构造一定数量的面值。
保证总数将会适合long long (C/C++) 和 Int64 (Free Pascal)。

输入

输入包含多组测试数据

 

货币系统中货币的种类数目是 V 。 (1<= V<=25)
要构造的数量钱是 N 。 (1<= N<=10,000)

第 1 行:	二整数， V 和 N
第 2 ..V+1行：	可用的货币 V 个整数　(每行一个　每行没有其它的数)。

 

输出

单独的一行包含那个可能的构造的方案数。

样例输入

3 10
1 2 5

样例输出

10

经验总结

本题是完全背包问题，将每种货币的面值看作是物品的价值，将要构造的目标钱数看作是背包总大小，求的可能的构造方法数即为求使背包恰好装满可能的方案数。这里，状态转移方程是dp [ i ] [ v ] = dp [ i - 1 ] [ v ] + dp [ i - 1 ] [ v-v[ i ] ] ，dp[ i ] [ v ] 代表当前能构造出 钱数v的方案数，初始化时 dp[ 0 ] =1 ，其余均为 0 。最后提醒一下，dp数组要用长整型定义。。。

0-1 背包问题：

这里，还是自我稍微总结一下背包问题的理解，可能是自己的智商捉急。。《算法笔记》上的背包问题的描述不是怎么看的懂。。网上搜了一下别的大佬写的博客，在此自己总结一番。

给定 n 种物品和一个容量为 C 的背包，物品 i 的重量是 wi，其价值为 vi 。如何选择装入背包的物品，使得装入背包中的物品的总价值最大？

思路：建立dp [ i ] [ v ]  的二维数组，( 0 < = i < = n ,  0 < = v < = V )   一定要搞清楚 dp [ i ][ v ] 的含义，它表示 在对第 i 件物品进行过取舍操作（选择放入，或者选择不放）之后，大小为v的背包所能获得的最大价值 ，这个一定要理解清楚，说一下这里可能将 v 理解为当前背包内物品的体积之和，这个 很明显有些地方说不通，比如刚开始什么都没放，v如果为体积之和，就应该为 0 那么dp [ ] [ 1 ~ V ]就无法解释了。
还有一点，就是，一定要理解，多阶段动态规划问题，它可以描述成若干个有序的阶段，且每个状态只与上一个状态有关！因此，我们要知道在对于第 i 件物品进行操作时（还没进行操作），此时的dp [ i-1 ] [  ]数组中已经存储的是在对前 i - 1 件物品进行完操作之后，背包大小为 0 - V 的所有背包所能获得的最大价值。因此，对第 i 件物品 进行操作时 ， 只需要看dp [ i - 1 ] [ ] 数组就可以了。

怎么理解dp [ i ] [ ] 存放的就一定是当前背包可以获得的最大价值呢？举一个形象的例子吧。。。（此例为本人原创，可以帮助理解，禁止抄袭。。转载请注明出处= =）

设定：

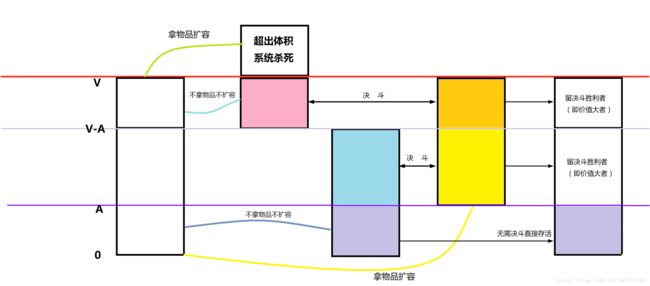
当前，有V+1个人排成一队，他们每个人身上都背着一个背包，第一个人的背包大小为0 ，后面每个人都比前一个人的背包大  1，最后一个人的背包大小为V，他们的背包有一个特性，就是可以变大。这些人也有一个特异功能，为了获取最大价值，在做选择的时候，他们可以影分身成两个人（当然背包大小也完全复制了），一个人选择拿，一个人选择不拿。之后这两个人就独立存在，并且再次遇到选择时仍可以进行影分身。刚开始，他们的包里啥都没有，所以价值均为0。 

规则：

1. 相同背包大小的人只能存在一个，即如果出现两个背包大小相同的人，他们就要进行决斗，谁的背包内的物品价值大，谁就能赢得最终的胜利，失败者被杀死。
          2 . 如果背包扩容超过了V，那么系统认定这个人太贪心了，直接杀死，毫不留情，木的感情(“▔□▔)。
          3.  他们每个人都分别站到一个传送带面前，所有的传送带都会送来同一件物品，但每次送来的物品大小和价值都不同
          4.  这些人对每件物品都要进行选择，即都要进行影分身，一个人扩容背包拿走物品，另一个人不拿物品也无需扩容背包，在做完选择后，背包大小相同的人必须进行一次决斗。

分析：

比如，第 i 次传送带送来一个体积为 A 价值为 B 的物品，其实要分析的人可以划分为两类

          1.  背包大小为V-A+1 到 V 的人，他们选择拿下物品的影分身被系统给干掉了。。他们只留下了没有拿这个物品的影分身。
          2.  背包大小为0 到 V-A的人，他们的两个影分身都没有被系统杀死，这两部分人都有可能会决斗，（如果A=V/2，那么不拿物品的那部分人不需要进行决斗）

规则表示图如下。。。希望能有助于理解。。

这样当传送带传送完n个物品之后，实际上已经进行了n次决斗，留下的都是最强的，即当背包容量为v时的最大价值~~(●´∀｀●)
这里，遍历dp数组需要从后往前遍历，因为后面的确定好就不会再被更改了，如果从前往后遍历就是完全背包问题了~这个想一下就能理解啦~

 

正确代码

#include 
#include 
#include 
using namespace std;
const int maxv=10010,maxn=30;
long long dp[maxv],v[maxn];

int main()
{
	int n,N;
	while(~scanf("%d %d",&n,&N))
	{
		for(int i=1;i<=n;++i)
		{
			scanf("%lld",&v[i]);
		}
		for(int i=0;i<=N;++i)
		{
			dp[i]=0;
		}
		dp[0]=1;
		int num=0;
		for(int i=1;i<=n;++i)
		{
			for(int x=v[i];x<=N;++x)
			{
				dp[x]+=dp[x-v[i]];
			}
		}
		printf("%lld\n",dp[N]);
	}
    return 0;
}