Java尚硅谷基础笔记-day4数组-数组常见算法
第三章 数组
- 3.4 数组中涉及的常见算法
3.1 数组的概述
3.2 一维数组的使用
3.3 多维数组的使用
3.4 数组中涉及的常见算法
3.5 数组工具类的使用
3.6 数组使用中的常见异常
3.4 数组中涉及的常见算法
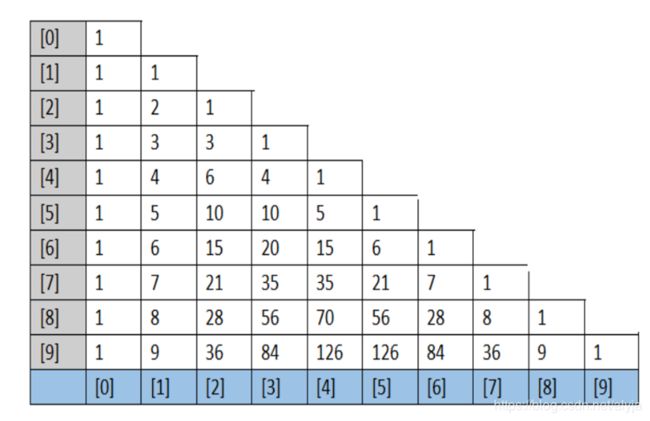
练习1:杨辉三角
使用二维数组打印一个 10 行杨辉三角
【提示】
- 第一行有 1 个元素, 第 n 行有 n 个元素
- 每一行的第一个元素和最后一个元素都是 1
- 从第三行开始, 对于非第一个元素和最后一个元素的元素。即:
yanghui[i][j] = yanghui[i-1][j-1] + yanghui[i-1][j];
public class arrayTest {
public static void main(String[] args) {
int[][] yanghui=new int[10][];
for(int i=0;i<yanghui.length;i++) {
yanghui[i]=new int[i+1];
yanghui[i][0]=1;
yanghui[i][i]=1;
for(int j=1;j<yanghui[i].length-1;j++) {
yanghui[i][j]=yanghui[i-1][j]+yanghui[i-1][j-1];
}
}
for(int i=0;i<yanghui.length;i++) {
for(int j=0;j<yanghui[i].length;j++) {
System.out.print(yanghui[i][j]+" ");//不换行输出
}
System.out.println( );
}
}
}
练习二:回形数
 {
Scanner scanner = new Scanner(System.in);
System.out.println("输入一个数字");
int len = scanner.nextInt();
int[][] arr = new int[len][len];
int maxX=arr.length-1;
int maxY=arr.length-1;
int minX=0;
int minY=0;
int count=1;
while(minX<maxX) {
for(int x=minX;x<=maxX;x++) {
arr[minY][x]=count++;
}
minY++;
for(int y=minY;y<=maxY;y++) {
arr[y][maxX]=count++;
}
maxX--;
for(int x=maxX;x>=minX;x--) {
arr[maxY][x]=count++;
}
maxY--;
for(int y=maxY;y>=minY;y--) {
arr[y][minX]=count++;
}
minX++;
}
// 遍历
for (int m = 0; m < arr.length; m++) {
for (int n = 0; n < arr[m].length; n++) {
System.out.print(arr[m][n] + "\t");
}
System.out.println();
}
}
}
3.4.2 数组元素得最大值,最小值,平均值和总和
练习1:定义一个int型的一维数组,包含10个元素,分别赋一些随机整数,
然后求出所有元素的最大值, 最小值,和值, 平均值, 并输出出来。
要求: 所有随机数都是两位数。
int[]arr=new int[10];
for(int i=0;i<arr.length;i++) {
arr[i]=(int)(Math.random()*90+10);
}
for(int i=0;i<arr.length;i++) {
System.out.println(arr[i]);
}
int max=arr[0];
int min=arr[0];
int sum=0;
for(int i=0;i<arr.length;i++) {
sum+=arr[i];
if(arr[i]>max) {
max=arr[i];
}
if(arr[i]<max) {
max=arr[i];
}
}
double avg=sum/arr.length;
System.out.println(max);
System.out.println(min);
System.out.println(sum);
System.out.println(avg);
3.4.3 数组的复制,反转和查找
数组的复制
//1.错误的复制 arr1=arr2 赋值
int[]arr1=new int[] {1,2,3,4,5,6};
int[]arr2=new int[6];
for(int i=0;i<arr1.length;i++) {
System.out.print(arr1[i]+"\t");
}
System.out.println( );
arr2=arr1;
for(int i=0;i<arr2.length;i++) {
if (i%2==0) {
arr2[i]=0;
}
}
for(int i=0;i<arr1.length;i++) {
System.out.print(arr1[i]+"\t");
}
//输出:1 2 3 4 5 6
//输出:0 2 0 4 0 6
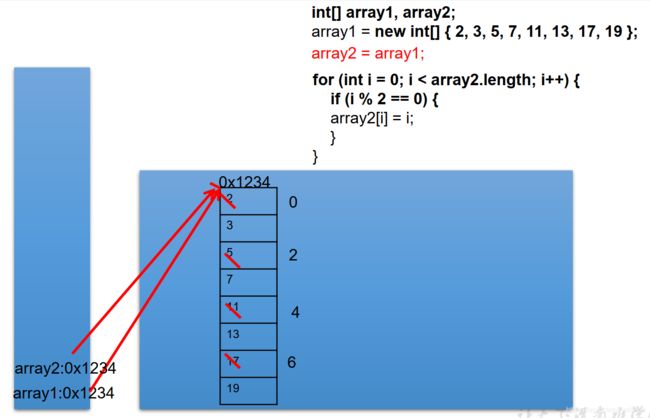
//改变arr2值,可以改变arr1,这是因为arr2和arr1指向同一个地址
将arr1保存的数组地址值赋给了arr2,使得arr1和arr2共同指向堆空间中的同一个数组实体
//数组的复制
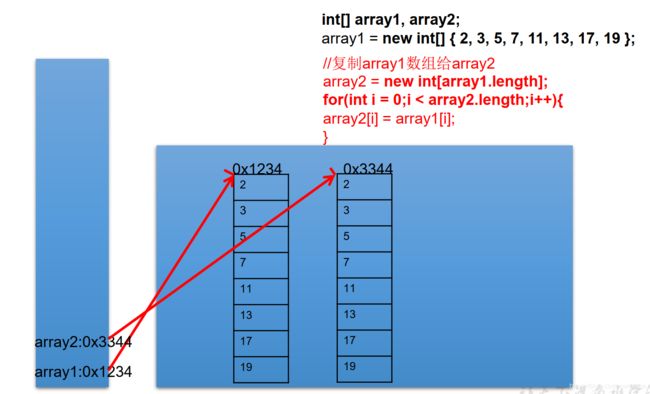
int[] arr1, arr2;
arr1 = new int[] { 2, 3, 5, 7, 11, 13, 17, 19 };
//复制array1数组给array2
arr2 = new int[arr1.length];
for(int i=0;i<arr2.length;i++) {
arr2[i]=arr1[i];
}
通过new的方式,给arr2在堆空间中新开辟了数组的空间。将arr1数组中的元素一个一个赋值到arr2数组中
数组的反转
//方法一
String[]arr1=new String[] {"aa","bb","cc","nn","vv","xx","zz"};
for(int i=0;i<arr1.length/2;i++) {
String temp=arr1[i];
arr1[i]=arr1[arr1.length-1-i];
arr1[arr1.length-1-i]=temp;
}
for(int i=0;i<arr1.length;i++) {
System.out.print(arr1[i]+"\t");
}
//方法二:
String[]arr1=new String[] {"aa","bb","cc","nn","vv","xx","zz"};
for(int i=0,j=arr1.length-1;i<j;i++,j--) {
String temp=arr1[i];
arr1[i]=arr1[j];
arr1[j]=temp;
}
数组的查找
线性查找
方式一
//线性查找
String[]arr1=new String[] {"aa","bb","cc","nn","vv","xx","zz"};
String dest="bb";
boolean isFlag=true;
for(int i=0;i<arr1.length;i++) {
if(arr1[i].equals(dest)) {
System.out.print("找到了指定元素,位置为:"+i);
isFlag=false;
break;
}
}
if(isFlag) {
System.out.print("没有找到");
}
方式二
//线性查找
String[]arr1=new String[] {"aa","bb","cc","nn","vv","xx","zz"};
String dest="bb";
int i;
for(int i=0;i<arr1.length;i++) {
if(arr1[i].equals(dest)) {
System.out.print("找到了指定元素,位置为:"+i);
break;
}
}
if(i==arr1.length) {
System.out.print("没有找到");
}
二分法:判断区间依次减半
前提:数组有序
int[]arr1=new int[] {-2,4,8,23,35,45,55,67,87,98};
int dest=55;
boolean isFlag=true;
int start=0;
int end=arr1.length-1;
while(start<=end) {
int mid=(start+end)/2;
if(dest==arr1[mid]) {
System.out.print("找到了指定元素,位置为:"+mid);
isFlag=false;
break;
}else if(dest<arr1[mid]) {
end=mid-1;
}else {
start=mid+1;
}
}
if(isFlag) {
System.out.print("没有找到");
}
3.4.4 数组的排序
排序算法
衡量排序算法的优劣:1.时间复杂度2.空间复杂度 3.稳定性
十大排序算法:
选择排序:直接选择排序,堆排序
交换排序:冒泡排序,快速排序
插入排序:直接插入排序,折半插入排序,Shell排序
归并排序
桶式排序
基数排序
冒泡排序
时间复杂度: O(n^2)
排序思想:
- 比较相邻的元素。如果第一个比第二个大(升序),就交换他们两个。
- 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。这步
做完后,最后的元素会是最大的数。 - 针对所有的元素重复以上的步骤,除了最后一个。
- 持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要
比较为止。
int[]arr1=new int[] {-2,56,8,2,35,30,55,67,124,98};
for(int i=1;i<arr1.length-1;i++) {
for(int j=0;j<arr1.length-i;j++) {
if(arr1[j]>arr1[j+1]) {
int temp=arr1[j];
arr1[j]=arr1[j+1];
arr1[j+1]=temp;
}
}
}
for(int i=0;i<arr1.length;i++) {
System.out.print(arr1[i]+"\t");
}
快速排序
时间复杂度: O(nlogn)
排序思想:
- 从数列中挑出一个元素,称为"基准"(pivot),
- 重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准
值大的摆在基准的后面(相同的数可以到任一边)。在这个分区结束之后,
该基准就处于数列的中间位置。这个称为分区(partition)操作。 - 递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数
列排序。 - 递归的最底部情形,是数列的大小是零或一,也就是永远都已经被排序好
了。虽然一直递归下去,但是这个算法总会结束,因为在每次的迭代
(iteration)中,它至少会把一个元素摆到它最后的位置去。
public class arrayTest {
public static void main(String[] args) {
int[]arr1=new int[] {20,80,14,-2,56,8,2,35,20,30,10,67};
int low=0;
int high=arr1.length-1;
Quick_short(arr1,low,high);
for(int i=0;i<arr1.length;i++) {
System.out.print(arr1[i]+"\t");
}
}
//进行分区,大于arr[pivot]的在右边,小于其的在左边
public static int partition(int[] arr, int low, int high) {
int pivot=low;
int temp=arr[pivot];
while(low<high) {
while(low<high&&arr[high]>temp) {//如果右边的值一直比temp大,则high一直往中间推。当<=时,暂停
high--;}
//暂停之后将值赋给arr[low],开始从左边继续看
if(low<high) {arr[low]=arr[high];low++;}
while(low<high&&arr[low]<temp) {//如果左边的值一直比temp小,则low一直往中间推。当>=时,暂停
low++;
}
//暂停之后将值赋给arr[high],开始从右边继续看
if(low<high) {arr[high]=arr[low];high--;}
}
//退出循环:low=high,交换low所在位置和pivot的值,并且返回此时low的值
arr[low]=temp;
return low;//返回arr[pivot]所在位置
}
//递归过程
public static int[] Quick_short(int[] arr,int s,int t) {
if(s<t) {
int i=partition(arr,s,t);
Quick_short(arr,i+1,t);
Quick_short(arr,s,i-1);
}
return arr;
}
}
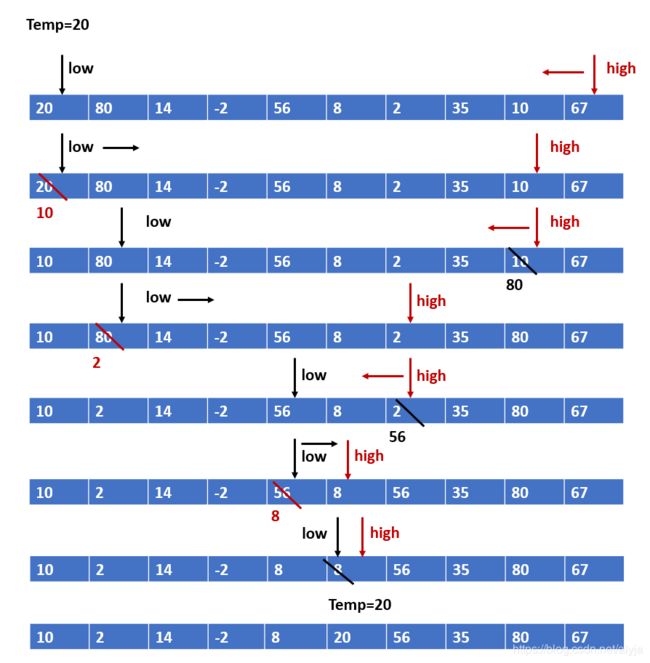
分区部分的图解过程:
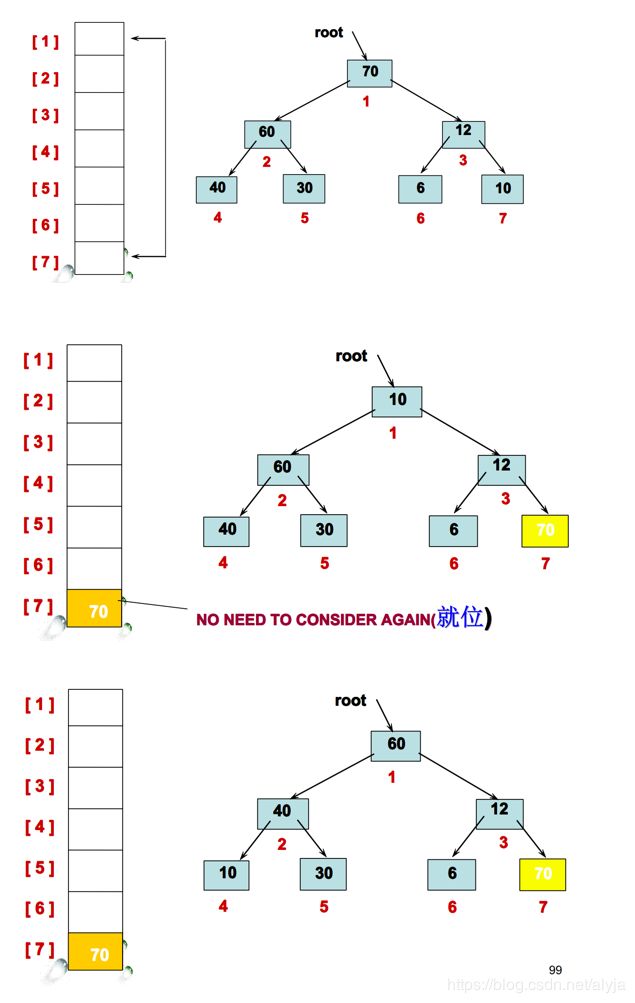
堆排序
堆排序(Heapsort) 是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。(大于或等于:大顶堆,小于或等于:小顶堆)
算法描述(大顶堆):
int arr=new int[]{30,60,8,40,70,12,10}
步骤1:将初始待排序关键字序列(R1,R2….Rn)构建成大顶堆,此堆为初始的无序区;
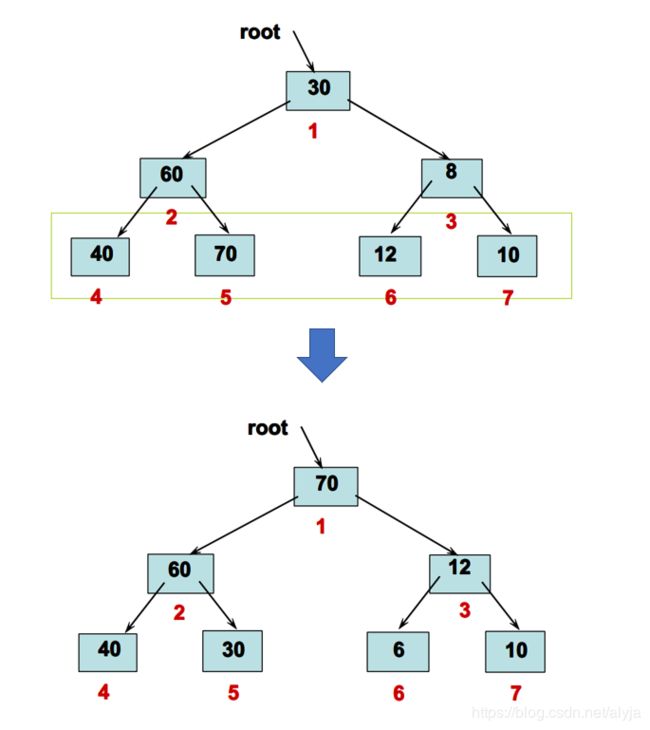
步骤2:将堆顶元素R[1]与最后一个元素R[n]交换,此时得到新的无序区(R1,R2,……Rn-1)和新的有序区(Rn),且满足R[1,2…n-1]<=R[n];
步骤3:无序区(R1,R2,……Rn-1)重新建堆。然后再次将R[1]与Rn-1交换,再将(R1,R2….Rn-2)重新建堆。不断重复此过程,直到重新建堆元素为一个。
归并排序
将已有序的子序列合并,得到完全有序的序列;即先使用每个子序列有序,再使得子序列段间有序。若将两个有序表合并成一个有序表,称为2-路归并。
算法描述:
步骤1:把长度为n的输入序列分成两个长度为n/2的子序列;
步骤2:对这两个子序列分别采用归并排序;
步骤3:将两个排序好的子序列合并成一个最终的排序序列。