Analysis On Tic-Tac-Toe

It's a long time that I haven't written any page. Because I've got many things to do these days, even on weekends I have to spare much time to prepare for my tutoring. However, I never stop thinking about the program which teacher had asked us to implement.

And that is " Tic-Tac-Toe ".
" Tic-Tac-Toe " is a relatively harder problem with recursion to a beginner like me. After reading some helpful and articulate articles on the web, I finally get some ideas about that. And, here in my blog, I'm willing to share them with you, my buddies. So, here they are.

Fist, let's spent a little time to have a rough observation on "Tic-Tac-Toe", which is also called as "Noughts and Crosses".The simple rules are that:
1). it's chess board is a 3 * 3 .
2). once you occupied a position, you and your adversary can't remove or "eat" it.

3).the first one who make a straight three positions a line on the row or column or diagonal will be the winner.

As we all know, write such aprogram for "man against man" is simple. The key to this game is that how to make a computer to play like a wised guy. And this is something about the AI ( Artificial Intelegence ).

To make a computer have intellegence ,we have to make it can "preview" further steps. So we have to recursively pre-calculate all the possibilities. But as we all know, to get all possibilities calculated beforehand costs much, and it's a algorithm beyond feasibility. So, we have no choice but to figure out some better algorithms to replace it.

Here comes the MiniMax algorithm and Alpha-Beta algorithm.

MiniMax:

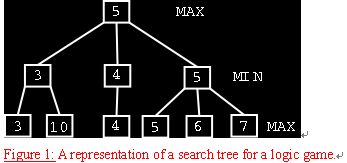
The Min-Max algorithm is applied in two player games, such as tic-tac-toe, checkers, chess, go, and so on. All these games have at least one thing in common, they are logic games. This means that they can be described by a set of rules and premisses. With them, we can deduce the next availabe move from the current condition. So, to make it easier to understand, we suppose that there are two players involved, MAX and MIN. A search tree is generated, depth-first, starting with the current game position upto the end. Then, the final game position is evaluated from MAX’s point of view, as shown in Figure 1. Afterwards, the inner node values of the tree are filled bottom-up with the evaluated values. The nodes that stands for the MAX player receive the maximum value of it’s children while the nodes for the MIN player will select the minimum value of it’s children. Here, you may be wondering what does the value or the number in the box illustrated in the Figure 1. mean. Let me tell you, it quantifies the likehood how the move ( taking the position which the box stands for ) is going to make the player to win. More simply, the value represents that how good the move is. So, by receive the maximum value of it's children, the MAX can is always on the most likely road to win. Vice versa.

Alpha-Beta:
This algorithm is a optimization or a mend or improvement on the MiniMax. It can save many insiginficant calculations , thus it make the MiniMax algorithm more recievable and fast. Then how does Alpha-Beta make this ?
At first, you must have a base idea that only in very simple game can we generate it's entire search tree ( take all the possibilites into account )  in a short time. So, instead of knowing the full path that leads to victory, the decisions are made with the path that might lead to victory. This is , we choose the relatively more likely by just looking at some trees.
There are two ways to make this ides come true.

One way is to limit the depths of the game ( search ) tree. That's like that a man who see 10 steps further is relatively equal to us when compare him to a man who can see 11 steps further. By reducing the accuracy , we win enormous time and space.

The other way is using Alpha-Beta algorithm, which you can also call it a tree-cutoff algorithm here. The detail thoughts are that: use a function that evaluates the current game position from the point of view of some player. It does this by giving a value to the current state of the game, like counting the number of pieces in the board, for example. Or the number of moves left to the end of the game, or anything else that we might use to give a value to the game position.Instead of evaluating the current game position, the function might calculate how the current game position might help ending the game.This function will have to take into account some heuristics. Heuristics are knowledge that we have about the game, and it can help generate better evaluation functions.
To make this algorithm more clear , I give Figure 2. and a pseudo code.

1. Have two values passed around the tree nodes:
2. At MAX level, before evaluating each child path, compare the returned value with of the previous path with the beta value. If the value is greater than it abort the search for the current node. Do the same thing to MIN level at the same time.

Pseudocode Here:

Here, when we care our Tic-Tac-Toe only , which is a "zero-sum" game, we can use only one fuction to evaluate. It's easy to understand that if the move is favorable to MAX, then it must be unfavorable to MIN. So, we have to simple take the nega value when considered to MIN. Isn't it ?

Concerned about the limited space here , I 'll paste the code ( which is done by Bao Yu, my lovely teacher ) on my next blog.

Let's get ready to it.