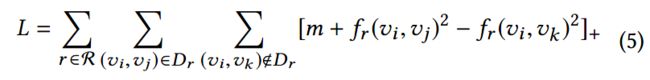【论文解读 KDD 2018 | PME】PME: Projected Metric Embedding on Heterogeneous Networks for Link Prediction

论文链接：http://net.pku.edu.cn/daim/hongzhi.yin/papers/KDD18-Hongxu.pdf

代码链接：https://sites.google.com/view/hongxuchen

会议：KDD 2018

---

目录

1 摘要

1.1 挑战

1.2 为解决上述挑战，作者提出

2 介绍

2.1 现有的方法

2.2 动机

2.3 启发

2.4 作者提出

2.4.1 PME

2.4.2 loss感知的自适应采样方法

2.5 贡献

3 PROJECTED METRIC EMBEDDING (PME)

3.1 定义及问题

3.2 The PME Model and Optimization

3.3 Bidirectional Negative Sampling Strategy

3.4 Loss-aware Adaptive Positive Sampling Strategy

4 实验

5 总结

---

1 摘要

本文研究的是异质信息网络的embedding问题。

1.1 挑战

（1）现有的大多数方法都是采用点乘的方式衡量节点在低维空间的相似度，然而这种方法只能保留一阶相似度，不足以捕获网络的全局结构信息。

（2）和同质信息网络相比，异质信息网络中边的种类多样，也就是关系有多种，所以边的分布是非常不均匀的（歪斜的）。比如有一些类型的边可能占据了所有边数的大部分，而有一些类型的边在图中只占据很少的一部分。采样会带来边的分布不均衡的问题。

1.2 为解决上述挑战，作者提出

（1）PME模型，基于度量学习（metric learning）来捕获一阶和二阶的相似性。

（2）为了缓解先用的度量学习方法在几何上的不灵活性，作者分别在节点空间和关系空间构建节点和关系的embedding，而不是将节点和关系的embedding映射到同一空间中。【这点和HEER很像，都是KDD 2018】

（3）为了学习到embeding，首先将节点从节点空间映射到相应的关系空间中，然后计算投影节点之间的相似度。

（4）为了解决给定关系下的边分布的歪斜问题，并且避免每个关系的过采样和欠采样，作者提出了loss感知的自适应采样方法用于模型的优化。

2 介绍

和同质网络嵌入相比，HIN中节点之间的相似性不仅仅衡量了距离，还具有语义信息。

2.1 现有的方法

为了建模有特定语义信息的边，有学者提出了基于元路径的方法，还有人提出使用embedding矩阵衡量不同类型的节点间相似度。但是这些方法都使用点乘来衡量节点向量间的相似度。

2.2 动机

点积不是一个基于距离学习的度量，因为它不满足三角不等式的条件，而三角不等式是泛化一个学习度量的关键。三角不等式是指：对于任意三个节点，两对节点间的距离和应大于剩余的那对节点间距离。

例如，节点a、b都和c距离近，通过三角不等式发现a和b也距离近。然而基于点积的相似度计算方法只能根据现有的边捕获到局部结构信息，即一阶相似度（a、b都和c距离近），但不能捕获到二阶相似度（a和b距离也近）。因为后者取决于节点共享的邻域结构。众所周知，一阶相似度是不足以保留网络的全局结构信息的。

2.3 启发

基于知识图谱（KG）的表示学习和本文工作相关。Trans-family models（TransE、TransH、TrasnR）可以有效的对知识建模。本文工作中位不同类型的关系建立不同的投影矩阵，就是受TransR的启发。但是两者设计的目的不同，本文工作的目的是缓解度量学习中的几何上的不灵活性问题（geometric inflexibility）。

2.4 作者提出

2.4.1 PME

PME模型（Projected Metric Embedding），基于度量或是距离学习，用简洁的方式同时保留一阶和二阶相似性。

如果直接采用欧氏距离作为度量的话，每对相连的节点会趋向于同一点，而且当数据集大的时候，节点的所有邻居都会趋于同一点。（intrinsic geometric inflexibility）

为了解决上述问题，PME模型引入了一个针对特定关系的投影嵌入矩阵，从而实现在不同空间对节点和边进行建模。并且使用欧氏距离在相应的关系空间进行相似度计算。从而实现一些节点在节点空间可能距离很远，但是在相应的关系空间距离很近。

图1

PME的基本思想如图1所示，对于每条边，首先使用矩阵将节点从object space映射到r-relation space。这种针对特定关系的映射可以使得有连边的节点在空间中距离近，没有连边的距离远。

由于HIN中有许多观察不到的连边，所以采用了双向的popularity-biased的负采样方法来优化PME模型。

2.4.2 loss感知的自适应采样方法

边的分布是非常不均匀的（歪斜的）。比如有一些类型的边可能占据了所有边数的大部分，而有一些类型的边在图中只占据很少的一部分。均匀采样会带来边的分布不均衡问题，带来信息损失。

为了解决多种类型的边联合训练的问题，Tang等人提出的PTE模型中采用了对每个类型的边进行交替采样的方法。首先均匀采样一种关系类型，然后在图中随机采样一个属于此类型的边，这样每种关系类型都有相同数量的边作为训练数据。但是这会导致数量少的那种类型的边被过采样，数量多的类型的边被欠采样。而且在每种类型的关系中，保留节点对间的相似度的难度不同，在训练过程中，这个难度还是随着模型参数的更新而动态变化的。因此对于不同类型的关系，所需的训练数据也应该不同。

为了解决异质边分布的偏斜问题，作者提出了loss感知的自适应采样方法，为模型优化获取训练数据。基本思想是，loss大的关系类型应该有更高的概率被采样，因为他们需要更多的训练数据来纠正现有的模型参数。

2.5 贡献

（1）提出PME模型，适用于任意HIN的嵌入学习。学习到了一个距离度量同时保留一阶和二阶相似性，为节点和边分别引入不同的空间从而避免了现有度量方法的缺点，并且易于向大型网络扩展。

（2）为了解决异质边分布的偏斜问题，提出了loss感知的自适应采样方法获取训练数据。

（3）在Yelp数据集上进行了预测任务和可扩展性的实验，和state-of-the-art相比体现了PME的优越性。

3 PROJECTED METRIC EMBEDDING (PME)

3.1 定义及问题

定义

• HIN定义为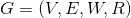，V是节点集合，E是边集合，R是边类型集合，W是每条边的权重组成的集合。
• 边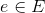可定义为。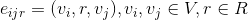

问题

给定一个异质信息网络G，输出

（1）节点的低维向量表示，第i行是节点的向量表示。

（2）关系的低维潜在表示，是特定关系的投影矩阵的维度。第r片（slice）是关系r的投影矩阵。

3.2 The PME Model and Optimization

首先将节点的表示映射到特定关系的投影矩阵，投影后的向量表示定义如下：

计算两个相连节点的相似度，节点和由类型为r的边相连，两节点在r-relation space的距离计算如下：

使用欧氏距离计算，是因为它既满足了三角不等式，又保留了一阶和二阶相似性。考虑到带有权重的边，对被观察的边的评分函数定义如下：

作者的目标是让有连边的节点在特定的关系空间中距离相近，而没有连边的节点距离相远。基于margin的目标函数定义如下，其中m>0是safety margin的大小，。

学习HIN的嵌入表示问题就转换成最小化下面的目标函数问题：

3.3 Bidirectional Negative Sampling Strategy

直接最小化（6）式需要很大的计算量，因为网络中观察不到的边的数量是可观察到的节点数和边数的立方。受负采样技术的启发，作者不在采样所有的观察不到的样本，而是选取一些最有可能是负样本的样本以优化模型。

传统的负采样技术仅仅固定节点对中的一个节点和关系，负采样连边另一端的节点。比如对于无向边，固定和r，生成负样本。这种方法可用于同质信息网络，若直接应用于HIN，则会影响模型的效果。

所以，作者从一条边的两端分别进行负采样。对于一个正样本，先固定和r，生成K个负样本；然后固定和r，生成K个负样本。综上，目标函数重新定义为：

3.4 Loss-aware Adaptive Positive Sampling Strategy

由于HIN包含许多根据链路类型抽取出来的子网络，而且正样本的分布是不均衡的，所以正样本的获取也是一项挑战。若均匀采样的话，就学习不到规模小的子网络的结构信息。为了让模型更通用，作者提出自适应的采样正样本的方法。

监控每个子网络的loss，若某个特定的子网络的loss相对其他子网络大，则自适应地在下一个epoch中增加这种类型的边的正样本。反之，在下一个epoch中减少这种类型的正样本。

设表示每个子网络的loss组成的序列，在每次训练后计算每个loss的占比。显然这个正样本采样器会随着模型参数的变化而变化，因为模型参数的变化会带来每个子网络loss的变化，也就是说这个采样器是自适应的。由于刚开始训练时每个子网络的loss都是0，所以根据子网络的原始边分布，初始化每个边的正采样概率。

PMF的优化算法如下：

4 实验

数据集：Yelp

两个实验任务：

（1）评估预测准确性：对于正样本，选取5000个负样本，通过式（2）计算欧氏距离。然后根据这5001个样本对vi的距离，对其排序。选取top-k和样本，若，则预测成功，否则不成功。

（2）链接二分类：预测给定的链接是否存在于网络中。

对比方法：

在两个任务上效果均好于metapath2vec、node2vec、PTE、EOE。

5 总结

提出PME模型解决HIN的嵌入学习问题，使用relation-specific spaces对异质的节点和边进行了建模。

使用欧氏距离作为节点间相似度的度量，既满足了三角不等式，又同时保留了一阶和二阶相似性。

为了优化PME模型，引入loss感知的自适应正采样机制，克服了异质边分布的不均衡问题，并且进一步提高了模型的收敛速度。（子网络）

PME模型通用性强，可适用于任意的异质网。

在Yelp数据集上进行了两个实验，效果好于state-of-the-art。

 

这篇文章的模型很简洁易懂，在如何优化这方面进行了比较深刻的研究，针对正负样本的采样分别提出了两个新策略。

本文的思想：分别在节点空间和关系空间构建节点和关系的embedding，而不是将节点和关系的embedding映射到同一空间中。这点和HEER模型很像，两篇文章都发表在了KDD2018。

两者区别为：

HEER只考虑了一阶邻居，而PME考虑了一阶和二阶相似性；

HEER是基于点积运算的，而PME将欧氏距离作为度量；

HEER从HIN的语义不兼容性入手，而PME从HIN的度量学习入手。