参数估计的计算方法
参数估计的计算方法
- 极大后验(MAP)及拉普拉斯逼近
- 基于马尔可夫链的蒙特卡洛参数推断(MCMC)
- 期望极大化(EM)
(参数估计所有内容)
极大后验(MAP)及拉普拉斯逼近
极大后验估计:
MAP是通过确定后验分布的极大值得到的,在点估计中的表达式为: MAP 估计可等效为能量函数的极小值:
MAP 估计可等效为能量函数的极小值:
 其中,能量函数表达式为:
其中,能量函数表达式为:
![]() 参数的极大似然估计即为一种标准先验概率满足下式的MAP估计:
参数的极大似然估计即为一种标准先验概率满足下式的MAP估计:
![]()
能量函数的极小值可通过多种基于无梯度或梯度的广义最优算法计算得到。
若要利用基于梯度的广义最优化算法,需要计算能量函数的导数。计算能量函数导数有两种方法:
1). 对能量函数的递归方程用一种特殊的方法进行微分,所得的结果称为灵敏度函数,可由类似于滤波过程中递归方程计算得到。
2). 利用Fisher特性,将能量函数的梯度表示为平滑分布所有数据对数似然导数的期望值。该方法相比于直接微分法优点在于不要计算额外的递归方程。
MAP估计的缺点:该方法实际运用了狄拉克 δ \bm{\delta} δ 方程逼近后验分布,即:
![]() 从而忽略了后验分布的变化。
从而忽略了后验分布的变化。
拉普拉斯逼近法:
利用能量函数的二阶导数(Hessian) 实现对后验分布的高斯逼近,表达式为:
![]() 式中, H ( θ ^ M A P ) \bm{H(\hat\theta^{MAP})} H(θ^MAP) 为 MAP 估计值出的 Hessian 矩阵。该方法需要计算或者逼近能量函数的二阶导数。
式中, H ( θ ^ M A P ) \bm{H(\hat\theta^{MAP})} H(θ^MAP) 为 MAP 估计值出的 Hessian 矩阵。该方法需要计算或者逼近能量函数的二阶导数。
基于马尔可夫链的蒙特卡洛参数推断(MCMC)
MH算法:
Metropolis-Hastings(MH)算法是最为常见的一种MCMC方法。MH引入建议密度 q ( θ ( i ) ∣ θ ( i − 1 ) ) \bm{q(\theta^{(i)}|\theta^{(i-1)})} q(θ(i)∣θ(i−1)),通过结合已知采样点 θ ( i − 1 ) \bm{\theta^{(i-1)}} θ(i−1),给出新的建议采样点 θ ( i ) \bm{\theta^{(i)}} θ(i)。
MH算法步骤为:
首选由任意初始分布得到起始点 θ ( 0 ) \bm{\theta^{(0)}} θ(0)。
然后,对于 i = 1 , 2 , ⋅ ⋅ ⋅ , N \bm{i=1,2,\cdot\cdot\cdot,N} i=1,2,⋅⋅⋅,N,有
1). 从建议密度中选择一个参考点 θ ∗ \bm{\theta^{*}} θ∗:
![]() 2). 计算接受概率:
2). 计算接受概率:
 3). 产生均匀分布随机变量 u ∼ U ( 0 , 1 ) \bm{u \sim U(0,1)} u∼U(0,1),并令:
3). 产生均匀分布随机变量 u ∼ U ( 0 , 1 ) \bm{u \sim U(0,1)} u∼U(0,1),并令:
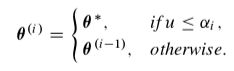
Metropolis算法为Metropolis-Hastings算法的一种特例,其建议分布为对称的,即 q ( θ ( i ) ∣ θ ( i − 1 ) ) = q ( θ ( i − 1 ) ∣ θ ( i ) ) \bm{q(\theta^{(i)}|\theta^{(i-1)})}=\bm{q(\theta^{(i-1)}|\theta^{(i)})} q(θ(i)∣θ(i−1))=q(θ(i−1)∣θ(i)),此时,接受概率缩减为:
![]()
建议分布的选取对Metropolis-Hastings算法的性能影响较大,通常采用高斯部分作为建议分布。即:
![]() 式中, ∑ i − 1 \bm{\sum^{i-1}} ∑i−1 为合适的协方差矩阵。
式中, ∑ i − 1 \bm{\sum^{i-1}} ∑i−1 为合适的协方差矩阵。
选定协方差矩阵其中一种方法是自适应马尔可夫链蒙特卡洛法( A M C M C \bm{AMCMC} AMCMC),该方法可以载解算 M C M C \bm{MCMC} MCMC时,自动调整所需要的高斯建议分布协方差阵。
A M C M C \bm{AMCMC} AMCMC 的思想为:利用先前采样点产生的协方差阵作为后验分布实际协方差阵的估计值。在已知先前的协方差矩阵的情况下,就可以计算建议分布的协方差阵。
RAM(robust adaptive Metropolis)算法:
RAM步骤为:
1). 有初始分布 p 0 ( θ ) \bm{p_0(\theta)} p0(θ) 获得 θ ( 0 ) \bm{\theta^{(0)}} θ(0),利用初始协方差阵的下三角阵 C h o l l e s k y \bm{Chollesky} Chollesky 因子对 S 0 \bm{S_0} S0 进行初始化。
2). 获取一个采样点 θ ∗ = θ i − 1 + S i − 1 r i , r i ∼ N ( 0 , I ) \bm{\theta^*=\theta_{i-1}+S_{i-1}r_i},r_i\sim N(0,I) θ∗=θi−1+Si−1ri,ri∼N(0,I)。
3). 计算接受概率:
![]() 4). 从均匀分布 U ( 0 , 1 ) \bm{U(0,1)} U(0,1) 中采样的到一个服从均匀分布的随机变量 u \bm{u} u。
4). 从均匀分布 U ( 0 , 1 ) \bm{U(0,1)} U(0,1) 中采样的到一个服从均匀分布的随机变量 u \bm{u} u。
5).
 6). 计算下三角矩阵 S i \bm{S_i} Si,使得该矩阵满足对角线元素为正,且该阵满足:
6). 计算下三角矩阵 S i \bm{S_i} Si,使得该矩阵满足对角线元素为正,且该阵满足:
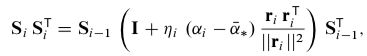 式中, { η } i ≥ 1 ⊂ ( 0 , 1 ] \bm{\{\eta\}_{i\ge1}\subset(0,1]} {η}i≥1⊂(0,1],为一个自适应步长序列,并逐渐衰减为零。可任意选取,在其他文献中给出一个选取建议: η i = i − γ , γ ∈ ( 1 / 2 , 1 ] \bm{\eta_i=i^{- \gamma},\gamma\in(1/2,1]} ηi=i−γ,γ∈(1/2,1]。
式中, { η } i ≥ 1 ⊂ ( 0 , 1 ] \bm{\{\eta\}_{i\ge1}\subset(0,1]} {η}i≥1⊂(0,1],为一个自适应步长序列,并逐渐衰减为零。可任意选取,在其他文献中给出一个选取建议: η i = i − γ , γ ∈ ( 1 / 2 , 1 ] \bm{\eta_i=i^{- \gamma},\gamma\in(1/2,1]} ηi=i−γ,γ∈(1/2,1]。
7). 令 i ← i + 1 \bm{i\leftarrow i+1} i←i+1,跳至步骤2),直到获取足够多的采样点。
期望极大化(EM)
E M \bm{EM} EM 算法适用于边缘似然无法计算但仍能计算得到似然函数下界的情形。设 q ( x 0 : T ) \bm{q(x_{0:T})} q(x0:T) 为状态的任意概率密度函数,则有:
![]() 式中,函数 F \bm{F} F 的定义为:
式中,函数 F \bm{F} F 的定义为:
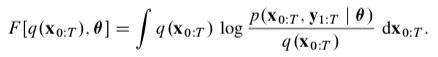
E M \bm{EM} EM 算法中国最重要的就是通过迭代最大化下界 F [ q ( x 0 : T ) , θ ] \bm{F[q(x_{0:T}),\theta]} F[q(x0:T),θ],进而实现 l o g p ( y 1 : T ∣ θ ) \bm{logp(y_{1:T}|\theta)} logp(y1:T∣θ) 的最大化。
简易的EM算法:
对函数 F \bm{F} F 的最大化,可通过协调提升下述步骤实现:
假设初始值为: q ( 0 ) , θ ( 0 ) \bm{q^{(0)},\theta^{(0)}} q(0),θ(0)。
对于 n = 0 , 1 , 2 , ⋅ ⋅ ⋅ \bm{n=0,1,2,\cdot\cdot\cdot} n=0,1,2,⋅⋅⋅,执行如下步骤:
1). E-步骤:获取:
![]() 2). M-步骤:获取:
2). M-步骤:获取:
![]()
为实现 E M \bm{EM} EM 算法,上式的极大化必行是可行的,所幸在其他文献中给出 E \bm{E} E 步骤极大化后的结果:
![]() 将上式带入 F \bm{F} F 函数中,得:
将上式带入 F \bm{F} F 函数中,得:

由于在实行 M \bm{M} M 步骤中,上式右边第二项与 θ \bm{\theta} θ 无关,故极大化 函数 F \bm{F} F 就得等价于对等式右边第一项对极大化,因此,在 E M \bm{EM} EM 算法中,可表示为:
![]() 上式为 E M \bm{EM} EM 算法得到关于 p ( x 0 : T , y 0 : T ∣ θ ) \bm{p(x_{0:T},y_{0:T}|\theta)} p(x0:T,y0:T∣θ) 的期望, p ( x 0 : T , y 0 : T ∣ θ ) \bm{p(x_{0:T},y_{0:T}|\theta)} p(x0:T,y0:T∣θ)是在参数 θ \bm{\theta} θ 条件下关于全部状态量和量测量的联合后验似然分布。
上式为 E M \bm{EM} EM 算法得到关于 p ( x 0 : T , y 0 : T ∣ θ ) \bm{p(x_{0:T},y_{0:T}|\theta)} p(x0:T,y0:T∣θ) 的期望, p ( x 0 : T , y 0 : T ∣ θ ) \bm{p(x_{0:T},y_{0:T}|\theta)} p(x0:T,y0:T∣θ)是在参数 θ \bm{\theta} θ 条件下关于全部状态量和量测量的联合后验似然分布。
E M \bm{EM} EM 算法:
假设初始值为 θ ( 0 ) \bm{\theta^{(0)}} θ(0)。对于 n = 0 , 1 , 2 , ⋅ ⋅ ⋅ \bm{n=0,1,2,\cdot\cdot\cdot} n=0,1,2,⋅⋅⋅,执行如下步骤:
1). E-步骤:计算 Q ( θ , θ ( n ) ) \bm{\mathcal{Q(\theta,\theta^{(n)})}} Q(θ,θ(n))。
2). M-步骤:计算:
![]() 结合下式:状态空间模型的马尔可夫链结构:
结合下式:状态空间模型的马尔可夫链结构:
 完全数据的对数似然表达式为:
完全数据的对数似然表达式为:
 因此, Q \bm{\mathcal{Q}} Q 的表达式及上述算法的 E \bm{E} E 步骤可以简化为:
因此, Q \bm{\mathcal{Q}} Q 的表达式及上述算法的 E \bm{E} E 步骤可以简化为:
![]() 式中:
式中:
 上式均为关于平滑分布的期望,即可不必在计算完全后验分布的期望。
上式均为关于平滑分布的期望,即可不必在计算完全后验分布的期望。
在 E M \bm{EM} EM 算法的 E \bm{E} E 步骤中,需要对 Q \bm{\mathcal{Q}} Q 的表达式关于参数 θ \bm{\theta} θ 的极大化。
实用的方法为将梯度设为零,求的此时极大值时候的 θ \bm{\theta} θ 取值:

E M \bm{EM} EM 算法,
E \bm{E} E 步骤:利用上一步得到的表达式 Q ( θ , θ n ) \bm{\mathcal{Q(\theta,\theta^n)}} Q(θ,θn) 求出满足表达式 Q ( θ , θ n ) \bm{\mathcal{Q(\theta,\theta^n)}} Q(θ,θn) 极大值的 参数 θ n \bm{\theta^n} θn,
M \bm{M} M 步骤:将 E \bm{E} E 步骤求出的参数 θ n \bm{\theta^n} θn 作为下一步已知的值 θ n + 1 \bm{\theta^{n+1}} θn+1 带入表达式 Q ( θ , θ n ) \bm{\mathcal{Q(\theta,\theta^n)}} Q(θ,θn) 中得到 Q ( θ , θ n + 1 ) \bm{\mathcal{Q(\theta,\theta^{n+1})}} Q(θ,θn+1),进而最大化函数 F \bm{F} F 的下限。
循环重复 E , M \bm{E,M} E,M 步骤,直到满足要求。