Bidirectional Attentive Memory Networks for Question Answering over Knowledge Bases

Knowledge Bases)

origin

2019 naacl
yu Chen
Rensselaer Polytechnic Institute
Lingfei Wu
IBM Research
Mohammed J. Zaki
Rensselaer Polytechnic Institute

代码实现

motivation

本文主要研究基于知识图谱的问答问题。KGQA的方法大致可以分为基于语义分割和信息检索的方法。基于语义分割的方法是建立一个语义分割器，将问题转化成可以在KG上执行的逻辑表达式的形式。这类方法通常是预先一组词汇触发器或者规则，因此限制领域以及规模。基于信息检索的方式根据从问题里传达的信息直接从KG中直接检索。
　　过去解决KGQA问题的基于信息检索的方法主要是通过基于embedding的方法，这类方法往往忽略了问题和KG之间的交互，例如实体的类型、 关系路径以及上下文。本文提出了双向注意力内存网络用于KGQA，增加问题和知识库的交互，知识库可以更好的帮助理解问题，问题可以更加关注知识库中更重要的部分。BAMnet 在WebQestion 数据集上取得了SOTA效果。

model

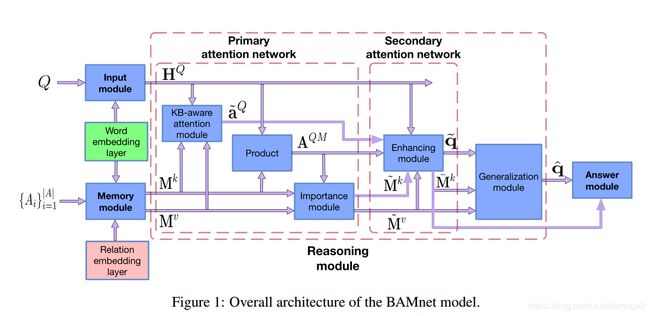
整体上分为input module 、memory module、reasoning module 和　answer module等四个模块。接下来详细介绍每个模块

input module:
输入一个问题$Q$，是一个word embedding　序列，使用Bi-lstm 模型编码问题，得到问题编码$H^Q\in R^{d\ast |Q|}$
memory module:
１．确定候选答案集合：
　首先确定topic entity , 和topic entity 在h hops　联通的所有实体构成的集合 $\{A_i{\}}_{i=1}^{|A|}$
２．知识图谱表示：
answer type: 实体的类型和问题也是息息相关的，　比如问题中含有where等词汇，则concept of location 可能是候选答案。　使用Bi-lstm 编码entity description 得到一个d 维的向量 $H_i^{t_1}$
answer path :　topic entity 和　candidate entity 之间的关系路径　作为answer path , 　本文使用了两种方式来编码路径　第一种使用bi-lstm 编码关系路径得到$H_i^{p_1}$ 　第二种使用relation embedding 的平均值$H_i^{p_2}$ ,　二者的连接作为　answer path 的编码
answer context: 使用candidate answer 周边的实体(例如candidate 的兄弟节点)帮助回答带有约束的问题。　对于没有约束的问题，引入answer context 是没有必要的，而且会增加一些噪音。　本文采用下面两个策略来克服这个问题：１．使用了一个重要性模块(importance module) 2. 只考虑和问题有重叠的context节点
3. key-value momory　
本文使用key-value memory 存储候选答案。


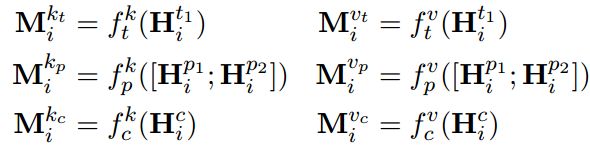
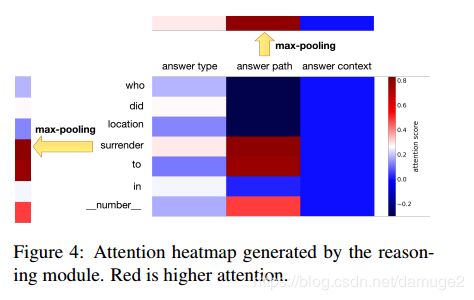
推理模块：
推理模块包括了一般化模块和两层attention: primary attention 和 secondary attention layer
首先介绍primary attention layer：包括kb-aware attention module 和　importance module
两个模块作用分别是 依据知识库更好的理解问题　以及　根据问题捕捉知识库中更重要的部分
secondary attention 的作用是利用注意力机制进一步增加问题和知识库的互动。

１．kb-aware attention module:
问题的每个部分重要性并不是相同的，因此首先使用self-attention将问题序列映射成一个d 维的向量q

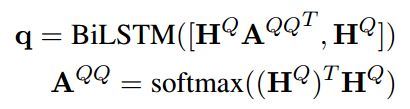
之后再通过一个AddAtt


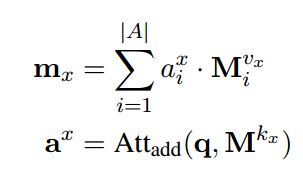
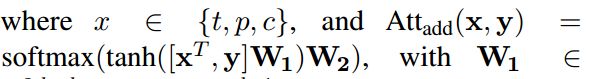
这样可以得到KB summary

接下来计算问题中每个单词和KB summary 之间的attention $A^{Qm}={H^Q}^{T}m$
接下来在最后一个维度上应用max pooling 操作，　$a_i^Q=ma{x}_j{A}_{ij}^{Qm}$
之后使用softmax 得到$a^Q$

2. importance module
   
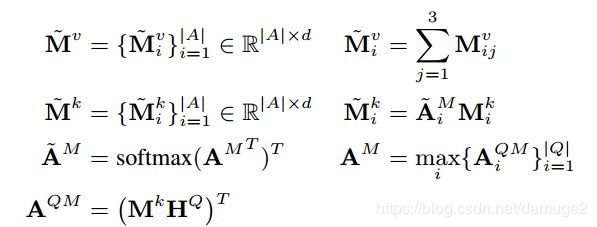
3. enhance 模块
   　　再使用两个注意力更好的表示问题Ｑ和KB
   KB-enhance:
   
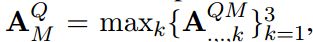
   对$A_M^Q$进行规范化得到$A_M^Q$，之后可以得到一个kb-enhanced 问题表示：
   
   类似的可以得到一个question-enhanced kb 表示
   
   ４．一般化模块
   
   先使用一个attention 机制，　之后再通过个GRU模型，最后通过一个残差连接层

回答模块：
计算问题q的表示以及所有答案的表示之间的分数，按照大小顺序排序
$S(\hat{q},\overline{M_i^k})$ 使用公式$s(q,a)=q^T\cdot a$

train and test

loss function:

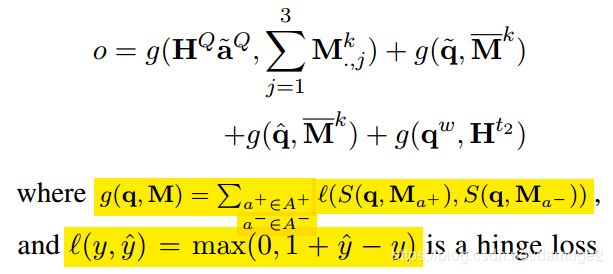
问题和KB 的中间表示　和最后的表示都可以参与到损失函数的构建中
此外，还可以用$q^{\omega }$ 表示问题，是一个16维的疑问词（包括“which”, “what”, “who”, “whose”, “whom”,
“where”, “when”, “how”, “why” and “whether”)
候选答案$A_i$使用实体类型$H_i^{t_2}$表示

测试时：　选择与评分最高的答案评分相差在一定区间的答案认为是好的答案

topic entity prediction:
使用工具 Freebase Search API and　S-MART 抽取topic entity candidate $\{C_i{\}}_{i=1}^{|C|}$, 使用CNN 编码问题$e$和topic entity(包括实体名、实体类型、周围关系) 得到向量$[C_i^n,C_i^t,C_i^{r_1}]$,此外平均周围关系得到另外一个embedding$C_i^{r_2}$。
使用一个线性映射：

使用上面的generate module 得到一个更新的问题向量表示$\hat{e}$
损失函数为$o=g(e,P_i^k)+g(\hat{e},p_i^k)$

experiment

消融测试：

可解释性分析：