文科生都能看懂的机器学习教程:梯度下降、线性回归、逻辑回归(附动图解释)...
![]()
来源:新智元
本文约4200字,建议阅读10+分钟。
本文浅显易懂的方式讲解机器学习,力求让没有理科背景的读者都能看懂。
[ 导读 ]虽然在Coursera、MIT、UC伯克利上有很多机器学习的课程,包括吴恩达等专家课程已非常经典,但都是面向有一定理科背景的专业人士。本文试图将机器学习这本深奥的课程,以更加浅显易懂的方式讲出来,让没有理科背景的读者都能看懂。
把复杂的东西简单化,让非专业人士也能短时间内理解,并露出恍然大悟的表情,是一项非常厉害的技能。
举个例子。你正在应聘机器学习工程师,面对的是文科出身的HR,如果能在最短时间内让她了解你的专业能力,就能极大地提升面试成功率。
现在,机器学习这么火,想入行的人越来越多,然而被搞糊涂的人也越来越多。因为大众很难理解机器学习是干吗的?那些神秘拗口的概念,比如逻辑回归、梯度下降到底是什么?
一个23岁的药物学专业的学生说,当他去参加机器学习培训课程的时候,感觉自己就家里那位不懂现代科技的奶奶。
于是一名叫Audrey Lorberfeld的毕业生,试图将大众与机器学习之间的鸿沟,亲手填补上。于是有了这个系列文章。
本系列第一讲:
梯度下降
线性回归
逻辑回归
算法 vs 模型
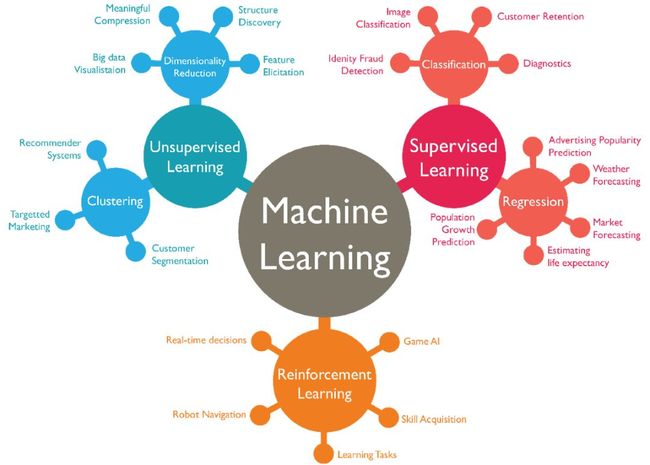
在理解开始了解机器学习之前,我们需要先搞懂两个基础概念:算法和模型。
我们可以把模型看做是一个自动售货机,输入(钱),输出(可乐)。算法是用来训练这个模型的,
模型根据给定的输入,做出对应的决策获得预期输出。例如,一个算法根据投入的金额,可乐的单价,判断钱够不够,如果多了该找多少钱。
总而言之,算法是模型背后的数学生命力。没有模型,算法只是一个数学方程式。模型的不同,取决于用的算法的不同。
梯度下降/最佳拟合线
(虽然这个传统上并不被认为是一种机器学习算法,但理解梯度对于了解有多少机器学习算法可用,及如何优化至关重要。)梯度下降帮助我们根据一些数据,获得最准确的预测。
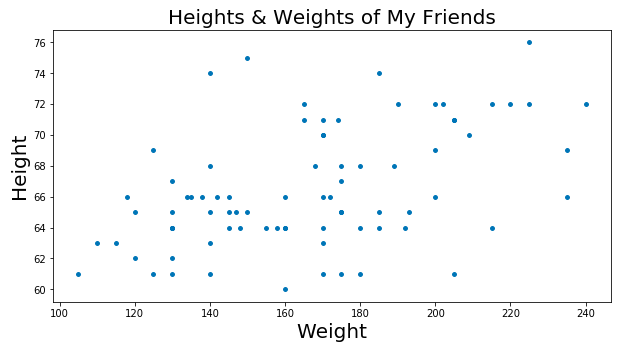
举个例子。你有一个大的清单,列出每个你认识的人身高体重。然后做成下面这种分布图:
图上面的数字比较奇怪?不用在意这些细节。
现在,小区居委会要举办一个根据身高猜体重的比赛,赢的人发红包。就用这张图。你怎么办?
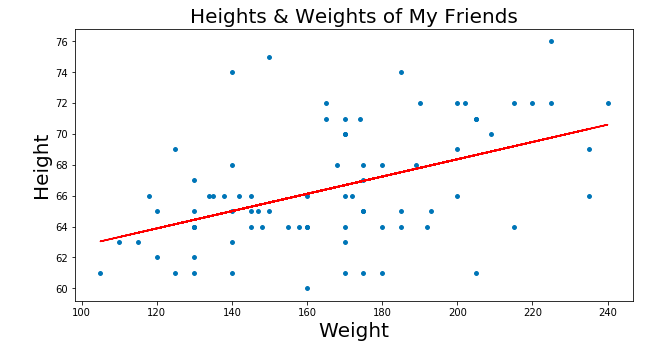
你可能会想在图上画一根线,这个线非常完美的给出了身高和体重的对应关系。
比如,根据这条完美线,身高1.5米的人体重基本在60斤左右。啊那么,这根完美线是怎么找出来呢?答:梯度下降。
我们先提一个概念叫RSS(the residual sum of squares)。RSS是点和线之间差异的平方和,这个值代表了点和线的距离有多远。梯度下降就是找出RSS的最小值。
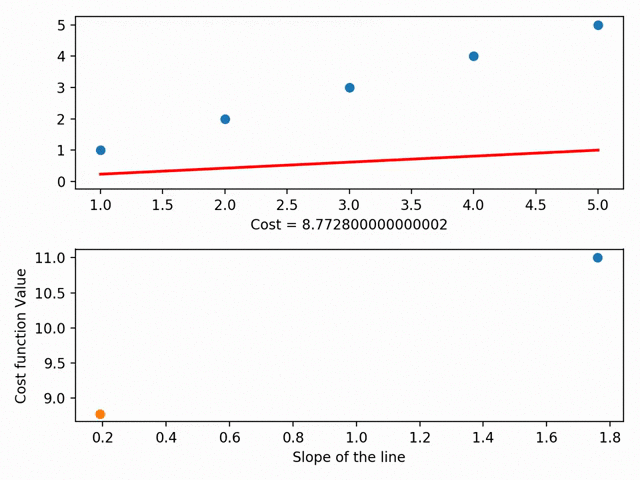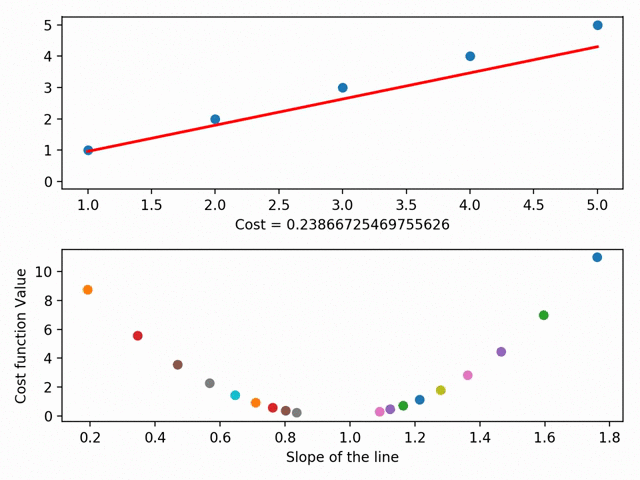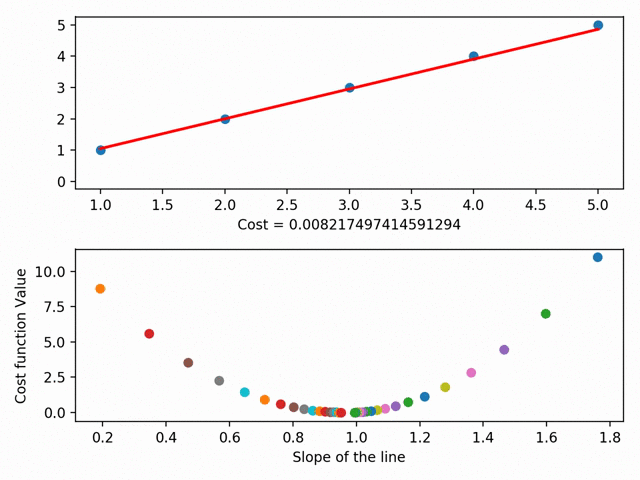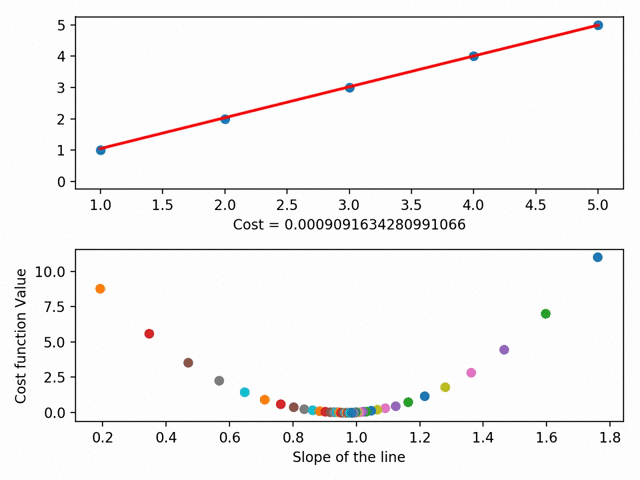
我们把每次为这根线找的不同参数进行可视化,就得到了一个叫做成本曲线的东西。这个曲线的地步,就是我们的RSS最小值。
Gradient Descent可视化(使用MatplotLib)
来自不可思议的数据科学家Bhavesh Bhatt
梯度下降还有其他的一些细分领域,比如“步长”和“学习率”(即我们想要采取什么方向到底部的底部)。
总之,我们通过梯度下降找到数据点和最佳拟合线之间最小的空间;而最佳你和线是我们做预测的直接依据。
线性回归
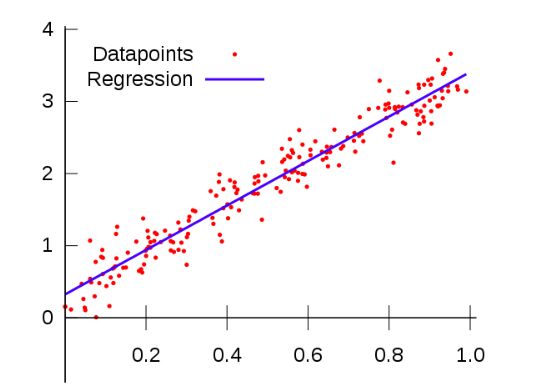
线性回归是分析一个变量与另外一个或多个变量(自变量)之间,关系强度的方法。
线性回归的标志,如名称所暗示的那样,即自变量与结果变量之间的关系是线性的,也就是说变量关系可以连城一条直线。
这看起来像我们上面做的!这是因为线性回归中我们的“回归线”之前的最佳实践线。最佳拟合线显示了我们的点之间最佳的线性关系。反过来,这使我们能够做出预测。
关于线性回归的另一个重点是,结果变量或“根据其他变量而变化的”变量(有点绕哈)总是连续的。但这意味着什么?
假设我们想测量一下纽约州影响降雨的因素:结果变量就是降雨量,就是我们最关系的东西,而影响降水的自变量是海拔。
如果结果变量不是连续的,就可能出现在某个海拔,没有结果变量,导致我们没办法做出预测。
反之,任意给定的海拔,我们都可以做出预测。这就是线性回归最酷的地方!
岭回归与LASSO回归
现在我们知道什么是线性回归,接下来还有更酷的,比如岭回归。在开始理解岭回归之前,我们先来了解正则化。
简单地说,数据科学家使用正则化,确保模型只关注能够对结果变量产生显著影响的自变量。
但是那些对结果影响不显著的自变量会被正则忽略吗?当然不会!原因我们后面再展开细讲。
原则上,我们创建这些模型,投喂数据,然后测试我们的模型是否足够好。
如果不管自变量相关也好不相关都投喂进去,最后我们会发现模型在处理训练数据的时候超棒;但是处理我们的测试数据就超烂。
这是因为我们的模型不够灵活,面对新数据的时候就显得有点不知所措了。这个时候我们称之为“Overfit”,即“过拟合”。
接下来我们通过一个过长的例子,来体会一下过拟合。
比方说,你是一个新妈妈,你的宝宝喜欢吃面条。几个月来,你养成了一个在厨房喂食并开窗的习惯,因为你喜欢新鲜空气。
接着你的侄子给宝宝一个围裙,这样他吃东西就不会弄得满身都是,然后你又养成了一个新的习惯:喂宝宝吃面条的时候,必须穿上围裙。
随后你又收养了一只流浪狗,每次宝宝吃饭的时候狗就蹲在婴儿椅旁边,等着吃宝宝掉下来的面条。
作为一个新妈妈,你很自然的会认为,开着的窗户+围裙+婴儿椅下面的狗,是让你的宝宝能够开心吃面条的必备条件。
直到有一天你回娘家过周末。当你发现厨房里没有窗户你有点慌;然后你突然想起来走的匆忙围裙也没带;最要命的是狗也交给邻居照看了,天哪!
你惊慌到手足无措以至于忘记给宝宝喂食,就直接把他放床上了。看,当你面对一个完全新的场景时你表现的很糟糕。而在家则完全是另外一种画风了。
经过重新设计模型,过滤掉所有的噪音(不相关的数据)后你发现,其实宝宝仅仅是喜欢你亲手做的面条。
第二天,你就能坦然的在一个没有窗户的厨房里,没给宝宝穿围裙,也没有狗旁边,开开心心的喂宝宝吃面条了。
这就是机器学习的正则化所干的事情:让你的模型只关注有用的数据,忽略干扰项。
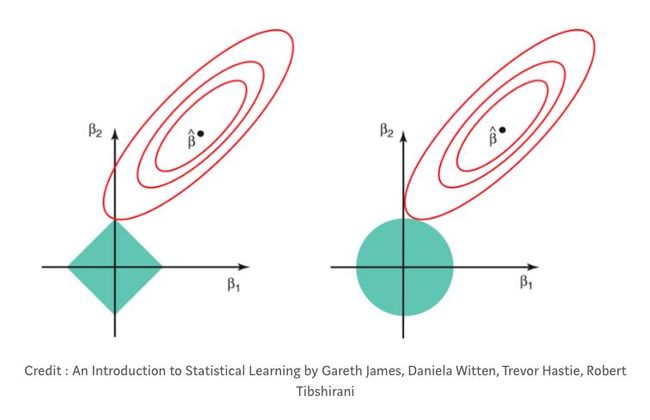
在左边:LASSO回归(你可以看到红色梯级表示的系数在穿过y轴时可以等于零)
在右边:岭回归(你可以看到系数接近,但从不等于零,因为它们从不穿过y轴)
图片来源:Prashant Gupta的“机器学习中的正规化”
在各种正规化的,有一些所谓的惩罚因子(希腊字母拉姆达:λ)。这个惩罚因子的作用是在数学计算中,缩小数据中的噪声。
在岭回归中,有时称为“L2回归”,惩罚因子是变量系数的平方值之和。惩罚因子缩小了自变量的系数,但从来没有完全消除它们。这意味着通过岭回归,您的模型中的噪声将始终被您的模型考虑在内。
另一种正则化是LASSO或“L1”正则化。在LASSO正则化中,只需惩罚高系数特征,而不是惩罚数据中的每个特征。
此外,LASSO能够将系数一直缩小到零。这基本上会从数据集中删除这些特征,因为它们的“权重”现在为零(即它们实际上是乘以零)。
通过LASSO回归,模型有可能消除大部分噪声在数据集中。这在某些情况下非常有用!
逻辑回归
现在我们知道,线性回归=某些变量对另一个变量的影响,并且有2个假设:
结果变量是连续的;
变量和结果变量之间的关系是线性的。
但如果结果变量不是连续的而是分类的呢?这个时候就用到逻辑回归了。
分类变量只是属于单个类别的变量。比如每一周都是周一到周日7个日子,那么这个时候你就不能按照天数去做预测了。
每周的第一天都是星期一,周一发生的事情,就是发生在周一。没毛病。
逻辑回归模型只输出数据点在一个或另一个类别中的概率,而不是常规数值。这也是逻辑回归模型主要用于分类的原因。
在逻辑回归的世界中,结果变量与自变量的对数概率(log-odds)具有线性关系。
比率(odds)
逻辑回归的核心就是odds。举个例子:
一个班里有19个学生,其中女生6个,男生13个。假设女性通过考试的几率是5:1,而男性通过考试的几率是3:10。这意味着,在6名女性中,有5名可能通过测试,而13名男性中有3名可能通过测试。
那么,odds和概率(probability)不一样吗?并不。
概率测量的是事件发生的次数与所有事情发生的总次数的比率,例如,投掷40次投币10次是正面的概率是25%;odds测量事件发生的次数与事件的次数的比率,例如抛掷30次有10次是正面,odds指的是10次正面:30次反面。
这意味着虽然概率总是被限制在0-1的范围内,但是odds可以从0连续增长到正无穷大!
这给我们的逻辑回归模型带来了问题,因为我们知道我们的预期输出是概率(即0-1的数字)。
那么,我们如何从odds到概率?
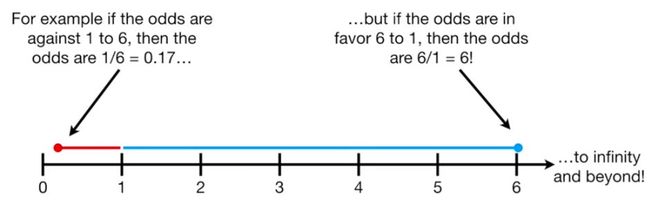
让我们想一个分类问题,比如你最喜欢的足球队和另一只球队比赛,赢了6场。你可能会说你的球队失利的几率是1:6,或0.17。
而你的团队获胜的几率,因为他们是一支伟大的球队,是6:1或6。如图:
图片来源:
https://www.youtube.com/watch?v=ARfXDSkQf1Y
现在,你不希望你的模型预测你的球队将在未来的比赛中取胜,只是因为他们过去获胜的几率远远超过他们过去失败的几率,对吧?
还有更多模型需要考虑的因素(可能是天气,也许是首发球员等)!因此,为了使得odds的大小均匀分布或对称,我们计算出一些称为对数比率(log-odds)的东西。
log-odds
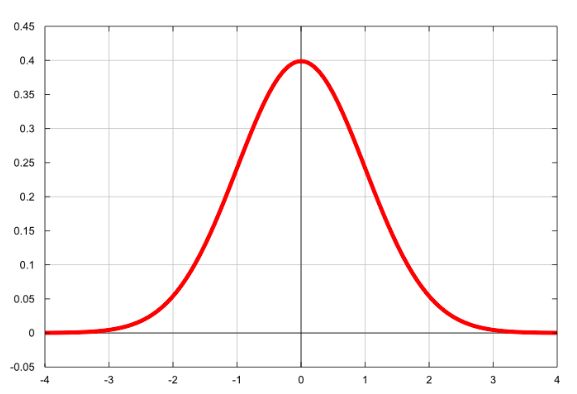
我们所谓的“正态分布”:经典的钟形曲线!
Log-odds是自然对数odds的简写方式。当你采用某种东西的自然对数时,你基本上可以使它更正常分布。当我们制作更正常分布的东西时,我们基本上把它放在一个非常容易使用的尺度上。
当我们采用log-odds时,我们将odds的范围从0正无穷大转换为负无穷正无穷大。可以在上面的钟形曲线上看到这一点。
即使我们仍然需要输出在0-1之间,我们通过获取log-odds实现的对称性使我们比以前更接近我们想要的输出!
Logit函数
“logit函数”只是我们为了得到log-odds而做的数学运算!
恐怖的不可描述的数学。呃,我的意思是logit函数。
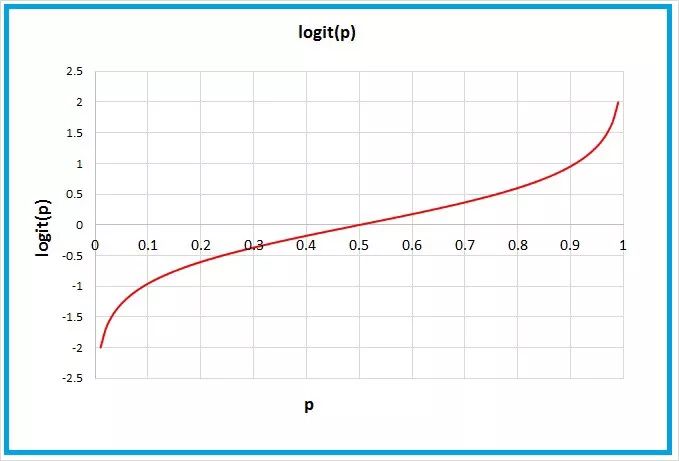
logit函数,用图表绘制
正如您在上面所看到的,logit函数通过取其自然对数将我们的odds设置为负无穷大到正无穷大。
Sigmoid函数
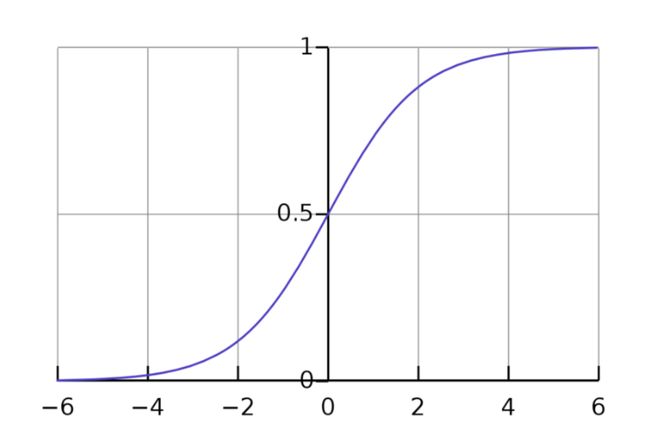
好的,但我们还没有达到模型给我们概率的程度。现在,我们所有的数字都是负无穷大到正无穷大的数字。名叫:sigmoid函数。
sigmoid函数,以其绘制时呈现的s形状命名,只是log-odds的倒数。通过得到log-odds的倒数,我们将我们的值从负无穷大正无穷大映射到0-1。反过来,让我们得到概率,这正是我们想要的!
与logit函数的图形相反,其中我们的y值范围从负无穷大到正无穷大,我们的sigmoid函数的图形具有0-1的y值。好极了!
有了这个,我们现在可以插入任何x值并将其追溯到预测的y值。该y值将是该x值在一个类别或另一个类别中的概率。
最大似然估计
你还记得我们是如何通过最小化RSS(有时被称为“普通最小二乘法”或OLS法)的方法在线性回归中找到最佳拟合线的吗?
在这里,我们使用称为最大似然估计(MLE)的东西来获得最准确的预测。
MLE通过确定最能描述我们数据的概率分布参数,为我们提供最准确的预测。
我们为什么要关心如何确定数据的分布?因为它很酷!(并不是)
它只是使我们的数据更容易使用,并使我们的模型可以推广到许多不同的数据。
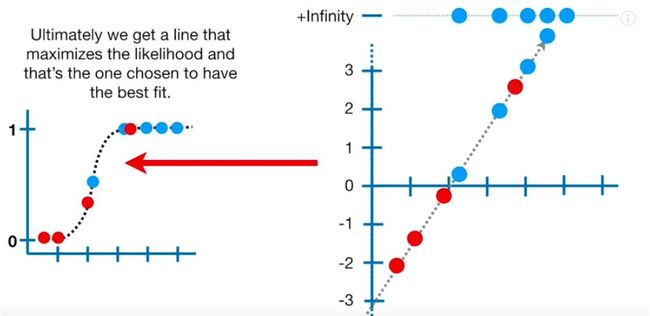
一般来说,为了获得我们数据的MLE,我们将数据点放在s曲线上并加上它们的对数似然。
基本上,我们希望找到最大化数据对数似然性的s曲线。我们只是继续计算每个log-odds行的对数似然(类似于我们对每个线性回归中最佳拟合线的RSS所做的那样),直到我们得到最大数量。
好了,到此为止我们知道了什么是梯度下降、线性回归和逻辑回顾,下一讲,由Audrey妹子来讲解决策树、随机森林和SVM。
参考链接:
https://towardsdatascience.com/machine-learning-algorithms-in-laymans-terms-part-1-d0368d769a7b
编辑:黄继彦
校对:林亦霖
![]()
![]()