cs224n学习笔记L3:Neural Networks
cs224n学习笔记L2:word vectors and word senses
文章目录
- 一、课程安排
- 1.1 近期安排
- 1.2 本节课安排
- 二、分类
- 2.1 分类介绍
- 2.2 传统方案分类
- 2.3 交叉熵(cross entropy)损失
- 2.4 传统ML优化方法
- 2.5 传统ML的问题
- 2.6 NLP分类
- 三、神经网络
- 3.1 人工神经元
- 3.2 神经网络的矩阵运算
- 3.3 为什么需要非线性激活函数f
- 四、命名实体识别(NER)
- 4.1 NER任务描述
- 4.2 NER难点
- 4.3 窗口分类器
- 4.4 softmax窗口分类器
- 4.5 计算过程
- 五、梯度计算
- 5.1 1-output 和 n-input的函数(标量对向量求导)
- 5.2 m-outputs 和 n-inputs的函数(向量对向量求导)
- 5.3 链式法则
- 5.4 常用求导公式
- 6. 反向传播(backpropagation)计算实例
- 6.1 网络拆解
- 6.2 局部误差信号和局部输入信号
一、课程安排
1.1 近期安排
- 第二周:神经网络基础、反向传播和nlp分类器
- 第三周:神经网络自然语言处理、依赖解析、概率语言模型
Chris Manning重申了这门课程难度较高,研究生级别的课程,希望同学们加把劲努力完成。鼓励同学们多查资料多看文献。
1.2 本节课安排
- 分类算法介绍
- 神经网络介绍
- 命名实体识别
- binary true vs corrupted(模型名)词窗口分类
- 矩阵计算介绍
二、分类
2.1 分类介绍
对于训练集 { x i , y i } N \{x_i, y_i\}^N {xi,yi}N:
- x i x_i xi为d维输入数据
- y i y_i yi为预测标签, 可例如情感类别、命名实体、买卖决策等,可能为单词或多个词构成的序列。
从直觉上理解分类,如下图,二维数据下,相当于学习一条分界直线将两类数据点尽可能分开。例如:使用固定二维词向量,logistics regression、线性决策边界

2.2 传统方案分类
训练softmax/logistics模型,学习权重 W ∈ R C × d W \in R^{C \times d} W∈RC×d(C为类别数)来决定一个超平面这里和前面的word vector计算是不是很像呢?对于每个输入数据x预测 P ( Y ∣ x ) = s o f t m a x ( W ⋅ x ) P(Y|x)=softmax(W\cdot x) P(Y∣x)=softmax(W⋅x), 即
p ( y ∣ x ) = e x p ( w y ⋅ x ) ∑ c ∈ C e x p ( w c ⋅ x ) p(y|x) = \frac{exp(w_y\cdot x)}{\sum_{c \in C}exp(w_c \cdot x)} p(y∣x)=∑c∈Cexp(wc⋅x)exp(wy⋅x)
我们的目标是要最大化正确类别的输出概率,等价于最小化正确类别输出概率的负对数:
− l o g p ( y t r u e ∣ x ) = − l o g e x p ( w y t r u e ⋅ x ) ∑ c ∈ C e x p ( w c ⋅ x ) -log p(ytrue|x) = -log \frac{exp(w_{ytrue}\cdot x)}{\sum_{c \in C}exp(w_c \cdot x)} −logp(ytrue∣x)=−log∑c∈Cexp(wc⋅x)exp(wytrue⋅x)
2.3 交叉熵(cross entropy)损失
这是一个非常常见的损失函数,基本形式如下
H ( p , q ) = − ∑ c = 1 C p c log ( q c ) H(p,q) = -\sum_{c=1}^C p_c \textup{log}(q_c) H(p,q)=−c=1∑Cpclog(qc)
对于训练集,这里p是真实概率分布,也就是数据集中的标签y, 而q是我们模型前向计算得到的概率分布,通常是从softmax激活函数得到。由于分类标签p通常为一个one-hot向量,所以上面的损失函数的求和其实只有一项生效,即
H ( p , q ) = − ∑ c = 1 C p c log ( q c ) = − l o g ( q t r u e ) H(p,q) = -\sum_{c=1}^C p_c \textup{log}(q_c)=-log(q_{true}) H(p,q)=−c=1∑Cpclog(qc)=−log(qtrue)
在整个数据集 { x i , y i } N \{x_i, y_i\}^N {xi,yi}N上的交叉熵损失:
J ( θ ) = − 1 N ∑ i = 1 N l o g e x p ( w y t r u e x ) ∑ c ∈ C e x p ( w c x ) J(\theta) = -\frac{1}{N}\sum_{i=1}^N log \frac{exp(w_{ytrue}x)}{\sum_{c \in C}exp(w_cx)} J(θ)=−N1i=1∑Nlog∑c∈Cexp(wcx)exp(wytruex)
为了表示方便,下面用符号 f y = W y x 、 f = W x f_y = W_yx、f = Wx fy=Wyx、f=Wx 替代表达。
2.4 传统ML优化方法
通常把权重的每一行看作一个向量参数,那么权重相当于一个列向量:
θ = W = [ W 1 ⋮ W n ] = W ( : ) ∈ R C × d \theta =W = \left[ \begin{matrix} W_1 \\ \vdots \\ W_n\\ \end{matrix} \right] = W(:) \in R^{C \times d} θ=W=⎣⎢⎡W1⋮Wn⎦⎥⎤=W(:)∈RC×d
这不正是上一节课的词向量矩阵U?然后通过更新如下参数来更新决策边界:
∇ θ J ( θ ) = [ ∇ W 1 ⋮ ∇ W n ] \nabla_{\theta}J(\theta) = \left[ \begin{matrix} \nabla _{W_1} \\ \vdots \\ \nabla _{W_n}\\ \end{matrix} \right] ∇θJ(θ)=⎣⎢⎡∇W1⋮∇Wn⎦⎥⎤
2.5 传统ML的问题
由于简单的softmax决定一个线性决策平面,这无法有效的解决如下非线性复杂问题。

2.6 NLP分类
nlp与传统问题不同,需要同时学习权重W和输入向量x(表达学习maybe)。
三、神经网络
3.1 人工神经元
神经元包含的参数为W, b=b, 通过激活函数可以定义神经元的功能,使用sigmod作为激活函数,那么神经元被定义为逻辑回归。
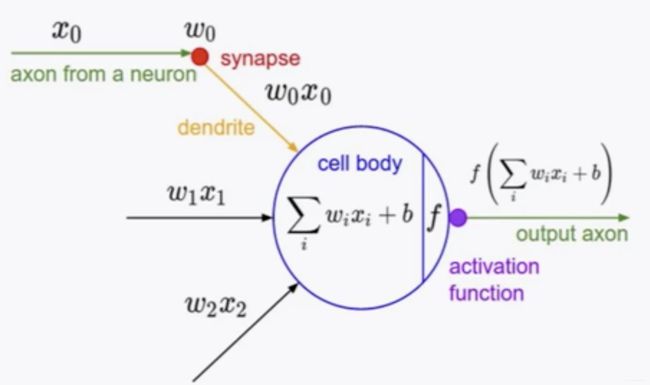
将一个输入向量输入到一批逻辑回归函数(sigmod神经元),那么得到的输出就是一个向量。对于上面的二分类问题,如果使用如下多层模型,那么可以得到一个扭曲的分类边界从而更好的分类,但我们不能再像传统ML算法那样理解模型中间层的物理意义。

3.2 神经网络的矩阵运算
a 1 = f ( W 11 x 1 + W 12 x 2 + W 13 x 3 + b 1 ) a 2 = f ( W 21 x 1 + W 22 x 2 + W 23 x 3 + b 2 ) … a _ { 1 } = f \left( W _ { 11 } x _ { 1 } + W _ { 12 } x _ { 2 } + W _ { 13 } x _ { 3 } + b _ { 1 } \right) \\ a _ { 2 } = f \left( W _ { 21 } x _ { 1 } + W _ { 22 } x _ { 2 } + W _ { 23 } x _ { 3 } + b _ { 2 } \right) \\ \dots a1=f(W11x1+W12x2+W13x3+b1)a2=f(W21x1+W22x2+W23x3+b2)…
这里f是激活函数 f ( [ z 1 , z 2 , z 3 ] ) = [ f ( z 1 ) , f ( z 2 ) , f ( z 3 ) ] f([z_1, z_2, z_3]) = [f(z_1), f(z_2), f(z_3)] f([z1,z2,z3])=[f(z1),f(z2),f(z3)],用矩阵表示就相当于:
z = W 3 × 4 x + b a = f ( z ) z = W^{3 \times 4}x+b\\ a = f(z) z=W3×4x+ba=f(z)
这里与我们前面的传统ML方法或词向量相比较,似乎是多了一个偏置项b。
3.3 为什么需要非线性激活函数f
使用函数估计来说明:
- 不适用非线性激活函数,深度神经网络只能进行线性变换
- 额外增加的层数也只会编码出一个简单的线性变换: W 1 W 2 x = W x W_1W_2x = Wx W1W2x=Wx
- 有了非线性激活函数,增加层数就可以拟合更复杂的函数。
四、命名实体识别(NER)
在这之前我们要先理解一个神经网络实际上相当于同时运行多个逻辑回归函数。
4.1 NER任务描述
- 定义:找到并分类文本中的实体名称


- 用途
- 检索文档中提到相实体的话题
- 问答系统中的答案通常为实体
- 很多有用的信息都隐藏在实体以及实体之间的关系中
- NER技术框架可以用于其他工作
- 通常NER后会衔接实体链接和标准化等工作。
4.2 NER难点
看两个例句:
- First National Bank Donates 2 Vans To Future School of Fort Smith.
- To find more about Zig Ziglar and read futures by other Creators Syndicate writers and …
- 难以确定实体边界:First National Bank 还是 National Bank?
- 难以确定一个词是不是实体:Future School 还是 future school?
- 难以分类一些稀有名词:Zig Ziglar是个什么鬼?(人名)
- 实体二义性?比如人名可能与机构名重名,如何区分?
4.3 窗口分类器
- Binary word window classification
- 一般很少对单个词进行分类
- 使用二元窗口分类器对上下文分类
- 语言可能出现歧义:“To sanction” can mean “to permit” or "to punish”,“To seed” can mean “to place seeds” or “to remove seeds”
- 解决模糊命名实体的链接问题:Paris → Paris, France vs. Paris Hilton vs. Paris, Texas, Hathaway → Berkshire Hathaway vs. Anne Hathaway
- window classfication
- 思想:在一个包含上下文词的窗口中对一个词进行分类
- 实现方案:将窗口中的词向量平均在进行分类,但这样会损失词的位置信息。
4.4 softmax窗口分类器
与简单的平均向量分类不同,可以训练一个softmax分类器来分类。
将窗口中的词向量首尾拼接,那么 x w i n d o w x_{window} xwindow可以看做一个向量:

y ^ = p ( y ∣ x ) = e x p ( w y ⋅ x ) ∑ c ∈ C e x p ( w c ⋅ x ) \hat y = p(y|x) = \frac{exp(w_y\cdot x)}{\sum_{c \in C}exp(w_c \cdot x)} y^=p(y∣x)=∑c∈Cexp(wc⋅x)exp(wy⋅x)
- 创建二分类器:对一个窗口中间词是否为NE(named entity)进行判断,我们需要使中间词为实体的窗口获得较高的分数。
对于一个三层神经网络使用激活函数a:
s c o r e ( x ) = U T a ∈ R s = s c o r e ( " m u e u m e s i n P a r i s a r e a m a z i n g " ) a = f ( z ) s = U T f ( W x + b ) score(x) = U^Ta \in R\\ s = score("mueumes in Paris are amazing") \\ a = f(z) \\ s = U^Tf(Wx+b) score(x)=UTa∈Rs=score("mueumesinParisareamazing")a=f(z)s=UTf(Wx+b)
加入词向量长度为4,窗口大小为5,实体类别数为8,那么 x ∈ R 20 × 1 , U ∈ R 8 × 1 , W ∈ R 8 × 20 x \in R^{20 \times 1}, U \in R^{8 \times 1}, W \in R^{8 \times 20} x∈R20×1,U∈R8×1,W∈R8×20
4.5 计算过程
来复习一下SGD:
θ n e w = θ o l d − α ∇ θ J ( θ ) \theta^{new} = \theta^{old} - \alpha \nabla_{\theta} J(\theta) θnew=θold−α∇θJ(θ)
如何计算 ∇ θ J ( θ ) \nabla_{\theta} J(\theta) ∇θJ(θ)? 1. 手写推导(上节课我们干过啦)2. 反向传播
手写梯度计算:(1)基本方法是多变量梯度推导。(2)更高效的方式是以向量为基本单位,进行矩阵运算。(课程笔记中包含更多的相关基础知识,Minning老师强调了几遍应该很重要)
五、梯度计算
5.1 1-output 和 n-input的函数(标量对向量求导)
f ( x ) = f ( x 1 , x 2 , ⋯ , x n ) ( 注 意 这 里 偏 导 的 维 度 和 自 变 量 维 度 一 致 ) ∂ f ∂ x = [ ∂ f ∂ x 1 , ∂ f ∂ x 2 , ⋯ , ∂ f ∂ x n ] f(\boldsymbol{x}) = f(x_1, x_2, \cdots, x_n) \\ (注意这里偏导的维度和自变量维度一致) \\ \frac{\partial f}{\partial \boldsymbol{x}} = \left[ \frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2}, \cdots, \frac{\partial f}{\partial x_n} \right] f(x)=f(x1,x2,⋯,xn)(注意这里偏导的维度和自变量维度一致)∂x∂f=[∂x1∂f,∂x2∂f,⋯,∂xn∂f]
5.2 m-outputs 和 n-inputs的函数(向量对向量求导)
f ( x ) = [ f 1 ( x 1 , x 2 , … , x n ) , … , f m ( x 1 , x 2 , … , x n ) ] f ( x ) = \left[ f _ { 1 } \left( x _ { 1 } , x _ { 2 } , \ldots , x _ { n } \right) , \ldots , f _ { m } \left( x _ { 1 } , x _ { 2 } , \ldots , x _ { n } \right) \right] f(x)=[f1(x1,x2,…,xn),…,fm(x1,x2,…,xn)]
求导结果就是jacobian矩阵:
∂ f ∂ x = [ ∂ f 1 ∂ x 1 ⋯ ∂ f 1 ∂ x n ⋮ ⋱ ⋮ ∂ f m ∂ x 1 ⋯ ∂ f m ∂ x n ] \frac { \partial \boldsymbol { f } } { \partial \boldsymbol { x } } = \left[ \begin{array} { c c c } { \frac { \partial f _ { 1 } } { \partial x _ { 1 } } } & { \cdots } & { \frac { \partial f _ { 1 } } { \partial x _ { n } } } \\ { \vdots } & { \ddots } & { \vdots } \\ { \frac { \partial f _ { m } } { \partial x _ { 1 } } } & { \cdots } & { \frac { \partial f _ { m } } { \partial x _ { n } } } \end{array} \right] \\ ∂x∂f=⎣⎢⎡∂x1∂f1⋮∂x1∂fm⋯⋱⋯∂xn∂f1⋮∂xn∂fm⎦⎥⎤
相当于
( ∂ f ∂ x ) i j = ∂ f i ∂ x j \left( \frac { \partial f } { \partial x } \right) _ { i j } = \frac { \partial f _ { i } } { \partial x _ { j } } (∂x∂f)ij=∂xj∂fi
注意这里每一行代表一个子函数对自变量求导的结果。
5.3 链式法则
只需要将复合函数每一层的jacobian矩阵相乘:
h = f ( z ) z = W x + b ∂ h ∂ x = ∂ h ∂ z ∂ z ∂ x = ⋯ \begin{array} { l } { h = f ( z ) } \\ { z = W x + b } \\ { \frac { \partial h } { \partial x } = \frac { \partial h } { \partial z } \frac { \partial z } { \partial x } = \cdots} \end{array} \\ h=f(z)z=Wx+b∂x∂h=∂z∂h∂x∂z=⋯
5.4 常用求导公式
- h = f ( z ) \boldsymbol{h} = f(\boldsymbol{z}) h=f(z),且 h i = f ( z i ) h_i = f(z_i) hi=f(zi), 那么雅克比矩阵为一个对角阵, 这个比较特殊且重要,因为这实际上就是神经网咯中的激活函数,由于是一个对角阵,在计算的时候就把对角线拿出来当向量用啦:
( ∂ h ∂ z ) i j = ∂ h i ∂ z j = ∂ ∂ z j f ( z i ) = { f ′ ( z i ) if i = j 0 if otherwise = [ f ′ ( z 1 ) ⋯ 0 ⋮ ⋱ ⋮ 0 ⋯ f ′ ( z n ) ] \begin{aligned} \left( \frac { \partial h } { \partial z } \right) _ { i j } & = \frac { \partial h _ { i } } { \partial z _ { j } } = \frac { \partial } { \partial z _ { j } } f \left( z _ { i } \right) \\& = \left\{ \begin{array} { l l } { f ^ { \prime } \left( z _ { i } \right) } & { \text { if } i = j } \\ { 0 } & { \text { if otherwise } } \end{array} \right.\\ & = \left[ \begin{matrix} f'(z_1) & \cdots & 0 \\ \vdots& \ddots &\vdots \\ 0 & \cdots &f'(z_n)\end{matrix} \right]\end{aligned} (∂z∂h)ij=∂zj∂hi=∂zj∂f(zi)={f′(zi)0 if i=j if otherwise =⎣⎢⎡f′(z1)⋮0⋯⋱⋯0⋮f′(zn)⎦⎥⎤ - 证明推导以下矩阵:
∂ ∂ x ( W x + b ) = W . ∂ ∂ b ( W x + b ) = I . ∂ ∂ u ( u T h ) = h T \begin{array} { l } { \frac { \partial } { \partial x } ( W x + b ) = W } \\ .\\{ \frac { \partial } { \partial b } ( W x + b ) = I } \\.\\ { \frac { \partial } { \partial u } \left( u ^ { T } h \right) = h ^ { T } } \end{array} ∂x∂(Wx+b)=W.∂b∂(Wx+b)=I.∂u∂(uTh)=hT
6. 反向传播(backpropagation)计算实例
对于如下这个简单的神经网络(其功能是对一个窗口给出一个逻辑回归评分),我们来通过反向传播计算参数梯度:
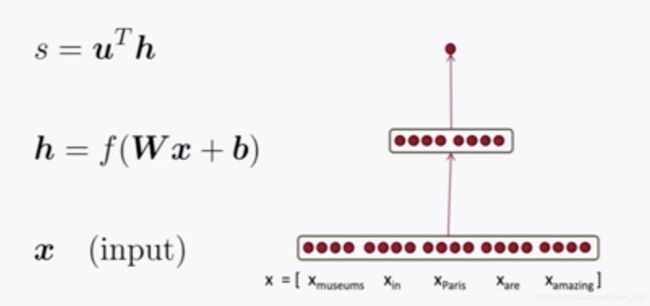
6.1 网络拆解
现将网络的每一个复合函数都拆分开,那么top-down的计算如下:
s = u T h s = u^Th s=uTh
h = f ( z ) h = f(z) h=f(z)
z = W x + b z = Wx+b z=Wx+b
x ⋯ ( i n p u t ) x \cdots (input) x⋯(input)
6.2 局部误差信号和局部输入信号
其中需要求导的参数为x, W, b, u。运用链式法则我们可以省略掉很多重复计算从而提高效率, 因为参数W, x, b都依赖前面两个复合函数:
∂ s ∂ b = ( ∂ s ∂ h ∂ h ∂ z ) ∂ z ∂ b \frac{\partial s}{\partial b} = \left(\frac{\partial s}{\partial h}\frac{\partial h}{\partial z}\right) \frac{\partial z}{\partial b} ∂b∂s=(∂h∂s∂z∂h)∂b∂z
∂ s ∂ W = ( ∂ s ∂ h ∂ h ∂ z ) ∂ z ∂ W \frac{\partial s}{\partial W} = \left( \frac{\partial s}{\partial h}\frac{\partial h}{\partial z}\right) \frac{\partial z} {\partial W} ∂W∂s=(∂h∂s∂z∂h)∂W∂z
∂ s ∂ x = ( ∂ s ∂ h ∂ h ∂ z ) ∂ z ∂ x \frac{\partial s}{\partial x} = \left(\frac{\partial s}{\partial h}\frac{\partial h}{\partial z}\right) \frac{\partial z}{\partial x} ∂x∂s=(∂h∂s∂z∂h)∂x∂z
这个公共部分通常按照如下表示,称为神经网络中的局部误差信号(local error signal), 这个名称很有意思, 把网络中的误差当做一个信号,从loss函数往输出层反向传播。这里的局部是指当前层。
δ = ∂ s ∂ h ∂ h ∂ z = h ∘ f ′ ( z ) 这 里 不 知 道 是 不 是 老 师 的 p p t 算 错 了 , 我 觉 得 应 该 是 u ∘ f ′ ( z ) \delta = \frac { \partial s } { \partial h } \frac { \partial h } { \partial z } = h \circ f ^ { \prime } ( z )\\ 这里不知道是不是老师的ppt算错了,我觉得应该是u \circ f ^ { \prime } ( z ) δ=∂h∂s∂z∂h=h∘f′(z)这里不知道是不是老师的ppt算错了,我觉得应该是u∘f′(z)
对于每一层参数,有局部误差信号、局部输入信号、权重W, 对W求偏导的维度如下:
∂ s ∂ W = δ x T [ n × m ] [ n × 1 ] [ 1 × m ] \begin{aligned} & \frac { \partial s } { \partial \boldsymbol { W } } = &\boldsymbol { \delta }&\boldsymbol { x } ^ { T } \\ &[ n \times m ] &[ n \times 1 ]& [ 1 \times m ] \end{aligned} ∂W∂s=[n×m]δ[n×1]xT[1×m]
这这个可以用来检查自己的工作,对于每一层的输入到输出, 相当于外积。
∂ s ∂ W = δ x T = [ δ 1 ⋮ δ n ] [ x 1 , … , x m ] = [ δ 1 x 1 … δ 1 x m ⋮ ⋱ ⋮ δ n x 1 … δ n x m ] \frac { \partial s } { \partial \boldsymbol { W } } = \boldsymbol { \delta }\boldsymbol { x } ^ { T } = \left[ \begin{array} { c } { \delta _ { 1 } } \\ { \vdots } \\ { \delta _ { n } } \end{array} \right] \left[ x _ { 1 } , \ldots , x _ { m } \right] = \left[ \begin{array} { c c c } { \delta _ { 1 } x _ { 1 } } & { \ldots } & { \delta _ { 1 } x _ { m } } \\ { \vdots } & { \ddots } & { \vdots } \\ { \delta _ { n } x _ { 1 } } & { \ldots } & { \delta _ { n } x _ { m } } \end{array} \right] ∂W∂s=δxT=⎣⎢⎡δ1⋮δn⎦⎥⎤[x1,…,xm]=⎣⎢⎡δ1x1⋮δnx1…⋱…δ1xm⋮δnxm⎦⎥⎤
