Java计算二进制数中1的个数

前言

逐位法

查表法

Brian Kernighan法

分治法

Hamming Weight法

Hamming Weight优化法

Hamming Weight乘法优化法

MIT HAKMEM 169算法

江峰求一算法

分治法总结

效率测试

后记

前言

        昨天学习全组合时，突然涉及到如何计算二进制中1的问题，我就直接使用的Integer.bitCount的方法进行计算，但打开源码后，突然忘记它的原理了，因此我就在网上搜索了相关资料，但发现它们大多数都是C或者C++实现，就算是Java实现的也只是只言片语，不成系统，所有我就有了总结了他们的想法。当时天真的认为这些算法可能就涉及点位操作，随着深入学习后，有些算法充分利用了数论的相关理论，数学真的无所不在呀！！！

逐位法

        老惯例，首先说说最简单的算法，核心思想就是逐位去判断是否为1，然后对其数量进行统计。代码如下：

public static int bitCount(int n){
    int count = 0;
    while(n != 0){
        count += n & 1;
        n >>>= 1;
    }
    return count;
}

        这个算法需要注意的就是无符号右移运算符的问题，如果使用的是右移运算符，处理负数时，会出现死循环。虽然C或者C++没有无符号右移这个操作符，但它们可以直接使用unsigned int实现此操作。我们在单元测试的时候一定注意正负数都要测试到，否则很容易出现问题。

查表法

        在逐位法中，我们是逐位进行计算，效率不是很高，如果我们能够一次计算多位中1的数量，那效率将成倍提升，如何实现呢？抛开二进制转换为十进制时利用了1这个信息，一般而言二进制的值和1的数量并没有直接关系，因此难点就在于如何建立二进制值和1的数量之间的关系。在数学中，想要建立两个不相干变量a和b的关系，一般我们都会找一个和两者都有关系的变量c，来间接确定a和b的关系。首先二进制的值和十进制值有关系，但是1的数量好像找不到它和其他的关系，因此该问题转换为十进制值和1的数量关系，即十进制值如何映射1的数量。在我们学过的数据结构中，涉及到映射的有Map(键值映射)和Array(下标和值映射)。具体选哪一个呢，其实针对这个问题，两者都可以，但是数组查询效率以及空间利用率都大于Map，因此我们选择使用数组来映射十进制值和1数量的关系，即二进制值和1数量的关系，其中二进制的值作为数组下标，1的数量作为数组中的值，这种处理方式也叫查表法。

        如果大家对Integer源码比较熟悉的话，里面就有一些查表法的操作，如DigitOnes和DigitTens。查表法是用空间换时间的典型代表，数组开得太大会占用内存空间，开的太小对效率的提升又太小，因此需要根据程序的实际需求来制定合适的方案。为了兼顾空间和效率，我选择开辟长度为256的数组来存储8位二进制中1的数量值。Talk is cheap，代码如下：

private static final int[] oneNumberTable ={
    0,1,1,2,1,2,2,3,1,2,2,3,2,3,3,4,1,2,2,3,2,3,3,4,2,3,3,4,3,4,4,5,
    1,2,2,3,2,3,3,4,2,3,3,4,3,4,4,5,2,3,3,4,3,4,4,5,3,4,4,5,4,5,5,6,
    1,2,2,3,2,3,3,4,2,3,3,4,3,4,4,5,2,3,3,4,3,4,4,5,3,4,4,5,4,5,5,6,
    2,3,3,4,3,4,4,5,3,4,4,5,4,5,5,6,3,4,4,5,4,5,5,6,4,5,5,6,5,6,6,7,
    1,2,2,3,2,3,3,4,2,3,3,4,3,4,4,5,2,3,3,4,3,4,4,5,3,4,4,5,4,5,5,6,
    2,3,3,4,3,4,4,5,3,4,4,5,4,5,5,6,3,4,4,5,4,5,5,6,4,5,5,6,5,6,6,7,
    2,3,3,4,3,4,4,5,3,4,4,5,4,5,5,6,3,4,4,5,4,5,5,6,4,5,5,6,5,6,6,7,
    3,4,4,5,4,5,5,6,4,5,5,6,5,6,6,7,4,5,5,6,5,6,6,7,5,6,6,7,6,7,7,8
};
public static int bitCount(int n){
    int count = 0;
    for (int i = 0; i < 32; i += 8){
        count += oneNumberTable[(n >> i) & 0xFF];
    }
    return count;
}

        虽然这方法看起来笨笨的，但如果使用得当，就能极大提升程序运行效率。

Brian Kernighan法

        在逐位法中，我们是逐位判断1，比如二进制为0b1000，就需要判断三次0一次1，如何一步到位直接判断第四位的1呢？我们知道 =  + 1，这个1刚好就是可以当做n+1位中1的数量，再利用x & (x - 1)将n位及以下的位全置0，这样我们每次的操作都能获取含1的位，提升了逐位法的效率。具体代码如下：

public static int bitCount(int n){
    int count = 0;
    while(n != 0){
        n = n & (n - 1);
        count++;
    }
    return count;
}

        如果n & (n - 1) = 0，则说明此时的n值并无含1的位，因此我们也可以用n & (n - 1) == 0来判断一个数是否是2的幂次方。

分治法

        前面的三种方法虽然看起来不同，但都是逐位法的变种，其思想都是逐个计算。对于归并排序肯定大家都不陌生，它就是将待排数组分为多块，然后排序多块，最后进行合并操作。那么对于32位的二进制，我们能不能也把它分成多块，然后计算每一块他们所含1的数量，最后将多块的1数量累加起来，进而得到二进制数中1的个数呢？要实现这种操作，就有二个问题需要解决，一是如何计算每一块中所含1的数量，二是如何合并已被计算的块。我在Brian Kernighan法提到过 =  + 1这个式子，如果我们要计算第n+1位二进制值的十进制值，其结果为a *  = a *  + a，其中a就是第n位二进制值，即0或1。对于0b1101，我们记其四位的二进制值分别为a、b、c、d。

        0b1101中第四位的二进制值：a = a *  - a *  - a *  - a * ；

        0b1101中第三位的二进制值：b = b *  - b *  - b * ；

        0b1101中第二位的二进制值：c = c *  - c * ；

        0b1101中第一位的二进制值：d = d * ；

        则：a + b + c + d = (a*+b*+c*+d*)-(a*+b*+c*)-(a*+b* )-a*。

               a + b + c + d =  0b1101 - 0b0110 - 0b0011 - 0b0001。

        转换为位操作，即：a + b + c + d =  0b1101 -  ((0b1101 >>> 1) & 0b0111)

                                                                              -  ((0b1101 >>> 2) & 0b0011)

                                                                              -  ((0b1101 >>> 3) & 0b0001)。

        其中红体数字是掩码，避免高数位对结果产生影响。掩码的选取必须和块数量对应，如果数据是32位，块长度为4，则掩码0b0111也必须变为扩大八倍，即0x77777777。

        有了上面的理论基础，则对于二位的情况，a + b = x - ((x >>> 1) & 0b01)

                                               对于三位的情况，a + b + c = x - ((x >>> 1)  & 0b011) - ((x >>> 2) & 0b001)

以此类推，我们可以仅仅通过减、移位和掩码操作，就能计算任意位数块中所含1的数量。这也就解决了第一个问题。

        前面我们已经计算了指定位数块中1的数量了，如何累加相邻两位数块，使其合并成两倍的位数块呢？其实只需要右移相应位数，再相加，利用两倍的位数掩码消除脏数据即可。比如对于二位数块0b1001，(0b1001 + (0b1001 >>> 2) ) & 0b0011 = 0b0011，其结果就是两位数块累加的结果。此时，第二个问题也被解决了。

        综合前面所述，我们完全可以使用分治法来计算二进制数中1的个数，其中还包含一些优化操作，也将在下面的具体算法中得以说明。

Hamming Weight法

        该方法的初始位数块长度为2，然后分治为4位数块，接着8位数块，以此类推，最终扩大到32位数块，其结果就是1的数量。如果大家完全理解我前面的分治法原理，其实可以直接写出相应代码。在学习该算法时，我还是看看了关于它的维基百科，放个传送门：Hamming weight，解释还是比较详细的。这些东西说起来比较抽象，还是代码中理解吧。

public static int bitCount(int n){
    n = (n & 0x55555555) + ((n >>> 1) & 0x55555555);
    n = (n & 0x33333333) + ((n >>> 2) & 0x33333333);
    n = (n & 0x0F0F0F0F) + ((n >>> 4) & 0x0F0F0F0F);
    n = (n & 0x00FF00FF) + ((n >>> 8) & 0x00FF00FF);
    n = (n & 0x0000FFFF) + ((n >>> 16) & 0x0000FFFF);
    return n;
}

上面的代码真的美得让人不知所措。我把上面几个十六进制的值转换成二进制字符串，如下所示

0x55555555 = 01010101010101010101010101010101
0x33333333 = 00110011001100110011001100110011
0x0F0F0F0F = 00001111000011110000111100001111
0x00FF00FF = 00000000111111110000000011111111
0x0000FFFF = 00000000000000001111111111111111

        看到这些数值的二进制值，就比较清晰了，因为它初始位数块长度为2，所以第一步就是解决a + b的问题，这也是第一行代码的作用，第二行代码分治为4位，第三行代码分治为8位，一直分治到32位即可。理解了分治法思想，上面的代码看起来是非常之简单的。

Hamming Weight优化法

        Hamming Weight法的第一步操作，虽然是实现a + b，但我在介绍分治法时是使用的减法，实际操作能节约一次与操作，其实后续还有很多地方需要优化，这里我们先给出优化后的代码，再详细说明优化的思路。

public static int bitCount(int n){
    n = n - ((n >>> 1) & 0x55555555);
    n = (n & 0x33333333) + ((n >>> 2) & 0x33333333);
    n = (n + (n >>> 4)) & 0x0F0F0F0F;
    n = n + (n >>> 8);
    n = n + (n >>> 16);
    return n & 0x3F;
}

        第一步优化(少了一次与操作)我们在前面已经解释了，此处就不在赘言。第二步没变化，因为现在的n = 8a + 4b + 2c + d，单纯的减操作不能把n转换为a + b + c + d，因此，这里就照旧。第三步，直接把两者相加，然后掩码操作，我们知道四位里面最多有4个1，记作0100，就算两个块里面都是4个1，加起来也就是1000，结果没有溢出块限制，所以就可以直接加，但前面两步相加后的结果超出了块范围，比如11 + 11 = 110，就超过了二位的限制范围，所以必须分开加，再将结果放到分治后的块里面，这样又少了一次与操作。第四步，结果没有进行掩码处理，我们知道掩码处理是防止块里面有“脏”数据，因为32位整型数据最多就32个1，即最大值为00100000，所以绝对要保证后六位的绝对正确。打个比方，相邻的四个位桶里面分别装着0100和0010的数据，相加以后为0110，此时两个桶共同的位数为00100110，如果此时不用掩码0x0F0F0F0F处理，那么八个位桶的数值就是00100110= 38，这个数据弄脏了第六位，因此需要用掩码剔除它，使计算结果为0110= 6。第四步是八位数块，其最大值就是00001000 = 8，就算两个一样数值的块相加，其结果是00001000 00010000，分治后的16位数块也能保证最后六位数据的绝对正确，所以就无需利用掩码剔除脏数据，节约了两次与操作。第五步也如第四步一般，又节约了两次与操作。最后再用六位掩码获取最后六位的数值即可。因此该算法相比上面的算法，少了5次与操作。Integer的bitCount方法就是采用的该算法。

Hamming Weight乘法优化法

        小学我们都学过乘法，也知道乘法交换律，即c * (a + b) = a * c + b * c，这里面的加号就隐含了能计算c各位之和的可能性，比如12 * (10 + 1) = 132，其中第二位的3就是12的个位和十位之和；121 * (100 + 10 + 1) = 13431，其中第三位的3就是121的个位、十位和百位之和，此时我们大胆推测，假设一个数字x有n位，则x * 的结果的第n位等于数字x所有位数值的累加和，但是这个推测有一些不足，比如198 * 111 = 21978，第三位的9 != 1 + 9 + 8，这是因为1 + 9 + 8 = 18 > 9，需要进位，且1 + 9 = 10 > 9也需要进位，它的进位值1也加到位数累加值上，这两种情况都会“污染”累加值，因此上面的推测若想合理，则还需要加一个限制条件：所有位数值的累加和不能大于9，即不能出现进位情况。

        既然十进制乘法能通过乘法来累加所有位数值，那么我们也能将其推广到二进制。首先保证所有位数累加值不能出现进位，32位的累加值最大为32 = 0b100000，因此我们必须用大于或等于6位的的位数块来保存所有位的累加值，为了计算的方便，位数块的大小M最好是2的幂次方，这样能保证计算的累加值在32位的最左边，然后通过无符号右移(32 - M)位就可以直接获取累加值。假设我们使用八位的位数块来计算所有位的累加值，则32位数据可以分为4个位数块，四个位数块的十六进制的值分别记作0x0a、0x0b、0x0c和0x0d，则相应的乘法操作如下所示：

                                                                     0a  0b  0c  0d

                                                                     01  01  01  01

                                                                                                             

                                                                     0a  0b  0c  0d

                                                               0a  0b  0c  0d

                                                         0a  0b  0c  0d

                                                   0a  0b  0c  0d

        红色部分是溢出的数据，蓝色部分相加正是四个位数块的累加值，其值通过无符号右移32 - 8 = 24位即可得到。该算法的详细思路也可以参考维基百科的Hamming weight。具体代码如下：

public static int bitCount(int n){
    n = n - ((n >>> 1) & 0x55555555);
    n = (n & 0x33333333) + ((n >>> 2) & 0x33333333);
    n = (n + (n >>> 4)) & 0x0F0F0F0F;
    return (n * 0x01010101) >>> 24; 
}

        该方法的优化需要CPU中基本运算部件乘法器的给力。如果CPU执行乘法操作指令比较慢的话，这样优化可能会适得其反。但一般来说不会这样，比如说AMD在两个时钟周期里就可以完成乘法运算。至于Java的bitCount为什么没有选这种，可能也有这方面的考虑吧。

MIT HAKMEM 169算法

        在前面累加所有位数值时，我们采用了直接累加法和利用乘法交换律的性质来实现累加，那么还有没有其他方法来实现数值累加呢？我们对于余数都不陌生，5 % 9 = 5， 12 % 9 = 3， 123 % 9 = 6，是不是发现了点啥了，此时我们大胆假设，任意十进制数值x对9求余都等于x各位数值之和。对不对呢？很可惜不对，因为789 % 9 = 6，但是这个6 = (7 + 8 + 9) % 6，突然感觉柳暗花明又一村，此时我们将假设改为：任意十进制数值x对9求余都等于x各位数值之和对9求余。如果x各位数值之和小于9，则初始的解设也对。此时我们几乎找不到反例，但这并不代表假设一定成立，要想假设成立仍需数学来证明其正确性。其中9 = 10 - 1，这里的10就是十进制的权，将假设转换为数学模型，其核心就是证明(a + b * ) ≡ (a + b) mod (m - 1)，其中(a + b) < m - 1，m > 2，m为进制的权，a、b、m、p均为正整数。

        在证明之前，我们要用到数论中的两个余数定理，如下所示：

(a + b) % c = ((a % c) + (b % c)) % c
(a * b) % c = ((a % c) * b) % c

         证明：假设(a + b * ) ≡ (a + b) mod (m - 1)成立，记 r = m - 1，则(a + b * ) ≡ (a + b) mod r成立。

                    此时 (a + b * ) % r = ((a % r) + (b * ) % r) % r

                     a + b < m - 1  a < r , b < r

                    上式 = (a + (b * ) % r) % r

                  又  m > 2，则 r = m - 1 > 1

                    (r + 1) % r = (((r + 1) % r ) * (r + 1))  % r = (r + 1)  % r = 1

                    (b * ) % r = (((r + 1) % r) * b ) % r = b % r = b

                   (a + (b * ) % r) % r = (a + b) % r = a + b

                   (a + b * ) ≡ (a + b) mod (m - 1)，假设成立，证毕。

        利用上面的结论(这结论是我无意间发现的，我也不知道数论书中的余数定理是否包含该结论，不管有没有，这结论都为后续的算法研究奠定了基础。)，我们也就能轻松证明( + 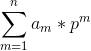) ≡ () 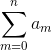mod (m - 1)，其中(a + b) < m - 1，m > 2，m为进制的权，、、...、、b、m、p均为正整数。因此我们推广前面的假设为，任意n进制的数值x对(n - 1)求余都等于x各位数值之和对(n - 1)求余。

        32位数值中各位值之和最大为32，因此，我们可以选择大于等于64(64是大于32的最小2的幂次方)的2的幂次方(选择2的幂次方，是为了与Hamming Weight法对应。)作为进制的权。根据前面的结论来实现计算二进制数中1的个数的操作。

        假设选取64位作为进制的权，则我们只需分治到6位数块，就可对(64 - 1) = 63求余来计算二进制数中1的个数。代码如下：

public static int bitCount(int n){
    n = n - (((n >>> 1) & 0xdb6db6db) + ((n >>> 2) & 0x49249249));
    n = (n + (n >>> 3)) & 0xc71c71c7;
    return n < 0 ? ((n >>> 30) + ((n << 2) >>> 2) % 63) : n % 63;
}

       代码中的三个掩码转换为二进制形式，如下所示：

0xdb6db6db = 11011011011011011011011011011011
0x49249249 = 01001001001001001001001001001001
0xc71c71c7 = 11000111000111000111000111000111

        第一行代码就是分治法中a + b + c的操作，第二行就是把三位数块分治成六位数块，因为负数求余也等于负数，且32 % 6 = 2，因此对于最终结果为负数的情况，先将前两位中1的数量直接通过移位计算出来，再把后面的30位中1的数量通过求余计算出来，两者相加即可得32位负数中1的数量。该算法也就是传说中的MIT HAKMEM 169算法。

江峰求一算法

        既然学透了MIT HAKMEM 169算法，那么我也来按照它的思路写个自己的版本，就叫做江峰求一算法，也证明了MIT HAKMEM 169算法并不是该思路的唯一算法。这里我选取256作为进制权数，分治到16位数块，再对255求余。具体代码如下：

public static int bitCount(int n){
    n = n - ((n >>> 1) & 0x55555555); 
    n = (n & 0x33333333) + ((n >>> 2) & 0x33333333); 
    n = (n + (n >>> 4)) & 0x0f0f0f0f; 
    n = (n + (n >>> 8)) & 0x00FF00FF;  
    return n % 255;
}

        这上面的几个十六进制值在原始Hamming Weight法里已经介绍过了，这里就不赘述了。前面四步来自于Hamming Weight优化法，主要是将位数块分治到16位数块。因为32 % 16 = 0，且数量32只保存在后六位中，所以不会出现负数情况，因此可以直接对(256 - 1) = 255求余，进而得到二进制数中1的个数。

        我在学习MIT HAKMEM 169算法时，网上很多博文都只是夸它一番，然后给出维基百科的代码，原理什么的并无涉及，连最基本的为什么要对63求余都没谈到，对一个自己一无所知的东西推崇备至，真的不是一个程序员应该做的事，所以为了调侃这行为，我就把该方法修改了一番，并用自己的名字进行命名。不管怎样，都希望自己能永远保持对未知的好奇，不人云亦云。

分治法总结

        根据前面的分析，分治法可以根据优化方式的不同，分化出非常多不同版本。接下来，我就简要总结一下这些优化方式的适用条件。

1. 按照分治法的理论推导，初始位数块的长度范围为2~32，理论上我们可以设计31种不同版本的分治法，但是随着长度的逐渐提高，构建a + b + c + ... + n所需要操作数也将成倍提高，具体操作数为1次减法、2 * n次与和2 * n次无符号右移。因此初始化位数块的长度不能太大，一般是选择2，又因为32只需要6位存储，所以也可以选3。
2. 利用乘法交换律能累加所有位数值，32只需要6位存储且为了保证计算的累加值在32位的最左边，一般初始块长度为2的幂次方。如果分治后位数块的长度大于等于6，就可以利用乘法加移位来计算二进制数中1的个数。
3. 利用余数性质也能累加所有位数值，我们只要保证分治后位数块长度大于6，计算结果在指定区间不溢出，即可使用余数定理进行优化。

效率测试

        因为逐位法和Brian Kernighan法效率较低，因此测试数据为-1000000到1000000，其余都是Integer.MIN_VALUE到Integer.MAX_VALUE。测试结果如下：

$ java -version
java version "1.8.0_111"  
Java(TM) SE Runtime Environment (build 1.8.0_111-b14)  
Java HotSpot(TM) 64-Bit Server VM (build 25.111-b14, mixed mode) 
$ The data range is from -1000000 to 1000000 .
逐位法：42ms
Brian Kernighan法：27ms
$ The data range is from -2147483648 to 2147483647.
查表法：6ms
Hamming Weight法：5ms
Hamming Weight优化法：4ms
Hamming Weight乘法优化法：4ms
MIT HAKMEM 169算法：1686ms
江峰求一算法：4ms

        运行结果和我预期差不多，分治法的效率非常之高，查表法也是隐藏的大黑马，MIT HAKMEM 169算法在负数处理上稍逊一筹，但处理正数的效率，和其它几个分治法几乎没区别，效率杠杠的。

后记

        总算写完了，刚开始学这部分时，还觉得好麻烦，怎么这么多稀奇古怪的操作，最后学完了，觉得也还好，只要知道算法原理，代码的编写也就自然而然了。不过能独立想到这些方法其实还是很难的，必须要对数学的累加求和有足够的认识，这次的算法学习也让我再次体会到数学的强大！

        差点忘了，这些方法的总结主要参考了这篇博文，放个传送门：求二进制数中1的个数 (上)，求二进制数中1的个数 (下)。这两篇2010年的博客，现在看来依旧具有极高的参考价值，值得我去学习，希望我也能如他般优秀。