浅谈IM软件业务知识——非对称加密,RSA算法,数字签名,公钥,私钥
----------------------------------------------------欢迎查看IM软件业务知识《专栏》-------------------------------------------------------------------
使用状态机来保持在线状态 【点击】 拼图算法,将零碎小图,整理到一张大图上【点击】
登录导航 【点击】 会话session的概念【点击】
“假在线’ 【点击】 非对称加密,RSA算法【点击】
如何建立安全socket连接、登录 【点击】 浅谈断线重连、心跳和长在线 【点击】
iOS 客户端创建网络连接,常见错误汇总 【点击】 protocolBuf 在iOS上的使用入门、讲解、指南 【点击】
实现富文本解析【点击】 UITableview Deceleration 加速滑动(惯性滑动)、弹性回归原理【点击】
--------------------------------------------------------------------------------------------------------------------------------------------------------------------
概述
首先了解一下相关概念:RSA算法:1977年由Ron Rivest、Adi Shamirh和LenAdleman发明的,RSA就是取自他们三个人的名字。算法基于一个数论:将两个大素数相乘非常容易,但要对这个乘积的结果进行 因式分解却非常困难,因此可以把乘积公开作为公钥,该算法能够抵抗目前已知的所有密码攻击。RSA算法是一种非对称算法,算法需要一对密钥,使用其中一个 加密,需要使用另外一个才能解密。我们在进行RSA加密通讯时,就把公钥放在客户端,私钥留在服务器。
RSA非对称加密算法,可以验证客户端和服务器双方的合法性,安全级别非常高!
这是目前地球上最重要的加密算法
如何生成公钥和私钥
1. 选择两个素数p=17,q=11
2. 计算乘机n = 17*11 = 187
3. 对n计算欧拉函数φ(n)=(p-1)(q-1) = 160。
4. 选择e,使得e与φ(n)互素且小于φ(n)。选择e=7 (实际应用中n是一个极大数,通常使用65537)
5. 计算d,使得de mod 160=1且d < 160.正确的值是23,这是因为23*7 = 161 = 10*16+1
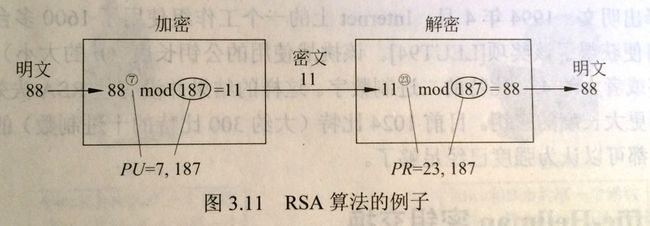
这样就得出了公钥PU={7,187} 私钥PR={23,187} 参考这里
如何加密、解密?
对于某一明文M和密文C,加密和解密有如下形式:加密:C=Me mod n
解密:M=Cd mod n = (Me)d mod n = Med mod n
如果,公钥PU=(7,187) 即(e,n)私钥PR=(23),187 即(d,n),带入公式如下图所示:
对于加密,需要计算C = 887 mod 187。利用模运算的性质,计算如下:
887mod187 = [(884 mod 187)*(882 mod 187)*(881mod)] mod 187
881 mod 187 = 88
882 mod 187 = 7744 mod 187 = 77
884 mod 187 = 59969536 mod 187 = 132
887mod187 = (88*77*132)mod 187 = 894432 mod 187 = 11
对于解密,计算M = 1123 mod 187 ;
M = 1123 mod 187 = [(111 mod 187)*(112 mod 187)*(114 mod 187)*(118 mod 187)*(118 mod 187)] mod 187
111 mod 187 = 11
112 mod 187 = 121
114 mod 187 = 14641 mod 187 = 55
118 mod 187 = 214 258 881 mod 187 = 33
M = 1123 mod 187 =(11*121*55*33*33)mod 187 = 79720245 mod 187 = 88
RSA的可靠性
回顾上面的密钥生成步骤,一共出现六个数字:
p
q
n
φ(n)
e
d
这六个数字之中,公钥用到了两个(n和e),其余四个数字都是不公开的。其中最关键的是d,因为n和d组成了私钥,一旦d泄漏,就等于私钥泄漏。
那么,有无可能在已知n和e的情况下,推导出d?
(1)ed≡1 (mod φ(n))。只有知道e和φ(n),才能算出d。
(2)φ(n)=(p-1)(q-1)。只有知道p和q,才能算出φ(n)。
(3)n=pq。只有将n因数分解,才能算出p和q。
结论:如果n可以被因数分解,d就可以算出,也就意味着私钥被破解。
可是,大整数的因数分解,是一件非常困难的事情。目前,除了暴力破解,还没有发现别的有效方法。维基百科这样写道:
"对极大整数做因数分解的难度决定了RSA算法的可靠性。换言之,对一极大整数做因数分解愈困难,RSA算法愈可靠。
假如有人找到一种快速因数分解的算法,那么RSA的可靠性就会极度下降。但找到这样的算法的可能性是非常小的。今天只有短的RSA密钥才可能被暴力破解。到2008年为止,世界上还没有任何可靠的攻击RSA算法的方式。
只要密钥长度足够长,用RSA加密的信息实际上是不能被解破的。"
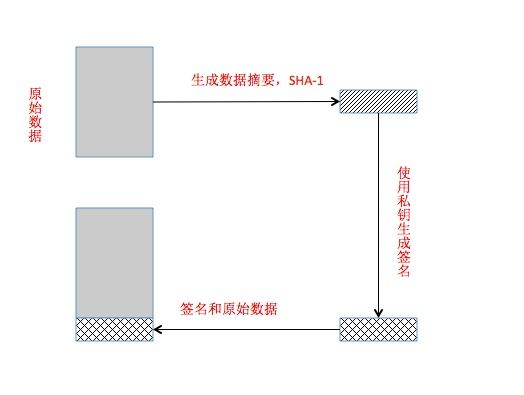
数字签名,私钥加密,公钥解密
2. 对摘要进行DER数据编码
3. RSA私钥加密
4. 字节串到位串的转换。
对于RSA算法,用任何一方密钥加密都可以用另外一个密钥解密;这也从另外一个角度说明,其实公钥和私钥是相对而言的,发放其中一个密钥出去,另外一个自然也就成为私钥了。
非对称加密案例
iOS平台RSA介绍
我们常见的证书可以看做是公钥,证书中包含了公钥和一些其他信息。IOS客户端的加解密,首先我们需要导入Security.framework,在iOS中,我们主要关注四个函数。
SecKeyEncrypt:使用公钥对数据进行加密。
SecKeyDecrypt:使用私钥对数据进行解密。
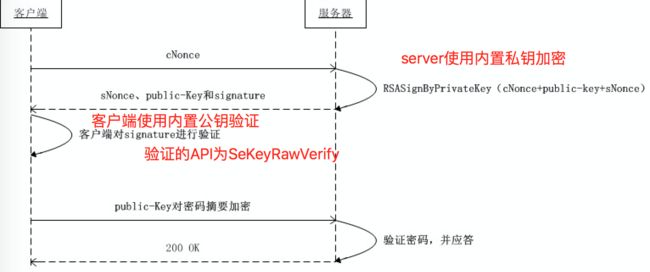
SecKeyRawVerify:使用公钥对数字签名和数据进行验证,以确认该数据的来源合法性。
SecKeyRawSign:使用私钥对数据进行摘要并生成数字签名。
从这几个函数中,我们可以看到,公钥能做的事情就有两个:加密数据,以及对服务器端发来的数据进行签名认证,但是如果你想跟我之前想的一 样,要使用公钥来对数据进行解密,那就没有自带API了。如果想在服务器端使用私钥加密数据,然后再在客户端使用公钥进行解密,以图这样来对交互数据进行加密,看来是行不通的。其实也应该是这样,公钥是公开的。同时,RSA因为都是做大数的运算,算法性能上比较差,如果做大数据量的加解密,对IOS来讲,肯定也是不合适的。
银行U盾
U盾的工作过程:当网银响应用户操作,将所有的指令信息打包,并通过USB口送入U盾,U盾在其内部由MPU使用证书(私钥)进行签名,然后送出。再由IE通过SSL传送到服务器。服务器收到指令包后由用户留存在密钥分发服务器上的公钥进行签名认证,若认证无误则执行指令。
隐患一
隐患二
最后
破解RSA被认为是所有计算机科学中最难的课题之一。因此,如果你发明了一种能够快速地将一个极大的数字分解为质数的方法,就不仅仅能够入侵瑞士银行的账户系统,而且还可以获得图灵奖了!