最优化方法——最速下降法,阻尼牛顿法,共轭梯度法
最优化方法——最速下降法,阻尼牛顿法,共轭梯度法
目录
最优化方法——最速下降法,阻尼牛顿法,共轭梯度法
1、不精确一维搜素
1.1 Wolfe-Powell 准则
2、不精确一维搜索算法计算步骤
3、最速下降法
3.1 基本思想
3.2 计算步骤
3.3 迭代过程
3.4 优缺点分析
4、(阻尼)牛顿法
4.1 基本思想
4.2 迭代过程
5、共轭方向法和共轭梯度法
5.1 共轭梯度法与前两种方法的比较
5.2 共轭梯度法的迭代过程
6、Python代码实现
7、迭代图像
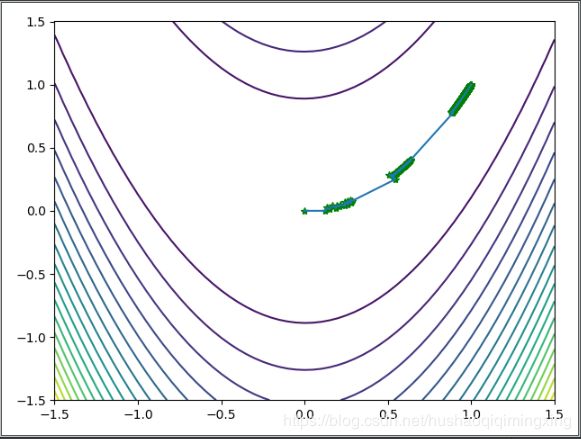
7.1 最速下降法迭代图像
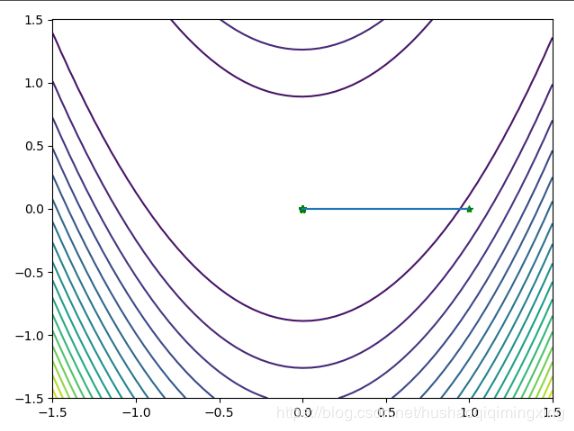
7.2 牛顿法迭代图像
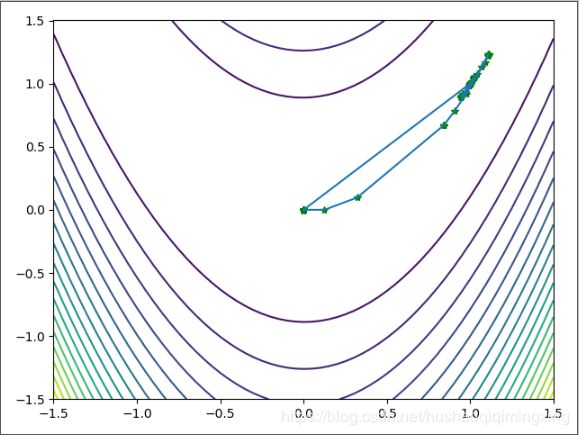
7.3 阻尼牛顿法迭代图像
7.4 共轭梯度法迭代图像
1、不精确一维搜素
1.1 Wolfe-Powell 准则
2、不精确一维搜索算法计算步骤
3、最速下降法
3.1 基本思想
3.2 计算步骤
3.3 迭代过程
3.4 优缺点分析
4、(阻尼)牛顿法
4.1 基本思想
4.2 迭代过程
5、共轭方向法和共轭梯度法
5.1 共轭梯度法与前两种方法的比较
5.2 共轭梯度法的迭代过程
6、Python代码实现
'''
wolfe powell 不精确一维搜索准则
1、f(x_(k)) - f(x_(k+1)) >= -c_1 * lamda * inv(g_k) * s_(k)
2、inv(g_(k+1)) * s_(k) >= c_2 * inv(g_(k)) * s_(k)
根据计算经验,常取c_1 = 0.1, c_2 = 0.5
0 < c_1 < c_2 < 1
'''
"""
函数 f(x)=100*(x(1)^2-x(2))^2+(x(1)-1)^2
梯度 g(x)=(400*(x(1)^2-x(2))*x(1)+2*(1-x(1)),-200*(x(1)^2-x(2)))
"""
import numpy as np
import sys
import matplotlib.pyplot as plt
def object_function(xk):
f = 100 * (xk[0] ** 2 - xk[1]) ** 2 + (xk[0] - 1) ** 2
return f
def gradient_function(xk):
gk = np.array([
400 * (xk[0] ** 2 - xk[1]) * xk[0] + 2 * (xk[0] - 1),
-200 * (xk[0] ** 2 - xk[1])
])
return gk
def hesse(xk):
# h = np.zeros(2, 2)
h = np.array([
[2 + 400 * (3 * xk[0] ** 2 - xk[1]), -400 * xk[0]],
[-400 * xk[0], 200]
])
return h
def wolfe_powell(xk, sk):
alpha = 1.0
a = 0.0
b = -sys.maxsize
c_1 = 0.1
c_2 = 0.5
k = 0
while k < 100:
k += 1
if object_function(xk) - object_function(xk + alpha * sk) >= -c_1 * alpha * np.dot(gradient_function(xk), sk):
#print('满足条件1')
if np.dot(gradient_function(xk + alpha * sk), sk) >= c_2 * np.dot(gradient_function(xk), sk):
#print('满足条件2')
return alpha
else:
a = alpha
alpha = min(2 * alpha, (alpha + b) / 2)
else:
b = alpha
alpha = 0.5 * (alpha + a)
return alpha
# 最速下降法
def steepest(x0, eps):
gk = gradient_function(x0)
sigma = np.linalg.norm(gk)
step = 0
xk = x0
w = np.zeros((2, 10 ** 4))# 保存迭代把变量xk
sk = -1 * gk
while sigma > eps and step < 10000:
alpha = wolfe_powell(xk, sk)
w[:, step] = np.transpose(xk)
step += 1
xk += alpha * sk
gk = gradient_function(xk)
sk = -1 * gk
sigma = np.linalg.norm(gk)
#print(gk,sigma)
print('--The {}-th iter, the result is {},object value is {:.4f}'.format(step, np.array(xk), object_function(xk)))
return w
# newton法
def newton(x0, eps):
step = 0
xk = x0
gk = gradient_function(xk)
hessen = hesse(xk)
sigma = np.linalg.norm(gk)
sk = -1 * np.dot(np.linalg.inv(hessen), gk)
w = np.zeros((2, 10 ** 3))# 保存迭代把变量xk
while sigma > eps and step < 100:
# newton 法中alpha = 1
w[:, step] = np.transpose(xk)
step += 1
xk = xk + sk
gk = gradient_function(xk)
hessen = hesse(xk)
sigma = np.linalg.norm(gk)
sk = -1 * np.dot(np.linalg.inv(hessen), gk)
print('--The {}-th iter, the result is {},object value is {:.4f}'.format(step, np.array(xk), object_function(xk)))
return w
# 阻尼 newton法
def Damped_newton(x0, eps):
step = 0
xk = x0
gk = gradient_function(xk)
hessen = hesse(xk)
sigma = np.linalg.norm(gk)
sk = -1 * np.dot(np.linalg.inv(hessen), gk)
w = np.zeros((2, 10 ** 3))# 保存迭代把变量xk
while sigma > eps and step < 100:
alpha = wolfe_powell(xk, sk)
w[:, step] = np.transpose(xk)
step += 1
xk = xk + alpha * sk
gk = gradient_function(xk)
hessen = hesse(xk)
sigma = np.linalg.norm(gk)
sk = -1 * np.dot(np.linalg.inv(hessen), gk)
print('--The {}-th iter, the result is {},object value is {:.4f}'.format(step, np.array(xk), object_function(xk)))
return w
# 共轭梯度法
def conjugate_gradient(x0, eps):
xk = x0
gk = gradient_function(xk)
sigma = np.linalg.norm(gk)
sk = -gk
step = 0
w = np.zeros((2, 10 ** 3))# 保存迭代把变量xk
while sigma > eps and step < 1000:
w[:, step] = np.transpose(xk)
step += 1
alpha = wolfe_powell(xk, sk)
xk = xk + alpha * sk
g0 = gk
gk = gradient_function(xk)
miu = (np.linalg.norm(gk) / np.linalg.norm(g0))**2
sk = -1 * gk + miu * sk
sigma = np.linalg.norm(gk)
print('--The {}-th iter, the result is {},object value is {:.4f}'.format(step, np.array(xk),object_function(xk)))
return w
if __name__ == '__main__':
eps = 1e-5
x0 = np.array([0.0, 0.0])
# 最速下降法
W = steepest(x0, eps)
# Newton迭代法
# W = newton(x0,eps)
# 阻尼Newton法
# W = Damped_newton(x0, eps)
# 共轭梯度算法
# W = conjugate_gradient(x0, eps)
# 画出目标函数图像
X1 = np.arange(-1.5, 1.5 + 0.05, 0.05)
X2 = np.arange(-1.5, 1.5 + 0.05, 0.05)
[x1, x2] = np.meshgrid(X1, X2)
f = 100 * (x1 ** 2 - x2) ** 2 + (x1 - 1) ** 2 # 给定的函数
plt.contour(x1, x2, f, 20) # 画出函数的20条轮廓线
plt.plot(W[0, :], W[1, :], 'g*', W[0, :], W[1, :]) # 画出迭代点收敛的轨迹
plt.show()
7、迭代图像
7.1 最速下降法迭代图像
7.2 牛顿法迭代图像
7.3 阻尼牛顿法迭代图像
7.4 共轭梯度法迭代图像