基于meta-path的异质网络Embedding-HIN2vec

HIN2vec 主要是学习异质网络节点和关系的embedding向量表示。HIN2vec主要跟为训练数据准备和表示学习两部分。在训练数据准备中，将网络数据表示成 <x,y,r,L(x,y,r)> 的形式，它堆不同的关系类型 r 加以区分；在表示学习中，主要实现方式是最大化多个联合（jointly）二分类的概率（预测将relation的类别：即两个节点之间是否存在某种指定的meta-path: π ）联合训练。模型框架如下图所示：

• 表示学习
  在给定异质网络 G=(V,E,Φ,Ψ) 时，meta-path π 表示的是节点类型序列 a1,a2,⋯,an 和/或 边类型的序列 r1,r2,⋯,rn−1
  
  π=a1⟶r1a2⟶r2⋯⟶rn−1an

如途中是一个paper-author的异质网络，P代表论文节点， A代表作者节点，在2-hops范围内的meta-path可以有：

R={P−P,P−A,A−P,P−P−A,P−P−P,P−A−P,A−P−P,A−P−A}

第一种模型把预测节点对(x,y)之间的关系类型表示为多分类问题 P(ri|x,y)(i=1,⋯,|R|) 。

如图所示，输入层为两个长度为|V|的 one-hot 向量 x⃗ ,y⃗  ，经过转换变为d维度的隐含层向量 WTxx⃗ ,WTyy⃗  。其中， Wx,Wy 是 |V|×d 的矩阵，这两个矩阵可以相同也可以不相同（区分两个节点在关系中的角色），在论文的实验中设置为同一个矩阵。在输出层则为一个维度为|R|的向量，每一个item表示节点x,y之间存在该关系的可能性。 WR 是一个维度为 d×|R| 的矩阵。这种方法有一个很明显的缺陷，对于每一个节点对在准备训练数据时都要遍历整个网络来找寻所有可能的关系类型r。而且，无论节点对之间是否存在关系类型r，转换矩阵 Wx,Wy,WR 在训练时对于多有的关系类型r都要更新。因而，论文中提出了HIN2vec的方法。

• HIN2vec
  这个模型将上述的多分类问题变为多个二分类问题。模型框架如下图所示：

输入层：关系类型不再作为预测对象，而是作为输入出现在输入层，二分类要预测的是节点 x,y 之间是否存在关系r。输入向量 r⃗  的维度是|R|。与节点的转换矩阵不同，关系的转换矩阵 WR 有一个正则化函数 f01(⋅) ，得到的隐含层的向量为 f01(WTR⋅r⃗ ) 。

隐含层： 输入为 WTxx⃗ ,WTyy⃗ ,f01(WTRr⃗ ) ，输出为 WTxx⃗ ⊙WTyy⃗ ⊙f01(WTRr⃗ )
关于 ⊙ 运算在实验中作者分别采用了Hadamard、均值、差，差的绝对值四种，最后Hadamard函数的效果最好。

输出层： 输入为 ∑WTxx⃗ ⊙WTyy⃗ ⊙f01(WTRr⃗ ) ， 也就是对隐含层的d维向量的元素求和。激活函数为sigmoid函数。

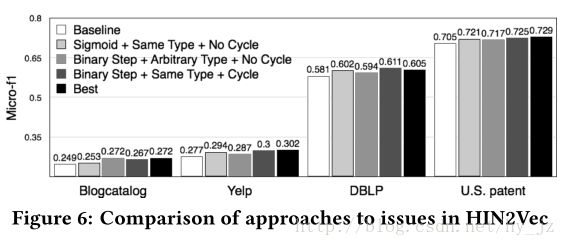
正则函数本文采用的是 Binary Step 函数（论文实验证明比sigmoid函数好些），加这个正则函数，一个是避免 WR 中的负值影响节点向量的符号；一个是避免 WR 中的值边的太大，影响训练效果。

• 优化目标函数
  HIN2vec模型，训练数据集D的形式为 <x,y,r,L(x,y,r)> ，其中 L(⋅) 是二元值，表示节点x,y之间是否存在关系r。目标函数具体为：
  
  O∝logO=∑x,y,r∈DlogOx,y,r(x,y,r)
  
  其中 logOx,y,r(x,y,r) 衡量的是HIN2vec如何正确预测训练数据。
  
  Ox,y,r(x,y,r)={P(r|x,y),ifL(x,y,r)=11−P(r|x,y),ifL(x,y,r)=0

log概率为：

logOx,y,r(x,y,r)=L(x,y,r)logP(r|x,y)+[1−L(x,y,r)]log[1−P(r|x,y)]

节点x,y之间存在关系r时，概率P(r|x,y)为：

P(r|x,y)=sigmoid(∑WTxx⃗ ⊙WTyy⃗ ⊙f01(WTRR⃗ ))

• 训练数据的准备
  两点，一个是在构建负样本的时候，只是随机替换(x,y,r)中节点x或者节点y,并且节点 x′ 或者节点 y′ 与节点x， 节点y是同一个节点类型；另一个是在random walk的时候去掉环cycles，比如 (A1,A1,A−P−A) 这种样本是没有意义的。

• 实验
  论文的实验还是很充分的。用了四个数据集：Blogcatalog 、Yelp、DBLP、U.S. Patent。实验主要是链路预测。但是论文对实验中的参数都做了充分的实验。如下图所示的对训练数据准备中使用的几种优化方案分别做了对比：