用机器学习解决问题的思路
原始博客: 机器学习系列(4)_机器学习算法一览,应用建议与解决思路
当我们拿到一堆数据时,该如何去下手?
1. 首先要可视化,了解数据
2. 选择合适的机器学习算法
3. 分析所得模型的状态(过拟合、欠拟合)并解决
4. 大量级数据的特征分析和可视化
5. 各种损失函数的优缺点及选择
1 数据可视化

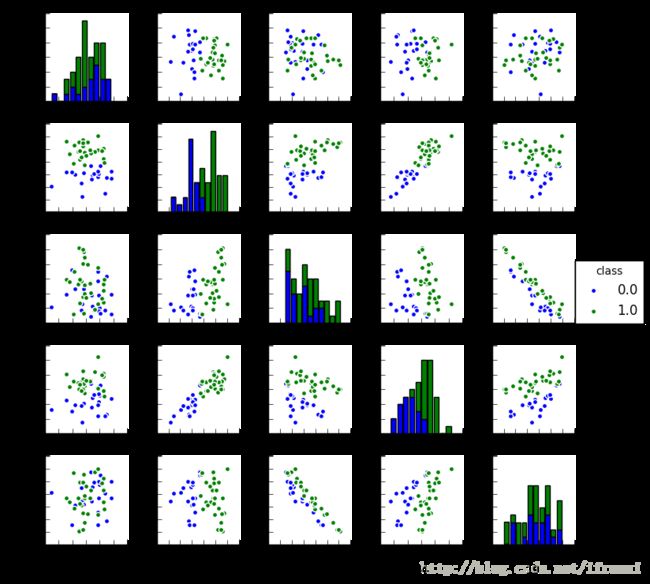
然而当大量数据出现的时候,图像可视化就可以让我们直观的理解数据的分布和特性,比如 散列分布图和柱状图。 python中可视化包: matplotlib 或者 Seaborn等。
安装:
pip install 包名从上图可以看出:
第11维和第14维在一起可以很好的区分数据,类似的还有8和11、11和12等。而12和19则具有很强的负相关性。
下面计算各维度特征之间(以及最后的类别)的相关性,来验证上面的结论。
最新版的seaborn中取消了corrplot,代替为heatmap,官方示例:
Plotting a diagonal correlation matrix
可以看到第11维特征和第14维特征和类别有极强的相关性(颜色很浅),同时它们俩之间也有极高的相关性。而第12维特征和第19维特征却呈现出极强的负相关性(颜色很深)。
强相关的特征其实包含了一些冗余的特征,而除掉上图中颜色较深的特征,其余特征包含的信息量就没有这么大了,它们和最后的类别相关度不高,甚至各自之间也没什么先惯性。
对于大量级数据处理,后面会介绍到。
2 机器学习算法选择
Ng说过做机器学习,先尝试做出一个baseline然后再去尝试改进。
根据机器学习图谱:

选择使用LinearSVC(线性核SVM分类)。
原作者自己写了一个函数,用来画学习曲线,调用也很简单。该函数可以画出训练集和测试集的精确度和方差情况。
#绘制学习曲线,以确定模型的状况
def plot_learning_curve(estimator, title, X, y, ylim=None, cv=None,train_sizes=np.linspace(.1, 1.0, 5)):
"""
画出data在某模型上的learning curve.
参数解释
----------
estimator : 你用的分类器。
title : 表格的标题。
X : 输入的feature,numpy类型
y : 输入的target vector
ylim : tuple格式的(ymin, ymax), 设定图像中纵坐标的最低点和最高点
cv : 做cross-validation的时候,数据分成的份数,其中一份作为cv集,其余n-1份作为training(默认为3份)
"""
plt.figure()
train_sizes, train_scores, test_scores = learning_curve(
estimator, X, y, cv=5, n_jobs=1, train_sizes=train_sizes)
train_scores_mean = np.mean(train_scores, axis=1)
train_scores_std = np.std(train_scores, axis=1)
test_scores_mean = np.mean(test_scores, axis=1)
test_scores_std = np.std(test_scores, axis=1)
plt.fill_between(train_sizes, train_scores_mean - train_scores_std,
train_scores_mean + train_scores_std, alpha=0.1,
color="r")
plt.fill_between(train_sizes, test_scores_mean - test_scores_std,
test_scores_mean + test_scores_std, alpha=0.1, color="g")
plt.plot(train_sizes, train_scores_mean, 'o-', color="r",
label="Training score")
plt.plot(train_sizes, test_scores_mean, 'o-', color="g",
label="Cross-validation score")
plt.xlabel("Training examples")
plt.ylabel("Score")
plt.legend(loc="best")
plt.grid("on")
if ylim:
plt.ylim(ylim)
plt.title(title)
plt.show()使用svc的结果:
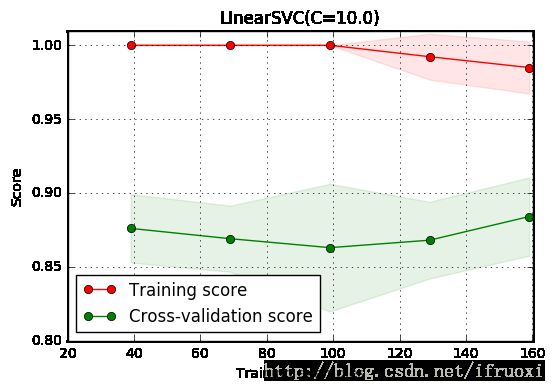
从图中可以看出:随着样本数的增加训练score下降,交叉验证得分上升,并且两者差距很大,训练集上的识别率远高于测试集,说明模型处于过拟合状态。
3 过拟合的解决
有几种方法可以处理:
1 增加样本量,(相当于给出更多的练习题目,不让他们去死记硬背所有的答案)
2 减少特征的量(简化了模型,降低了方差,提高了偏差)
从另外一个角度看,我们之所以做特征选择,是想降低模型的复杂度,而更不容易刻画到噪声数据的分布。从这个角度出发,我们还可以有
(1)多项式你和模型中降低多项式次数
(2)神经网络中减少神经网络的层数和每层的结点数
(3)SVM中增加RBF-kernel的bandwidth等方式来降低模型的复杂度。
3 增强正则化参数(最有效的办法)
寻找最优的参数可以在在交叉验证集上做grid-search查找最好的正则化系数(对于大数据样本,我们依旧需要考虑时间问题,这个过程可能会比较慢)。
在自动选择特征中有一个小技巧:
1: l2正则化,它对于最后的特征权重的影响是,尽量打散权重到每个特征维度上,不让权重集中在某些维度上,出现权重特别高的特征。
2: l1正则化,它对于最后的特征权重的影响是,让特征获得的权重稀疏化,也就是对结果影响不那么大的特征,干脆就拿不着权重。
对于欠拟合解决:
1 调整你的特征(找更有效的特征!!, 高维特征)
2 使用更复杂一点的模型(比如说用非线性的核函数)
4 关于大数据样本集和高维特征空间
对于大量的数据而言,我们用LinearSVC可能就会有点慢了,我们注意到机器学习算法使用图谱推荐我们使用SGDClassifier。
其实本质上说,这个模型也是一个线性核函数的模型,不同的地方是,它使用了随机梯度下降做训练,所以每次并没有使用全部的样本,收敛速度会快很多。再多提一点,SGDClassifier对于特征的幅度非常敏感,也就是说,我们在把数据灌给它之前,应该先对特征做幅度调整,当然,用sklearn的StandardScaler可以很方便地完成这一点。
SGDClassifier每次只使用一部分(mini-batch)做训练,在这种情况下,我们使用交叉验证(cross-validation)并不是很合适,我们会使用相对应的progressive validation:简单解释一下,estimator每次只会拿下一个待训练batch在本次做评估,然后训练完之后,再在这个batch上做一次评估,看看是否有优化
对于大数据下的可视化
首先需要的是降维。具体的过程参考原文,原文已经介绍的几种方法都非常有效
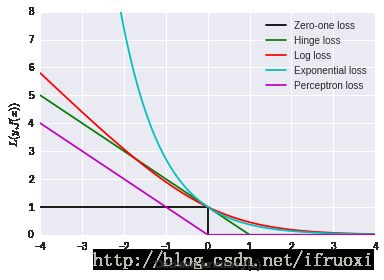
损失函数的对比
0-1损失函数(zero-one loss)非常好理解,直接对应分类问题中判断错的个数。但是比较尴尬的是它是一个非凸函数,这意味着其实不是那么实用。
hinge loss(SVM中使用到的)的健壮性相对较高(对于异常点/噪声不敏感)。但是它没有那么好的概率解释。
log损失函数(log-loss)的结果能非常好地表征概率分布。因此在很多场景,尤其是多分类场景下,如果我们需要知道结果属于每个类别的置信度,那这个损失函数很适合。缺点是它的健壮性没有那么强,相对hinge loss会对噪声敏感一些。
多项式损失函数(exponential loss)(AdaBoost中用到的)对离群点/噪声非常非常敏感。但是它的形式对于boosting算法简单而有效。
感知损失(perceptron loss)可以看做是hinge loss的一个变种。hinge loss对于判定边界附近的点(正确端)惩罚力度很高。而perceptron loss,只要样本的判定类别结果是正确的,它就是满意的,而不管其离判定边界的距离。优点是比hinge loss简单,缺点是因为不是max-margin boundary,所以得到模型的泛化能力没有hinge loss强。