最短路算法（Floyd，Dijkstra，.Bellman-Ford）

最近复习了下最短路，顺便写篇博客加强下自己的印象

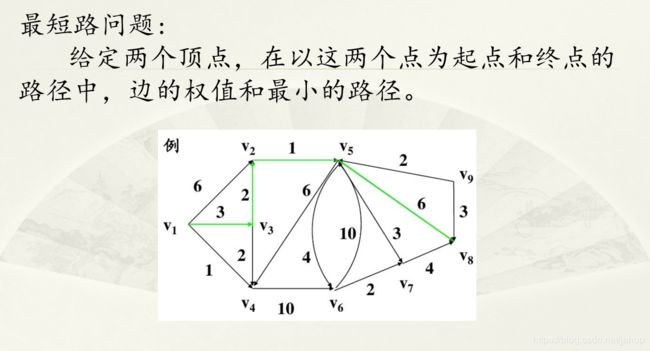
1.Floyd算法
我认为是最短路最简单的算法，但一般来说简单的都不是什么好东西，因为复杂度比较高；

*核心思想：
要缩短两点之间的距离，就需要第三个顶点来松弛。

*具体步骤：
依次用1到n号顶点做中转，松弛任意两点之间的距离。

因为这个算法比较简单，就直接上代码了；

#include


using namespace std;

const int N=2000;
int main()
{
    
    int maps[N][N];
    for(int i=1;i<=N;i++)
        for(int j=1;j<=N;j++)
        {if(i==j)
            maps[i][j]=0;//起点和终点相同，路程为0
         else
            maps[i][j]=INT_MAX;//一开始没有路，则全部是无穷大
        
        }
    int n,m;//假设有n条路,m个城市
    cin>>n;
    int a,b,c;
    for(int i=1;i<=n;i++)
    {cin>>a>>b>>c;
     maps[a][b]=c;
     maps[b][a]=c;//假设是双向路
     
        
    }
    for(int i=1;i<=m;i++)//枚举用来松弛的点
        for(int j=1;j<=m;j++)
            for(int k=1;k<=m;k++)
            {
                
                if(maps[j][k]<maps[j][i]+maps[i][k]);//通过该点松弛后距离变小了
                maps[j][k]=maps[j][i]+maps[i][k];
                
            
            }
                
    
    
    cout<<maps[][]<<endl;//求得任意2点间的最短路
}

时间复杂度（o（m^3））
可以说对于百分之90的题 这个算法都是过不了的

---

2.Dijkstra算法
这个算法还是比较常用的，一定要掌握

*核心思想：
通过“边”来松弛源点顶点到其余个顶点的路程

*具体步骤：

假设s是起点

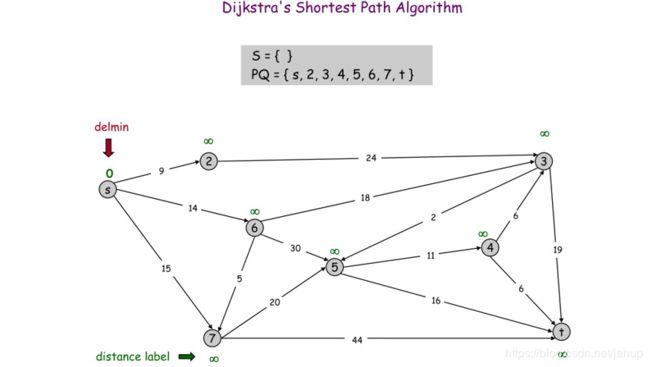
寻找s集合到PQ集合最短的边

到2点的距离是最短的

接下来到6的距离是最短的

然后是7号点



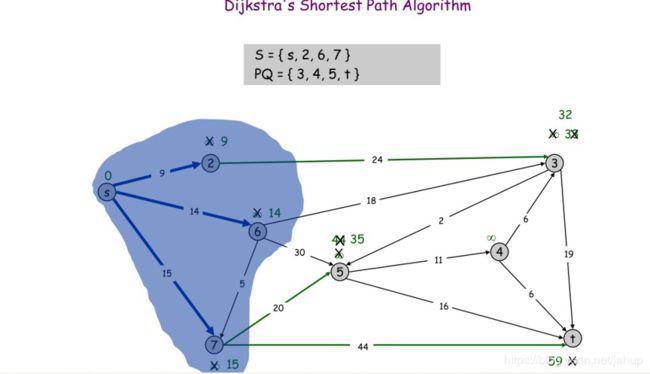
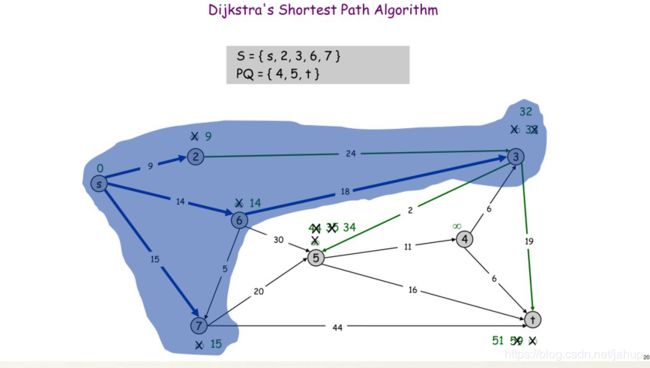
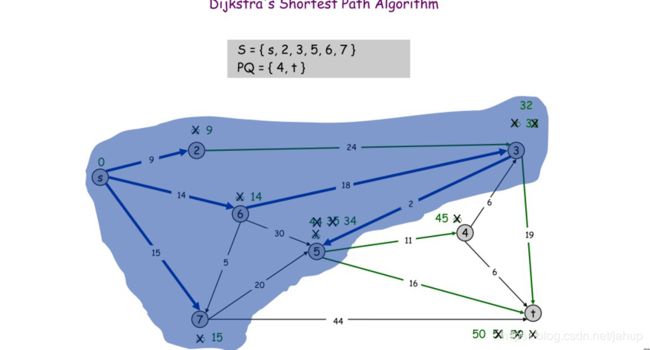
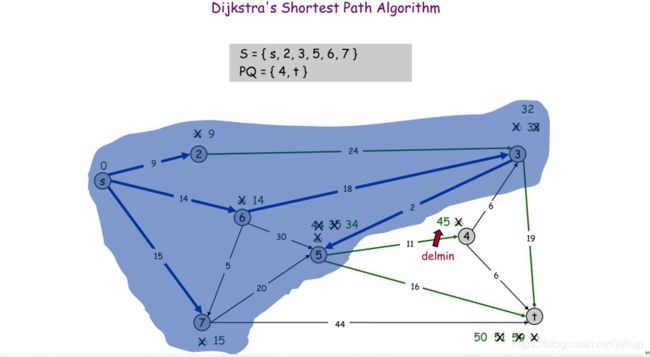
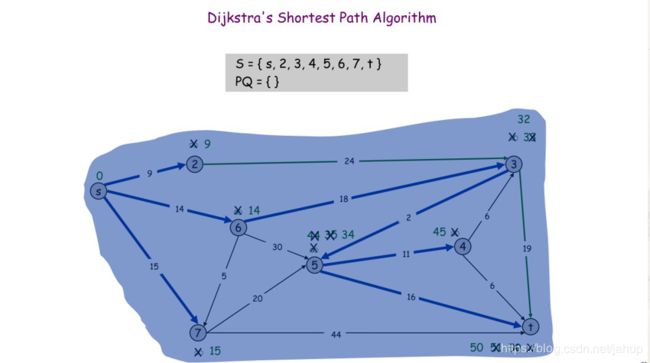
（图片是学长那偷的）

这样s点到所有点的最短路就找出来了，我们来看看代码怎么写；（记住核心思想：通过“边”来松弛源点顶点到其余个顶点的路程）

#include
#include
#include
#include
#define inf 0x3f3f3f
const int maxn=1005;
using namespace std;

typedef pair<int,int> P; //前面放到 dis[i],后面放i 

struct node{
	int v,w;
}E;
vector<node> edge[maxn];
int dis[maxn];

int main(){
	int n,m;
	int u;
	while(scanf("%d%d",&n,&m),n){
		//初始化
		for(int i=1;i<=n;i++){
			dis[i]=inf;
		} 
		//存图 
		for(int i=1;i<=m;i++){
			scanf("%d%d%d",&u,&E.v,&E.w);
			edge[u].push_back(E);
		}
		
		priority_queue <P,vector<P>,greater<P> > que;
		while(!que.empty()) que.pop();
		dis[1]=0;
		que.push(P(dis[1],1));
		while(!que.empty()){
			P now=que.top(); que.pop();
			
			int nowu=now.second;
			for(int i=0;i<edge[nowu].size();i++){
				E=edge[nowu][i]; 
				if(dis[E.v]>dis[nowu]+E.w){
					dis[E.v]=dis[nowu]+E.w;
					que.push(P(dis[E.v],E.v));
				}
			}
		}
		for(int i=1;i<=n;i++)
	    	printf("%d ",dis[i]);
	    printf("\n");
	}
	return 0;
} 

/*
6 9
1 2 1
1 3 12
2 3 9
2 4 3
3 5 5
4 3 4
4 5 13
4 6 15
5 6 4
*/

我这里写的是优先队列优化的版本时间复杂度为O（(m+n)logn），但这个算法存在一定的弊端，它无法解决带有负权边的问题，为什么了，假设有一个回路，权值之和为负数，那么我们反复走这个回路，花费可以趋近负无穷

---

3.Bellman-Ford（解决负权边单源最短路）（边是带方向的）

核心思路：
对所有的边进行n-1次松弛操作。Bellmam-Ford第k轮松弛操作其实是源点“最多经过k条边”到达其余各个顶点的最短路径。所以虽最多进行n-1次松弛操作。

基本步骤：
n-1次松弛中，反复遍历所有的边，来缩短起点到其他点的距离




优化：
在实际操作中，通常在未达到n-1轮松弛前就已经计算出了最短路，我们可以用check标记一下dis数组在某轮操作中是否发生了变化，如果没有变化，便跳出循环即可。

#include
#include 
#include
#define inf 0x3f3f3f
const int maxn=1005;
using namespace std;

int dis[maxn];
int u[maxn],v[maxn],w[maxn];

int main(){
	int n,m,check;
	while(scanf("%d%d",&n,&m),n,m){
		//存图 
		for(int i=1;i<=m;i++)
			scanf("%d%d%d",&u[i],&v[i],&w[i]);
		
		//初始化dis数组
		for(int i=1;i<=n;i++)
		   dis[i]=inf;
		dis[1]=0;
		
		//进行n-1轮松弛 
		for(int k=1;k<=n-1;k++){
			check=0;
			//遍历每一条边
			for(int i=1;i<=m;i++){
				if(dis[v[i]]>dis[u[i]]+w[i]){
					dis[v[i]]=dis[u[i]]+w[i];
					check=1;				
				}
			}                 
			if(check==0) break;
		}
		
		for(int i=1;i<=n;i++)
		    printf("%d ",dis[i]); 
		printf("\n");
		
		/*
		//判断是否有负权回路 
		int flag=0;
		for(int i=1;i<=m;i++)
		    if(dis[v[i]]>dis[u[i]]+w[i]) flag=1;
		if(flag==0) printf("no\n");
		else printf("yes\n");
		*/
	}
	return 0;
}
/*
5 5
2 3 2
1 2 -3
1 5 5
4 5 2
3 4 3
*/

（再次感谢学长学姐们的图）