相机标定原理
1 相机标定的目的
- 建立相机成像的几何模型
得到物体从三维世界映射到相机成像平面的变换矩阵,这一过程最关键的部分就是要得到相机的内参和外参。 - 校正透镜畸变
由于透镜的制造工艺(球面透镜),会使成像产生多种形式的畸变,通过标定计算畸变系数来校正各种像差
2 相机标定原理
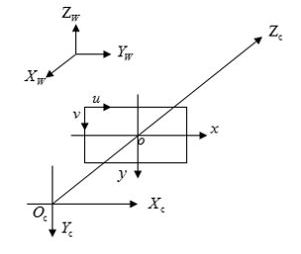
上面提到,相机标定的目的之一是为了建立物体从三维世界到成像平面上各坐标点的对应关系,所以首先我们需要定义这样几个坐标系来为整个过程做好铺垫:
- 世界坐标系(world coordinate system)
用户定义的三维世界的坐标系,为了描述目标物在真实世界里的位置而被引入,坐标 (xw, yw, zw),单位为m。 - 相机坐标系(camera coordinate system)
在相机上建立的坐标系,为了从相机的角度描述物体位置而定义,作为沟通世界坐标系和图像/像素坐标系的中间一环,坐标 (xc, yc, zc),单位为m。 - 图像坐标系(image coordinate system)
也有看到称作“像平面坐标系”的,为了描述成像过程中物体从相机坐标系到图像坐标系的投影透射关系而引入,方便进一步得到像素坐标系下的坐标,坐标 (x,y),单位为m。 - 像素坐标系(pixel coordinate system)
为了描述物体成像后的像点在数字图像上的坐标而引入,是我们真正从相机内读取到的信息所在的坐标系,坐标 (u,v),单位为pixels(像素数目)。
.
其中,构建世界坐标系只是为了更好的描述相机的位置在哪里,在双目视觉中一般将世界坐标系原点定在左相机或者右相机或者二者X轴方向的中点。
相机坐标系的Z轴与光轴重合,且垂直于图像坐标系平面并通过其原点,相机坐标系与图像坐标系原点之间的距离为焦距f(这里运用针孔成像模型,假设像平面与焦平面重合,见2.2中的针孔模型)。
像素坐标系平面u-v和图像坐标系平面x-y重合,但像素坐标系原点位于图中左上角。
2.1 世界坐标系到相机坐标系
刚体从世界坐标系转换到相机坐标系的过程,可以通过旋转和平移来得到,其变换矩阵由一个旋转矩阵R和平移向量T组合而成,变换关系如下:
.
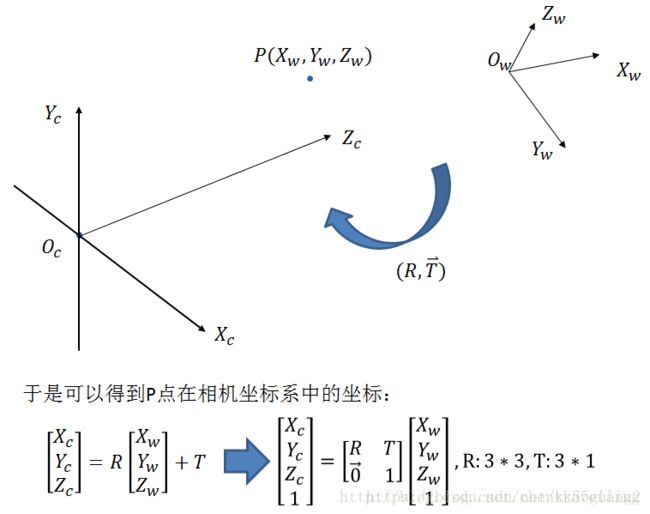
其中R有3个参数(推导见附录),T有3个参数,变换矩阵

即为外参矩阵,共6个参数。
2.2相机坐标系到图像坐标系
从相机坐标系到图像坐标系,属于透视投影关系,从3D转换到2D。也就是把三维物体成像到二维成像面的过程,一般用简化的成像模型——小孔成像模型,这种情况下图像一定会落在焦平面上。(实际光学系统中是透镜成像,一般物体的像都不会落在焦平面,成像模型比较复杂,介绍见附录)
.

为了方便观察,将像点和物点放到同一侧进行考虑,得到物点和像点的变换关系如下:
.
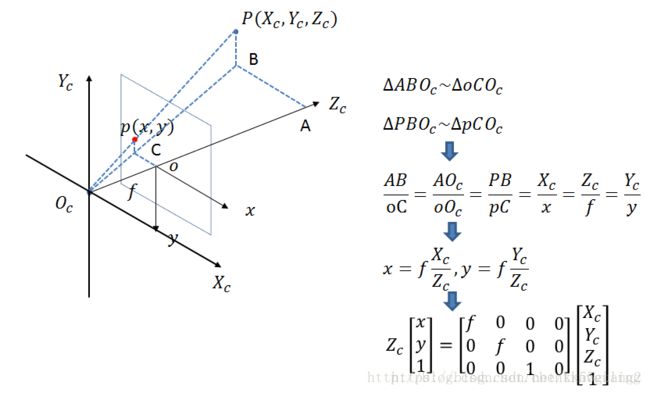
此时投影点p的单位还是mm,并不是pixel,需要进一步转换到像素坐标系。
2.3 相机中的畸变
由于实际相机模型与理想针孔模型之间的差异,图像会产生畸变,主要有径向畸变和切向畸变。
对于畸变的校正,这里仅对opencv中的畸变校正模型进行简要的叙述。
径向畸变的校正,用k1,k2,k3三个参数,(x, y)是未经纠正的点的坐标,(x_corrected, y_corrected)是校正径向畸变之后的图像坐标, r = x 2 + y 2 r = \sqrt {{x^2} + {y^2}} r=x2+y2.
x c o r r e c t e d = x ( 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 ) y c o r r e c t e d = y ( 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 ) \begin{array}{l} {x_{corrected}} = x(1 + {k_1}{r^2} + {k_2}{r^4} + {k_3}{r^6})\\ {y_{corrected}} = y(1 + {k_1}{r^2} + {k_2}{r^4} + {k_3}{r^6}) \end{array} xcorrected=x(1+k1r2+k2r4+k3r6)ycorrected=y(1+k1r2+k2r4+k3r6)
切向畸变的校正用p1,p2两个参数,其他变量的定义如径向畸变中.
x c o r r e c t e d = x + 2 p 1 x y + p 2 ( r 2 + 2 x 2 ) y c o r r e c t e d = y + p 1 ( r 2 + 2 y 2 ) + 2 p 2 x y \begin{array}{l} {x_{corrected}} = x + 2{p_1}xy + {p_2}({r^2} + 2{x^2})\\ {y_{corrected}} = y + {p_1}({r^2} + 2{y^2}) + 2{p_2}xy \end{array} xcorrected=x+2p1xy+p2(r2+2x2)ycorrected=y+p1(r2+2y2)+2p2xy
2.4 图像坐标系到像素坐标系
由于定义的像素坐标系原点与图像坐标系原点不重合,假设图像坐标系原点o在像素坐标系Ouv下的坐标为(u0,v0),每个像素点在图像坐标系x轴、y轴方向的尺寸为:dx、dy(这部分在实际硬件中为成像元件CCD或者CMOS中成像单元的中心间距,由成像单元的大小和间距决定),且像点p在实际图像坐标系下的坐标为(x,y),于是可得到像点p在像素坐标系Ouv下的坐标(u, v)为:
.

若不考虑畸变,将2.2中变换矩阵与本节变换矩阵相乘得内参矩阵为:
.
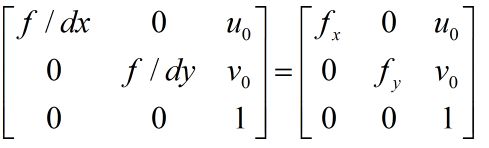
2.5 总结
综上所述,可以得到从世界坐标系的物点坐标转化到像素坐标系下的像点左边的关系式(不考虑畸变)如下:

其中相机的内参(4个)和外参(6个) 可以通过张正友标定获取。通过最终的转换关系来看,一个三维中的坐标点,的确可以在图像中找到一个对应的像素点,但是反过来,通过图像中的一个点找到它在三维中对应的点就很成了一个问题,因为我们并不知道等式左边的Zc的值。
对于相机标定的参数更详细的描述也可以参见文章:相机标定参数的描述
附录
实际成像模型简介
实际成像模型十分复杂,这里仅介绍薄透镜的简化模型,如图所示,AB为物体,A1B1为像,F为焦点,f为焦距,p和p’分别为物距和像距
.
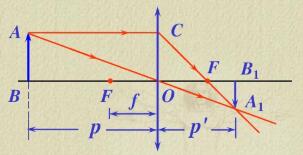
通过公式推导可得物距和像距的关系式为 1 f = 1 p + 1 p ′ \frac{1}{f} = \frac{1}{p} + \frac{1}{{p'}} f1=p1+p′1,从式中可以看到,只有当物距无穷大时,物体才会落到焦平面。顺便提一下,实际成像时,一般成像面是不会变的,为了对不同物距的物体成像,可以通过移动透镜组中某些透镜的位置可以达到变焦的效果。
三维坐标系下的旋转矩阵
三维坐标系下的任意角旋转可以看成三个步骤组成,绕x轴旋转,y轴旋转,z轴旋转。最常用的约定,即所谓“roll-pitch-yaw”系统。偏航角——Yaw,俯仰角——Pitch,翻滚角——Rool。

得最终的旋转矩阵 R = R x ( θ x ) R y ( θ y ) R z ( θ z ) R = {R_x}({\theta _x}){R_y}({\theta _y}){R_z}({\theta _z}) R=Rx(θx)Ry(θy)Rz(θz),可以看到虽然R为3*3矩阵,但是只有3个参数。
本文参考资料
- 计算机视觉:相机成像原理:世界坐标系、相机坐标系、图像坐标系、像素坐标系之间的转换
- 【机器视觉】张氏法相机标定
- 三维坐标下的旋转
说明:本文仅为部分原创,对读过的比较好的博客进行了整理和归纳,有很大一部分引用自上面资料,向资料的博主们表示感谢。