CS224n 2019 Winter 笔记（二）：神经网络（矩阵求导、反向传播推导）

笔记只记个人学习重点和难点，不追求全面，只做读书过程中的疑惑解释，既做个人心得记录，也供读者参考
如有错误，烦请留言指点，谢过！
如有错误，烦请留言指点，谢过！
如有错误，烦请留言指点，谢过！

一、交叉熵损失函数（Cross Entropy Loss Function）

上图表示某训练集${\left\{{\mathbf{x}}_i,y_i\right\}}_{i=1}^N$，${\mathbf{x}}_i$ 是 $d$ 维的输入，$y_i$ 是标签。

传统机器学习中的线性分类器，目的就是训练出一个能够较好将样本分类的直线（或是超平面），我们令其表达式的权重表示为$\mathbf{W}\in {\mathbb{R}}^{C\times d}$

在上一次课中提到，为了衡量样本 $x_i$ 属于 $y_i$ 类的概率，而用softmax函数来模拟其概率：$$p(y|x)=\frac{\exp x}{{\sum }_{i=1}^C\exp x_i}$$

在线性分类器中，目标函数的优化就是为了让预测的分类 $y\prime$ 能够以1的概率接近标签值 $y$：$$p(y|y\prime )=\frac{\exp y\prime }{{\sum }_{i=1}^C\exp y_i^{\prime }}\to 1y\prime ={\mathbf{W}}_{y\cdot }\mathbf{x}$$${\mathbf{W}}_{y\cdot }$表示矩阵的行向量

所以，在这里softmax变为：$$p\left(\mathbf{y}|\mathbf{x}\right)=\frac{\exp ({\mathbf{W}}_{y\cdot }\mathbf{x})}{{\sum }_{c=1}^C\exp ({\mathbf{W}}_{c\cdot }\mathbf{x})}=softmax(f_y)$$其中，${\mathbf{W}}_{y\cdot }\mathbf{x}={\sum }_{i=1}^d{\mathbf{W}}_{yi}{x}_i=f_y$，这个式子也可以写成向量 $\boldsymbol{x} $ 与权重矩阵 $\mathbf{W}$ 相乘的形式：$f=\mathbf{W}\mathbf{x}$

此外，对于每一个训练样本$({\mathbf{x}}_i,y_i)$来说，训练的最终目的是为了最大化上述概率，等价于最小化该概率的负对数形式：$$\underset{({\mathbf{x}}_i,y_i)}{\max }\left\{p\left(\mathbf{y}|\mathbf{x}\right)\right\}\iff \underset{({\mathbf{x}}_i,y_i)}{\min }\left\{-\log p\left(\mathbf{y}|\mathbf{x}\right)\right\}=\underset{({\mathbf{x}}_i,y_i)}{\min }-\log \left(\frac{\exp (f_y)}{{\sum }_{c=1}^C\exp (f_c)}\right)$$

如果令真实的概率分布为$p$，预测的概率分布为$q$，则交叉熵定义如下：$$H(p,q)=-\sum _{c=1}^{C}p(c)\log q(c)$$

考虑上述softmax模拟的概率，在具体的操作中，我们一般把多分类的类别概率使用独热（one-hot）编码表示，这也是我们预测的概率要逼近的真实概率。以三分类为例（如下表），类别标签中只有1个类别为1，其余为零，分别表示该类型的概率。而在预测的时候，则会有一个较大的类别趋近于1，其他的都是趋近于0的。真实值的类别为2。
参考博客：[1]2019斯坦福CS224n深度学习自然语言处理笔记（3）——分类模型与神经网络）

类型名	类别1	类别2	类别3
真实值 $p(c)$	0	1	0
预测值 $q(c)$	0.05	0.9	0.05

也就是说，对于真实值 $p(c)$ 来说，只有“类别2”才起作用，因为其余均为0。因此，平均交叉加粗样式熵损失函数可以表示为：$$J(\theta )=\frac{1}{N}\sum _{i=1}^N-\log \left(\frac{e^{f_{yi}}}{{\sum }_{c=1}^C{e}^{f_c}}\right)$$

二、Derivative of Matrix

符号约定：

• 标量由小写字母表示，如 $x$
• 向量由粗体小写字母表示，如 $\mathbf{a}$
• 矩阵由大写加粗字母表示，如 $\mathbf{A}$
• 如无特殊说明，向量均表示列向量（行向量通过列向量转置来表示，如 ${\mathbf{a}}^T$）
• 如无特殊说明，向量的元素表示均为行向量表示，如$\{x_1,\cdots ,x_n\}$表示多个标量按水平方向排列，即行向量，相应的$\{x_1,\cdots ,x_n{\}}^T$则表示列向量

（一）矩阵的几种乘积

（1）点积（内积）

• 向量点积，也称为内积：$$\mathbf{a}\cdot \mathbf{b}=\sum _{i=1}^n{a}_i{b}_i$$
• 矩阵内积（两个矩阵对应元素乘积，并求和）：$$\mathbf{A}\cdot \mathbf{B}=\sum _{i=1}^m\sum _{j=1}^n{a}_{ij}{b}_{ij}=tr({\mathbf{A}}^T\mathbf{B})$$

（2）点乘（hadamard product,哈达码积）

矩阵点乘，也称元素积(element-wise product, point-wise product)，表示两个矩阵对应元素相乘，要求两个矩阵大小完全一致。若${\mathbf{A}}_{m\times n},{\mathbf{B}}_{m\times n}$，则有：$$\mathbf{A}\ast \mathbf{B}={\left[a_{ij}{b}_{ij}\right]}_{m\times n}$$

（3）克罗内克积（kronecker product）

也称直积、张量积。若${\mathbf{A}}_{m\times n},{\mathbf{B}}_{p\times q}$，则有：$$\mathbf{A}\otimes \mathbf{B}={\left[\begin{array}{ccc}{a}_{11}\mathbf{B}& \cdots & a_{1n}\mathbf{B}\\ ⋮& & ⋮\\ a_{m1}\mathbf{B}& \cdots & a_{mn}\mathbf{B}\end{array}\right]}_{mp\times nq}$$

（二）矩阵的运算

来源博客：矩阵求导术、矩阵微积分（一）

关于矩阵的函数：$$\mathrm{d}f=\frac{\partial f}{\partial X}\cdot \mathrm{d}X\text{\hspace{1em}(1)}$$

（1）微分运算

1. 加（减）法 $$\mathrm{d}(\mathbf{A}\pm \mathbf{B})=\mathrm{d}\mathbf{A}\pm \mathrm{d}\mathbf{B}$$
2. 乘法$$\mathrm{d}(\mathbf{A}\mathbf{B})=(\mathrm{d}\mathbf{A})\mathbf{B}+\mathbf{A}\mathrm{d}\mathbf{B}$$
3. 转置$$\mathrm{d}{\mathbf{A}}^T=(\mathrm{d}\mathbf{A}{)}^T$$
4. 迹（trace）$$\mathrm{d}\left(tr(\mathbf{A})\right)=tr(\mathrm{d}\mathbf{A})$$
5. $$\mathrm{d}\mathbf{A}=0$$$\mathbf{A}$是常量矩阵， $0$是零矩阵
6. 推论： 若$\mathbf{A},\mathbf{B}$是常量矩阵，则：$$\mathrm{d}(\mathbf{A}\mathbf{X}\mathbf{B})=\mathbf{A}(\mathrm{d}\mathbf{X})\mathbf{B}$$
7. 行列式$$\mathrm{d}|\mathbf{A}|=tr(A^{\ast }\mathrm{d}\mathbf{A})$$其中 ${\mathbf{A}}^{\ast }$ 表示 $\mathbf{A}$ 的伴随矩阵。如果 $\mathbf{A}$ 可逆，则又有：$$\mathrm{d}|\mathbf{A}|=|\mathbf{A}|tr({\mathbf{A}}^{-1}\mathrm{d}\mathbf{A})$$
8. Hadamard 积：逐元素乘法
   定义矩阵$\mathbf{A}$与$\mathbf{B}$的Hadamard积为${\left[A_{ij}{B}_{ij}\right]}_{n\times m}$，记作$\mathbf{A}\odot \mathbf{B}$，有结论：$$\mathrm{d}(\mathbf{A}\odot \mathbf{B})=\mathrm{d}\mathbf{A}\odot \mathbf{B}+\mathbf{A}\odot \mathrm{d}\mathbf{B}$$
9. 逐元素标量函数$$\mathrm{d}h(\mathbf{A})=h^{\prime }(\mathbf{A})\odot \mathrm{d}\mathbf{A}$$其中，$h(\mathbf{X})$ 为对矩阵 $\mathbf{X}$ 进行逐元素运算的标量函数
10. 逆 $$\mathrm{d}{\mathbf{X}}^{-1}=-{\mathbf{X}}^{-1}(\mathrm{d}\mathbf{X}){\mathbf{X}}^{-1}$$

（2）点乘运算

注意：点乘是矩阵对应元素相乘，要求参加运算的两个矩阵形状相同

1. 定义式$$\mathbf{A}\cdot \mathbf{B}=tr({\mathbf{A}}^T\mathbf{B})$$对于向量来说，该式可以进一步简化：$\mathbf{a}\cdot \mathbf{b}={\mathbf{a}}^T\mathbf{b}$
2. 交换律$$\mathbf{A}\cdot \mathbf{B}=\mathbf{B}\cdot \mathbf{A}$$
3. 加法分配律$$\mathbf{A}\cdot (\mathbf{B}+\mathbf{C})=\mathbf{A}\cdot \mathbf{B}+\mathbf{A}\cdot \mathbf{C}$$
4. 与逐元素乘法的结合律$$\mathbf{A}\cdot (\mathbf{B}\odot \mathbf{C})=(\mathbf{A}\odot \mathbf{B})\cdot \mathbf{C}$$
5. 转置的交换$${\mathbf{A}}^T\cdot \mathbf{B}=\mathbf{A}\cdot {\mathbf{B}}^T$$

（3）迹运算

注意：迹运算的对象必须为方阵

1. 标量的迹等于其自身$$tr(x)=x$$
2. 线性$$tr(\mathbf{A}\pm \mathbf{B})=tr(\mathbf{A})\pm tr(\mathbf{B})$$
3. 乘法可交换性$$tr(\mathbf{A}\mathbf{B})=tr(\mathbf{B}\mathbf{A})$$要求 $\mathbf{A}$ 和 ${\mathbf{B}}^T$ 的形状相同，这样才能保证 $\mathbf{A}\mathbf{B}$ 为方阵
4. 转置迹不变$$tr({\mathbf{A}}^T)=tr(\mathbf{A})$$
5. 迹与点乘的转换$$tr(A\mathbf{B})={\mathbf{A}}^T\cdot \mathbf{B}$$

（4）其他运算

$$\begin{array}{rl}& ({\mathbf{A}}^T{)}^T=\mathbf{A}\\ & (\mathbf{A}\mathbf{B}{)}^T={\mathbf{B}}^T{\mathbf{A}}^T\\ & ({\mathbf{A}}^{-1}{)}^{-1}=\mathbf{A}\\ & \mathbf{A}{\mathbf{A}}^{-1}={\mathbf{A}}^{-1}\mathbf{A}=I\\ & (\mathbf{A}\mathbf{B}{)}^{-1}={\mathbf{B}}^{-1}{\mathbf{A}}^{-1}\\ & ({\mathbf{A}}^T{)}^{-1}=({\mathbf{A}}^{-1}{)}^T\\ & |{\mathbf{A}}^{-1}|=|\mathbf{A}{|}^{-1}\\ & (k\mathbf{A}{)}^{-1}=k^{-1}{\mathbf{A}}^{-1}\end{array}$$

（三）标量对矩阵求导

参考博客：矩阵求导术

原则：标量 $f$对矩阵 $\mathbf{X}$ 求导，遵循一个原则，即 $f$对矩阵 $\mathbf{X}$ 的导数 $\frac{\mathrm{d}f}{\mathrm{d}\mathbf{X}}$形状与矩阵 $\mathbf{X}$ 的形状一致。

例：设 $y={\mathbf{a}}^T\mathbf{X}\mathbf{b}$，求 $\frac{\partial y}{\partial \mathbf{X}}$。其中 $\mathbf{a}$ 为 $m\times 1$ 向量，$\mathbf{X}$ 为 $m\times n$ 矩阵，$\mathbf{b}$ 为 $n\times 1$ 向量，$y$ 为标量。

解： $$\begin{array}{rl}\mathrm{d}y& ={\mathbf{a}}^T\mathrm{d}\mathbf{X}\mathbf{b}\\ & =tr({\mathbf{a}}^T\mathrm{d}\mathbf{X}\mathbf{b})\\ & =tr(\mathbf{b}{\mathbf{a}}^T\mathrm{d}\mathbf{X})\\ & =tr((\mathbf{a}{\mathbf{b}}^T{)}^T\mathrm{d}\mathbf{X})\\ & =\mathbf{a}{\mathbf{b}}^T\cdot \mathrm{d}\mathbf{X}\end{array}$$根据公式 $(1)$ 得到： $$\frac{\partial y}{\partial \mathbf{X}}=\mathbf{a}{\mathbf{b}}^T\in {\mathbb{R}}^{m\times n}$$与矩阵 $\mathbf{X}$ 的形状一致。

例：线性回归的损失函数定义为 $l=||\mathbf{X}\mathbf{w}-\mathbf{y}|{|}_2^2$，求 $\mathbf{w}$ 的最小二乘估计，即 $\mathbf{w}$ 为何值时 $l$ 可取得最小值。其中 $\mathbf{y}$ 为 $m\times 1$ 列向量，$\mathbf{X}$ 为 $m\times n$ 矩阵，$\mathbf{w}$ 为 $n\times 1$ 向量，$l$ 为标量
解：要求极小值，只需找到 $\frac{\partial l}{\partial \mathbf{w}}$ 的零点。
我们的运算规则中并未定义二阶范数的微分，但根据向量范数的定义，我们可以将它表示成内积的形式：$$l=(\mathbf{X}\mathbf{w}-\mathbf{y})\cdot (\mathbf{X}\mathbf{w}-\mathbf{y})=(\mathbf{X}\mathbf{w}-\mathbf{y}{)}^T(\mathbf{X}\mathbf{w}-\mathbf{y})$$
接下来，求 $l$ 对 $\mathbf{w}$ 的微分：
$$\begin{array}{rl}\mathrm{d}l& =\mathrm{d}(\mathbf{X}\mathbf{w}-\mathbf{y}{)}^T(\mathbf{X}\mathbf{w}-\mathbf{y})+(\mathbf{X}\mathbf{w}-\mathbf{y}{)}^T\mathrm{d}(\mathbf{X}\mathbf{w}-\mathbf{y})\\ & =(\mathbf{X}\mathrm{d}\mathbf{w}{)}^T(\mathbf{X}\mathbf{w}-\mathbf{y})+(\mathbf{X}\mathbf{w}-\mathbf{y}{)}^T(\mathbf{X}\mathrm{d}\mathbf{w})\\ & =2(\mathbf{X}\mathbf{w}-\mathbf{y}{)}^T\mathbf{X}\mathrm{d}\mathbf{w}\\ & =2{\mathbf{X}}^T(\mathbf{X}\mathbf{w}-\mathbf{y})\cdot \mathrm{d}\mathbf{w}\end{array}$$根据公式 $(1)$ 可得：$$\frac{\partial l}{\partial \mathbf{w}}=2X^T(\mathbf{X}\mathbf{w}-\mathbf{y})$$
令 $\frac{\partial l}{\partial \mathbf{w}}=0$ 得（加粗的 $0$ 代表零向量，其形状与 $\mathbf{w}$ 相同）：
$$\mathbf{w}=(X^{T}X{)}^{-1}{X}^T\mathbf{y}$$

（四）矩阵对矩阵求导

这部分内容主要以cs224n官方给的矩阵求导的pdf为主，下载请戳这里

（1）Jacobian Matrix

假设函数 $\mathbf{f}:{\mathbb{R}}^n\to {\mathbb{R}}^m$ 能将 $n$ 维向量映射为 $m$ 维：$$\mathbf{f}(\mathbf{x})=\left[f_1(x_1,\cdots ,x_n),f_2(x_1,\cdots ,x_n),\cdots ,f_m(x_1,\cdots ,x_n)\right]$$则对应的Jacobian Matrix为：$$\frac{\partial \mathbf{f}}{\partial \mathbf{x}}={\left[\begin{array}{ccc}\frac{\partial f_1}{x_1}& \cdots & \frac{\partial f_1}{x_n}\\ ⋮& \ddots & ⋮\\ \frac{\partial f_m}{x_1}& \cdots & \frac{\partial f_m}{x_n}\end{array}\right]}_{m\times n}$$

利用Jacobian 矩阵和链式法则，即可计算矩阵的导数，下面列举一些结论，方便以后手动计算。

（2）结论

1.矩阵乘以列向量，对列向量求导

若$\mathbf{W}\in {\mathbb{R}}^{n\times m},\mathbf{x}\in {\mathbb{R}}^{m\times 1}$且$\mathbf{z}=\mathbf{W}\mathbf{x}$，则$$\frac{\partial \mathbf{z}}{\partial \mathbf{x}}=\mathbf{W}$$

证明：将$\mathbf{z}$看作一个映射函数：${\mathbb{R}}^m\to {\mathbb{R}}^n$ （因为$\mathbf{x}$由$m$维变为$n$维），其中${\mathbf{z}}_i={\sum }_{k=1}^m{W}_{ik}{x}_k$，则对应的Jacobian矩阵是 $n\times m$ 维的：
$$\begin{array}{rl}\frac{\partial \mathbf{z}}{\partial \mathbf{x}}& ={\left[\begin{array}{ccc}\frac{z_1}{x_1}& \cdots & \frac{z_1}{x_m}\\ ⋮& \ddots & ⋮\\ \frac{z_n}{x_1}& \cdots & \frac{z_n}{x_m}\end{array}\right]}_{n\times m}\\ & ={\left[\begin{array}{ccc}{w}_{11}& \cdots & w_{1m}\\ ⋮& \ddots & ⋮\\ w_{n1}& \cdots & w_{nm}\end{array}\right]}_{n\times m}\\ & =\mathbf{W}\end{array}$$

2.行向量乘以矩阵，对行向量求导

若${\mathbf{x}}^T\in {\mathbb{R}}^{1\times m},\mathbf{W}\in {\mathbb{R}}^{m\times n}$且$\mathbf{z}=\mathbf{x}\mathbf{W}$，则$$\frac{\partial \mathbf{z}}{\partial {\mathbf{x}}^T}={\mathbf{W}}^T$$（证明同上，略）

3.向量对自身求导

若列向量$\mathbf{z}=\mathbf{x}$，则$$\frac{\partial \mathbf{z}}{\partial \mathbf{x}}=\mathbf{I}$$

4.向量的逐元素函数求导

若$\mathbf{x}\in {\mathbb{R}}^{m\times 1},\mathbf{z}\in {\mathbb{R}}^{m\times 1}$且$\mathbf{z}=f(\mathbf{x})$，其中 $f$ 是对向量进行逐元素操作的函数，即 $z_i=f(x_i)$，则$$formula$$
证明：将$\mathbf{f}$看作一个映射函数：${\mathbb{R}}^m\to {\mathbb{R}}^m$ ，则对应的Jacobian矩阵是 $m\times m$ 维的：
$$\begin{array}{rl}\frac{\partial \mathbf{z}}{\partial \mathbf{x}}& ={\left[\begin{array}{ccc}\frac{\partial z_1}{\partial x_1}& \cdots & \frac{\partial z_1}{\partial x_m}\\ ⋮& \ddots & ⋮\\ \frac{\partial z_m}{\partial x_1}& \cdots & \frac{\partial z_m}{\partial x_m}\end{array}\right]}_{m\times m}\\ & ={\left[\begin{array}{cccc}{f}^{\prime }(x_1)& 0& \cdots & 0\\ 0& f^{\prime }(x_2)& \ddots & ⋮\\ ⋮& ⋮& \ddots & 0\\ 0& 0& \cdots & f^{\prime }(x_m)\end{array}\right]}_{m\times m}\\ & =diag\left(f^{\prime }(x_1),f^{\prime }(x_1),\cdots ,f^{\prime }(x_m)\right)\end{array}$$
也可写成$$\frac{\partial \mathbf{z}}{\partial \mathbf{x}}=diag(f^{\prime }(\mathbf{x}))$$

Since multiplication by a diagonal matrix is the same as doing elementwise multiplication by the diagonal, we could also write $\circ f^{\prime }(\mathbf{x})$ when applying the chain rule
由于乘以一个对角阵，等同于按element-wise乘以一个对角阵，所以当应用链式法则时也写作$\circ f^{\prime }(\mathbf{x})$

三、人工神经元（Artificial Neurals）

神经元是一个通用的计算单元，具有 $n$ 个输入和 1 个输出，如图所示。$f$ 是非线性激活函数，$x_i,w_i$是输入和权重，$b$ 是偏置。输入经加权求和偏置后，通过激活函数 $f$ 的作用输出，即为神经元的输出。公式如下：$$\begin{gathered} h_{\mathbf{w},\mathbf{b}}(x_i)=f(w_i{x}_i+b_i) \\ f(z_i)=\frac{1}{1+e^{-z_i}} \\ \mathbf{x}=\left[x_1,\cdots ,x_n\right]\mathbf{w}=\left[w_1,\cdots ,w_n\right]\mathbf{b}=\left[b_1,\cdots ,b_n\right]\mathbf{z}=\left[z_1,\cdots ,z_n\right] \end{gathered}$$也可以表示向量形式：$$h=f\left({\mathbf{w}}^T\mathbf{x}+\mathbf{b}\right)=\frac{1}{1+\exp \left(-\left({\mathbf{w}}^T\mathbf{x}+\mathbf{b}\right)\right)}$$

单层的神经网络

参考博客：神经网络浅讲：从神经元到深度学习

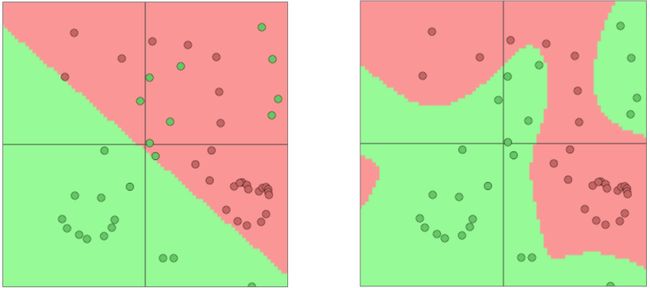
一个神经元就可以看成是一个单层的神经网络。从形式上来看，它与感知机（感知机是基础的线性二分类模型）非常像。但由于感知机通常采用阶跃激活函数，即$$f(x)=\{\begin{array}{l}n/2,\text{if }w\cdot x+b>0\\ 3n+1,\text{otherwise}\end{array}$$缺乏非线性的激活函数，故只能做线性决策，下图（左）。相对于感知机，神经元采用非线性激活函数的神经元可以拟合曲线函数，下图（右）。

多层的神经网络

Without non-linearities, deep neural networks can’t do anything more than a linear transform
译：没有非线性，深度神经网络不能比线性变换做的更多

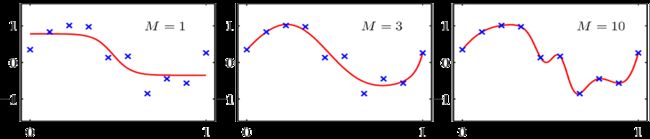
神经网络之所以能够拟合各种非线性函数，主要的功劳都归于非线性函数$f$。神经网络每深一层都可以看作是一次线性变换，layer越多就拟合更复杂的非线性函数（如下图）。

四、神经网络（Neural Networks）

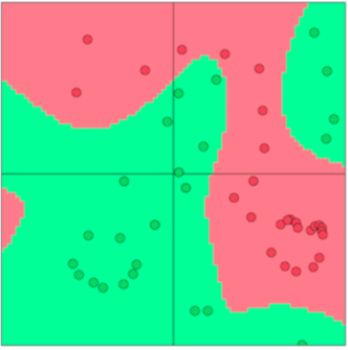
We established in our previous discussions the need for non-linear classifiers since most data are not linearly separable and thus, our classification performance on them is limited. Neural networks are
a family of classifiers with non-linear decision boundary as seen in Figure 1.
译：我们在之前的讨论中确定了非线性分类器的必要性，因为大多数数据不是线性可分的，它们的分类性能是有限的。神经网络是一类具有非线性决策边界的分类器，如图1所示。

一般来说，人们较喜欢选择“sigmoid”（也称为“二元逻辑函数”）作为神经元的激活函数。$$sigmoid(x)=\frac{1}{1+e^{-x}}$$函数图像如下：
可以看出，sigmoid函数连续光滑且严格单调，以(0,0.5)中心对称，是一个非常良好的阈值函数。此外，Sigmoid函数的导数是其本身的函数，即：$f^{\prime }(x)=f(x)\left(1-f(x)\right)$，计算非常方便，也非常节省计算时间。

因此，即可得到上述所列的神经元公式。公式如下：$$\begin{gathered} h_{\mathbf{w},\mathbf{b}}(x_i)=f(w_i{x}_i+b_i) \\ f(z_i)=\frac{1}{1+e^{-z_i}} \\ \mathbf{x}=\left[x_1,\cdots ,x_n\right]\mathbf{w}=\left[w_1,\cdots ,w_n\right]\mathbf{b}=\left[b_1,\cdots ,b_n\right]\mathbf{z}=\left[z_1,\cdots ,z_n\right] \end{gathered}$$即：$$h_{\mathbf{w},\mathbf{b}}(x_i)=\frac{1}{1+e^{-(w_i{x}_i+b_i)}}$$也可以表示向量形式：$$h=f\left({\mathbf{w}}^T\mathbf{x}+\mathbf{b}\right)=\frac{1}{1+\exp \left(-\left({\mathbf{w}}^T\mathbf{x}+\mathbf{b}\right)\right)}$$

将上述神经元的思想扩展到多个神经元，考虑多个神经元共享输入 $\mathbf{x}$ 的情况，如下图所示。

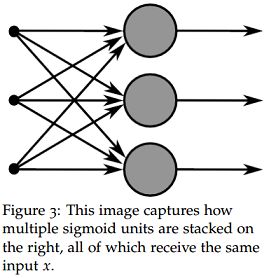
为清晰描述，下面先统一数学表示：

• $\mathbf{x}=\{x_1,\cdots ,x_n{\}}^T\in {\mathbb{R}}^{n\times 1}$为输入
• ${\mathbf{w}}^{(i)}=\{w_1,\cdots ,w_n{\}}^T\in {\mathbb{R}}^{m\times 1}$ 表示第$i$个神经元的权重向量
• $\mathbf{W}=\{{{\mathbf{w}}^{(1)}}^T,\cdots ,{{\mathbf{w}}^{(m)}}^T{\}}^T\in {\mathbb{R}}^{m\times n}$表示整个网络的权重矩阵
• $\mathbf{b}=\{b_1,\cdots ,b_m{\}}^T\in {\mathbb{R}}^{m\times 1}$ 为偏置
• $\mathbf{z}=\mathbf{W}\mathbf{x}+\mathbf{b}$
• $\sigma (\cdot )$表示激活函数
• $\mathbf{h}=\sigma (\mathbf{z})=\sigma (\mathbf{W}\mathbf{x}+\mathbf{b})=\{h_1,\cdots ,h_m{\}}^T\in {\mathbb{R}}^{m\times 1}$为神经元输出

综上即有：$$h_i=\frac{1}{1+\exp \left({{\mathbf{w}}^{(i)}}^T\mathbf{x}+{\mathbf{b}}_i\right)}$$

（一）前馈计算

从上图可以发现，图片显示的是单层多神经元的网络，它有$n$个输出。假设有这么一个命名实体识别（NER）的task，需要在下面句子中找出中心词“Pairs”是不是命名实体：

“Museums in Paris are amazing”

notes03中说到：

it is very likely that we would not just want to capture the presence of words in the window of word vectors
but some other interactions between the words in order to make the classification
译：我们很有可能不仅想要捕获单词向量窗口中的单词，还想要捕获单词之间的其他交互，以便进行分类

我们更希望捕获词之间的信息，因此以窗口内的几个词向量的combine作为输入。此外，我们不希望网络的输出有$n$个，而是类似得分的一个输出，直接得出“Pairs”是不是命名实体的结果。这时就需对上图网络进行修改，如下图：

前馈传播示意图

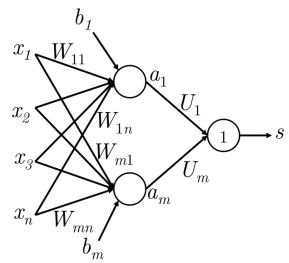
Dimensions for a single hidden layer neural network: If we represent each word using a 4-dimensional word vector and we use a 5-word window as input, then the input $\mathbf{x}\in {\mathbb{R}}^{20}$. If we use 8 sigmoid units in the hidden layer and generate 1 score output from the activations, then $\mathbf{W}\in {\mathbb{R}}^{8\times 20},\mathbf{b}\in {\mathbb{R}}^8,\mathbf{u}\in {\mathbb{R}}^{8\times 1},s\in \mathbb{R}$. The stage-wise feed-forward computation is then:$$\begin{gathered} \mathbf{z}=\mathbf{W}\mathbf{x}+\mathbf{b} \\ \mathbf{h}=\sigma (\mathbf{z}) \\ s={\mathbf{u}}^T\mathbf{h} \end{gathered}$$
译：只有一个隐含层的神经网络的维度：如果我们使用4维的词向量表示word，且滑动窗口大小为5，那么输入向量为$\mathbf{x}\in {\mathbb{R}}^{20}$。如果在隐含层中使用8个sigmoid函数，并从激活中生成一个分数输出，那么$\mathbf{W}\in {\mathbb{R}}^{8\times 20},\mathbf{b}\in {\mathbb{R}}^8,\mathbf{u}\in {\mathbb{R}}^{8\times 1},s\in \mathbb{R}$，前馈计算公式为：
$$\begin{gathered} \mathbf{z}=\mathbf{W}\mathbf{x}+\mathbf{b} \\ \mathbf{h}=\sigma (\mathbf{z}) \\ s={\mathbf{u}}^T\mathbf{h} \end{gathered}$$

如上所述，修改就是多加一层神经元，新增的权重向量为$\mathbf{u}\in {\mathbb{R}}^{m\times 1}$

（二）最大间隔目标函数（Maximum margin objection function）

在上述NER任务中，我们目标是：

ensure that the score computed for “true” labeled data points is higher than the score computed for
“false” labeled data points.
确保正确标签数据点的分数要大于错误标签数据点的分数

换句话说，就是正样本的分数要高于负样本的分数。于是，假设有两个样本，一个是正样本，一个是负样本。

• Museums in Paris are amazing（正样本）
• Not all museums in Paris（负样本）

正样本的center word是 “Paris”，是命名实体；负样本的center word是 “museums”，不是命名实体。假设正样本和负样本的分数分别为 $s,s_c$，那么训练神经网络的目标就是（具体推导详见note03）：$$\min J=\max (1+s_c-s,0)$$
其中，$s={\mathbf{u}}^T\sigma \left(\mathbf{W}\mathbf{x}+\mathbf{b}\right),s_c={\mathbf{u}}^T\sigma \left(\mathbf{W}{\mathbf{x}}_c+\mathbf{b}\right)$

（三）反向传播

训练过程就是最小化目标函数的过程，具体怎么最小化呢？用梯度下降法（或者梯度下降的变种算法）！

在神经网络的训练中，利用反向传播算法将目标函数的梯度在网络中反向传播，权重根据梯度调整值，并重复迭代。迭代的具体公式如下：$${\theta }^{(t+1)}={\theta }^{(t)}-\alpha {\nabla }_{{\theta }^{(t)}}J$$

下面，举个例子说明反向传播的工作流程。下图显示的是一个“4-2-1”的神经网络。做以下表示说明：

• $\mathbf{x}=\{x_1,\cdots ,x_4{\}}^T\in {\mathbb{R}}^{4\times 1}$为网络的输入
• $s$ 为网络的输出
• ${\mathbf{z}}_j^{(k)}$ 表示第$k$层的第$j$个神经元的输入（标量）
• ${\mathbf{z}}^{(k)}$ 表示第$k$层的输入
• ${\mathbf{h}}_j^{(k)}=\sigma ({\mathbf{z}}_j^{(k)})$ 表示第$k$层的第$j$个神经元的输出（标量）
• ${\mathbf{h}}^{(k)}=\sigma ({\mathbf{z}}^{(k)})$ 表示第$k$层的输出
• ${\delta }_j^{(k)}$ 表示来自${\mathbf{z}}_j^{(k)}$的反向传播误差
• ${\mathbf{W}}^{(k)}$表示第$k$层到第$k+1$层的权重矩阵
• ${\mathbf{W}}_{ij}^{(k)}$表示第 $k$ 层的第 $j$ 个神经元到第 $k+1$ 层的第 $i$ 个神经元的权重（是一个标量，见“前馈传播示意图”）

于是，在这个“4-2-1”的神经网络中，有下列式子成立：
$$\begin{array}{rl}s={\mathbf{h}}_1^{(3)}& ={\mathbf{W}}^{(2)}{\mathbf{h}}^{(2)}=\mathbf{U}{\mathbf{h}}^{(2)}\\ {\mathbf{h}}^{(1)}& ={\mathbf{z}}^{(1)}=\mathbf{x}\text{（第一层是输入层，不是隐藏层，无激活函数）}\\ {\mathbf{W}}^{(1)}& =\mathbf{W}\\ {\mathbf{W}}^{(2)}& =\mathbf{U}\\ {\mathbf{z}}^{(k)}& ={\mathbf{W}}^{(k-1)}{\mathbf{h}}^{(k-1)}\end{array}$$
各参数的维度为：
$$\begin{array}{rl}s{x}_i{\mathbf{z}}_i^{(k)}{\mathbf{h}}_i^{(k)}{\mathbf{W}}_{ij}^{(k)}& \in \mathbb{R}\\ \mathbf{x},{\mathbf{z}}^{(1)},{\mathbf{z}}^{(2)},{\mathbf{h}}^{(1)}& \in {\mathbb{R}}^{4\times 1}\\ {\mathbf{h}}^{(2)}& \in {\mathbb{R}}^{2\times 1}\\ {\mathbf{W}}^{(1)}& \in {\mathbb{R}}^{2\times 4}\\ {\mathbf{W}}^{(2)}=\mathbf{U}& \in {\mathbb{R}}^{1\times 2}\end{array}$$
注意一点，图中第$k$层的权重 ${\mathbf{W}}_{ij}^{(k)}$ 在第$k+1$层中只对 ${\mathbf{z}}_i^{(k+1)}$ 有贡献，从而得到 ${\mathbf{h}}_i^{(k+1)}$，这对接下来的推导很重要。

1、目标函数对权重的梯度计算

我们计算目标函数对权重 ${\mathbf{W}}_{ij}^{(1)}$ 的梯度：
$$\begin{array}{rl}\frac{\partial s}{\partial {\mathbf{W}}_{ij}^{(1)}}& =\frac{\partial {\mathbf{W}}^{(2)}{\mathbf{h}}^{(2)}}{\partial {\mathbf{W}}_{ij}^{(1)}}\leftarrow s={\mathbf{W}}^{(2)}{\mathbf{h}}^{(2)}\\ & =\frac{\partial {\mathbf{W}}_i^{(2)}{\mathbf{h}}_i^{(2)}}{\partial {\mathbf{W}}_{ij}^{(1)}}\leftarrow {\mathbf{W}}_i^{(2)},{\mathbf{h}}_i^{(2)}\text{都是向量，只有第 i 个元素起作用}\\ & ={\mathbf{W}}_i^{(2)}\cdot \frac{\partial {\mathbf{h}}_i^{(2)}}{\partial {\mathbf{W}}_{ij}^{(1)}}\\ & ={\mathbf{W}}_i^{(2)}\cdot \frac{\partial {\mathbf{h}}_i^{(2)}}{\partial {\mathbf{z}}_i^{(2)}}\cdot \frac{\partial {\mathbf{z}}_i^{(2)}}{{\mathbf{W}}_{ij}^{(1)}}\\ & ={\mathbf{W}}_i^{(2)}\cdot f^{\prime }\left({\mathbf{z}}_i^{(2)}\right)\cdot \frac{\partial {\mathbf{z}}_i^{(2)}}{{\mathbf{W}}_{ij}^{(1)}}\leftarrow {\mathbf{h}}_i^{(2)}是{\mathbf{z}}_i^{(2)}的函数\\ & ={\mathbf{W}}_i^{(2)}\cdot f^{\prime }\left({\mathbf{z}}_i^{(2)}\right)\cdot \frac{\partial }{{\mathbf{W}}_{ij}^{(1)}}\left({\mathbf{b}}_i^{(1)}+\sum _{k=1}^4{\mathbf{W}}_{ik}^{(1)}{\mathbf{h}}_k^{(1)}\right)\\ & ={\mathbf{W}}_i^{(2)}\cdot f^{\prime }\left({\mathbf{z}}_i^{(2)}\right)\cdot \frac{\partial }{{\mathbf{W}}_{ij}^{(1)}}\left(\sum _{k=1}^4{\mathbf{W}}_{ik}^{(1)}{\mathbf{h}}_k^{(1)}\right)\\ & ={\mathbf{W}}_i^{(2)}\cdot f^{\prime }\left({\mathbf{z}}_i^{(2)}\right)\cdot {\mathbf{h}}_j^{(1)}\leftarrow i=j时才有非零值\\ & ={\delta }_i^{(2)}\cdot {\mathbf{h}}_j^{(1)}\leftarrow 令{\delta }_i^{(2)}={\mathbf{W}}_i^{(2)}\cdot f^{\prime }\left({\mathbf{z}}_i^{(2)}\right)\end{array}$$
最终发现，目标函数对权重 ${\mathbf{W}}_{ij}^{(1)}$ 的梯度就是${\delta }_i^{(2)}{\mathbf{h}}_j^{(1)}$。而${\delta }_i^{(2)}$则是来自第 $2$ 层第 $i$ 个神经元的反向传播误差。

代入具体数字看看，如果$i=1,j=4$，则${\mathbf{W}}_{14}^{(1)}={\delta }_1^{(2)}{\mathbf{h}}_4^{(1)}$，目标函数对权重 ${\mathbf{W}}_{14}^{(1)}$ 的梯度是来自同层同神经元的输出${\mathbf{h}}_4^{(1)}$与来自更深一层神经元（该神经元正是图中权重所指向的那个神经元）的反向传播误差${\delta }_1^{(2)}$的乘积。

神经网络示意图
花了这么大的功夫来计算目标函数对权重的梯度，是有原因的。为了达到最大化间隔的目标，用的方法就是梯度下降，通过多次迭代找到间隔最大的那个函数的点。那么，为什么要计算梯度呢？因为目标函数的梯度所指的方向就是这个函数值下降最快的方向。所以我们让权重按这这个方向步进，迭代更新自己的值。

又有问题来了，问什么是对权重的梯度？而不是对输入$\mathbf{x}$的梯度呢？因为我们要训练的网络是根据输入得到一个输出，这个输出可以告诉我们哪个词是命名实体（是Pairs，还是museums）。训练网络的本质，就是训练网络中各层的权重，权重确定了，网络也就确定了。

2、${\mathbf{\delta }}^{(k)}$ 的解释

这里需要注意：官方note3文档中并没有解释什么是 ${\mathbf{\delta }}^{(k)}$，连公式推导中都只是一带而过，没有很清晰的解释。当然，网上随处都是 ${\mathbf{\delta }}^{(k)}$的解释，为了方便阅读，这里顺带提一下。首先计算目标函数对权重和偏置的梯度：
$$\begin{array}{rl}\frac{\partial s}{\partial {\mathbf{W}}_{ij}^{(k)}}& =\frac{\partial s}{\partial {\mathbf{z}}_i^{(k)}}\cdot \frac{\partial {\mathbf{z}}_i^{(k)}}{\partial {\mathbf{W}}_{ij}^{(k)}}={\delta }_i^{(k)}\cdot \frac{\partial {\mathbf{z}}_i^{(k)}}{\partial {\mathbf{W}}_{ij}^{(k)}}\\ \frac{\partial s}{\partial {\mathbf{b}}_i^{(k)}}& =\frac{\partial s}{\partial {\mathbf{z}}_i^{(k)}}\cdot \frac{\partial {\mathbf{z}}_i^{(k)}}{\partial {\mathbf{b}}_i^{(k)}}={\delta }_i^{(k)}\cdot \frac{\partial {\mathbf{z}}_i^{(k)}}{\partial {\mathbf{b}}_i^{(k)}}\end{array}$$
由于$\frac{\partial s}{\partial {\mathbf{z}}_i^{(k)}}$ 是两者都需要计算的相同部分，因此就把它叫做 ${\delta }_i^{(k)}$。

再来看，上面推导的一长串公式对 ${\delta }_i^{(k)}$ 的描述：${\delta }_i^{(2)}={\mathbf{W}}_i^{(2)}\cdot f^{\prime }\left({\mathbf{z}}_i^{(2)}\right)$，这两者一样吗？

当然一样，不信请看：$$\begin{array}{rl}{\delta }_i^{(2)}& =\frac{\partial s}{\partial {\mathbf{z}}_i^{(2)}}\\ & =\frac{\partial s}{\partial {\mathbf{h}}_j^{(2)}}\cdot \frac{\partial {\mathbf{h}}_j^{(2)}}{\partial {\mathbf{z}}_i^{(2)}}\\ & =\frac{\partial \left({\mathbf{W}}_i^{(2)}{\mathbf{h}}_i^{(2)}\right)}{\partial {\mathbf{h}}_j^{(2)}}\cdot \frac{\partial {\mathbf{h}}_j^{(2)}}{\partial {\mathbf{z}}_i^{(2)}}\\ & ={\mathbf{W}}_i^{(2)}\cdot \frac{\partial {\mathbf{h}}_j^{(2)}}{\partial {\mathbf{z}}_i^{(2)}}\\ & ={\mathbf{W}}_i^{(2)}\cdot f^{\prime }\left({\mathbf{z}}_i^{(2)}\right)\end{array}$$
这就对上号了。

3、权重梯度的反向传播

刚刚解释的是目标函数对权重的梯度长什么样，由哪些部分组成。那么，知道其组成之后，权重的梯度又是如何反向传播的呢？

这里单单把第2层的第1个神经元（用 $neura{l}_1^{(2)}$ 表示）拎出来，举例说明，如下图。

1. 首先假设我们有个误差信号（error signal）从 ${\mathbf{h}}_1^{(3)}$ 处开始反向传播，这个误差信号值为$\frac{\partial s}{\partial {\mathbf{h}}_1^{(3)}}=1$
2. 要穿过网络第3层神经元，需乘以该神经元的局部梯度（Local Gradient），即输出对输入的梯度：$$\frac{\partial {\mathbf{h}}_1^{(3)}}{\partial {\mathbf{z}}_1^{(3)}}=1$$所以来自第3层的误差信号值为 ${\delta }_1^{(3)}=1$
3. 误差信号继续往回传播。此时有两个回去的方向，一是 ${\mathbf{W}}_1^{(2)}$ ，二是 ${\mathbf{W}}_2^{(2)}$，我们考虑 $neura{l}_1^{(2)}$，因此选择 ${\mathbf{W}}_1^{(2)}$ 方向的路线，误差信号传播到 ${\mathbf{h}}_1^{(3)}$ 处需乘以该路线上的权重 ${\mathbf{W}}_1^{(2)}$ ，因此在 ${\mathbf{h}}_1^{(3)}$ 处的误差信号为 ${\mathbf{W}}_1^{(2)}{\delta }_1^{(3)}={\mathbf{W}}_1^{(2)}$
4. 与第2步相同，在误差信号穿过 $neura{l}_1^{(2)}$ 时，需乘以该神经元的局部梯度$$\frac{\partial {\mathbf{h}}_1^{(2)}}{\partial {\mathbf{z}}_1^{(2)}}=f^{\prime }\left({\mathbf{z}}_1^{(2)}\right)$$因此第二层的误差信号为 ${\delta }_1^{(2)}=f^{\prime }\left({\mathbf{z}}_1^{(2)}\right){\mathbf{W}}_1^{(2)}$
5. 误差信号再往回传播，若选择 ${\mathbf{W}}_{14}^{(1)}$ 方向，那么误差信号到达${\mathbf{h}}_4^{(1)}$时，其值为 ${\delta }_1^{(1)}={\mathbf{W}}_{14}^{(1)}{f}^{\prime }\left({\mathbf{z}}_1^{(2)}\right){\mathbf{W}}_1^{(2)}$

综上，可归纳为：
$$\begin{array}{rl}{\delta }_1^{(3)}& =1\\ {\delta }_1^{(2)}& =f^{\prime }\left({\mathbf{z}}_1^{(2)}\right){\mathbf{W}}_1^{(2)}{\delta }_1^{(3)}=f^{\prime }\left({\mathbf{z}}_1^{(2)}\right){\mathbf{W}}_1^{(2)}\\ {\delta }_1^{(1)}& ={\mathbf{W}}_{14}^{(1)}{\delta }_1^{(2)}={\mathbf{W}}_{14}^{(1)}{f}^{\prime }\left({\mathbf{z}}_1^{(2)}\right){\mathbf{W}}_1^{(2)}\end{array}$$

权重梯度反向传播示意图

4、${\mathbf{\delta }}^{(k+1)}$ 到${\mathbf{\delta }}^{(k)}$的传播

网络中的参数除了权重之外，偏置也是极其重要的部分，偏置的反向传播与权重类似，如下图。

权重梯度反向传播示意图

1. 误差信号 ${\delta }_i^{(k)}$ 从 ${\mathbf{z}}_i^{(k)}$ 开始反向传播，到达 ${\mathbf{h}}_i^{(k-1)}$ 时，误差信号变为： ${\delta }_i^{(k)}{\mathbf{W}}_{ij}^{(k-1)}$
2. 此时，考虑 $neura{l}_j^{(k-1)}$ 的输出流向多个下一层神经元，因此反向传播时就有多个误差信息同时流入该神经元，总的误差信号表示为 $$\sum _i{\delta }_i^{(k)}{\mathbf{W}}_{ij}^{(k-1)}$$
3. 在穿过 $neura{l}_j^{(k-1)}$ 后，误差信号要乘以该神经元的局部梯度，即有：$${\delta }_j^{(k-1)}=f^{\prime }\left({\mathbf{z}}_j^{k-1}\right)\sum _i{\delta }_i^{(k)}{\mathbf{W}}_{ij}^{(k-1)}\text{\hspace{1em}(1)}$$

根据公式(1)，可得到如下矩阵形式：
$$\begin{array}{rl}{\nabla }_{{\mathbf{W}}^{(k)}}& =\left[\begin{array}{cccc}& {\delta }_1^{(k+1)}{\mathbf{h}}_1^{(k)}& {\delta }_1^{(k+1)}{\mathbf{h}}_2^{(k)}& \cdots \\ & {\delta }_2^{(k+1)}{\mathbf{h}}_1^{(k)}& {\delta }_2^{(k+1)}{\mathbf{h}}_2^{(k)}& \cdots \\ & ⋮& ⋮& \ddots \end{array}\right]={\mathbf{\delta }}^{(k+1)}{\left({\mathbf{h}}^{(k)}\right)}^T\\ & \\ {\mathbf{\delta }}^{(k)}& =f^{\prime }\left({\mathbf{z}}^k\right)\circ \left({\left({\mathbf{W}}^{(k)}\right)}^T{\mathbf{\delta }}^{(k+1)}\right)\end{array}$$

5、偏置梯度

对于某个神经元来说，其输出对偏置的导数均为1，则可快速得到：$$\frac{\partial s}{\partial {\mathbf{b}}_i^{(k)}}={\delta }_i^{(k)}$$

五、Some Tips

详见官方note，这里不赘述。

Reference

1、2019斯坦福CS224n深度学习自然语言处理笔记（3）——分类模型与神经网络